Chuyển động tròn đều

Ta có:

+ Gia tốc hướng tâm: ${a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r$ (1)

+ Mặt khác, chu kì của chuyển động tròn: $T = \frac{{2\pi }}{\omega }$  (2)

Từ (1) và (2), ta suy ra: ${a_{ht}} = {\left( {\frac{{2\pi }}{T}} \right)^2}r \to T = 2\pi \sqrt {\frac{r}{{{a_{ht}}}}}  = 2\pi \sqrt {\frac{1}{{0,04}}}  = 10\pi s$

Ta có:

+ Chu kì của chuyển động: $T = 90.60 = 5400{\rm{s}}$

+ Tốc độ góc: $\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{5400}}\left( {ra{\rm{d}}/s} \right)$

+ Vận tốc dài: $v = \omega r = \frac{{2\pi }}{{5400}}.\left( {6380 + 320} \right).1000 = 7795,8\left( {m/s} \right)$

+ Ta có:

- Chu kì của kim giờ: ${T_h} = 12h = 12.60.60 = 43200{\rm{s}}$

- Chu kì của kim phút: ${T_m} = 60m = 60.60 = 3600{\rm{s}}$

+ Tốc độ góc của:

- Kim giờ: ${\omega _h} = \frac{{2\pi }}{{{T_h}}} = \frac{{2\pi }}{{43200}} = 1,{45.10^{ - 4}}\left( {ra{\rm{d}}/s} \right)$

- Kim phút: ${\omega _m} = \frac{{2\pi }}{{{T_m}}} = \frac{{2\pi }}{{3600}} = 1,{74.10^{ - 3}}\left( {ra{\rm{d/s}}} \right)$

Từ đầu bài ta có: Tốc độ góc $\omega  = 60$ vòng/phút $= 60.\frac{{2\pi }}{{60}} = 2\pi \left( {ra{\rm{d}}/s} \right)$

Mặt khác: $\omega  = \frac{{2\pi }}{T}$

Ta suy ra chu kì của hòn đá (thời gian hòn đá quay hết một vòng) $T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1{\rm{s}}$

Ta có:

+ Vận tốc dài và tốc độ góc:

$v = \omega r$

+ Tốc độ góc: $\omega  = \frac{{2\pi }}{T}$

+ Chu kì và tần số: $f = \frac{1}{T}$

Từ đây, ta suy ra các phương án:

B, C, D - đúng

A - sai vì: $f = \frac{1}{T} = \frac{\omega }{{2\pi }} = \frac{v}{{2\pi r}}$

Véctơ gia tốc của vật chuyển động tròn đều luôn vuông góc với véctơ vận tốc

Ta có:

+ Gia tốc hướng tâm: ${a_{ht}} = \frac{{{v^2}}}{r}$

+ Mặt khác, vận tốc dài: $v = \omega r$

+ Tốc độ góc: $\omega  = \frac{{2\pi }}{T}$

Ta suy ra:${a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r = {\left( {\frac{{2\pi }}{T}} \right)^2}r = 4{\pi ^2}\frac{r}{{{T^2}}}$

Ta có: Tốc độ góc: $\omega  = \dfrac{{2\pi }}{T} = 2\pi f$

Tốc độ góc tỉ lệ thuận với tần số và tỉ lệ nghịch với chu kì

=> Chuyển động nào có chu kì nhỏ hay tần số lớn thì tốc độ góc lớn và ngược lại, chuyển động nào có chu kì lớn hay tần số nhỏ thì tốc độ góc nhỏ.

Ta có:

+ Gia tốc hướng tâm: ${a_{ht}} = \frac{{{v^2}}}{r}$

+ Mặt khác, vận tốc dài: $v = \omega r$

Ta suy ra: ${a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r$

+ Ta có:

- Chu kì của kim giờ: ${T_g} = 12g = 12.60 = 720ph$

- Chu kì của kim phút: ${T_{ph}} = 60ph$

+ Vận tốc dài: $v = \omega r = \frac{{2\pi }}{T}r$

Ta suy ra, tỉ số: $\dfrac{{{v_{ph}}}}{{{v_g}}} = \dfrac{{\dfrac{{2\pi {r_{ph}}}}{{{T_{ph}}}}}}{{\dfrac{{2\pi {r_g}}}{{{T_g}}}}} = \dfrac{{{r_{ph}}{T_g}}}{{{r_g}{T_{ph}}}} = \dfrac{{4.720}}{{3.60}} = 16$

Ta có:

Vận tốc dài: $v = 40km/h = \frac{{100}}{9}m/s$

Gia tốc hướng tâm của xe: ${a_{ht}} = \frac{{{v^2}}}{r} = \frac{{{{\left( {\frac{{100}}{9}} \right)}^2}}}{{100}} = 1,23m/{s^2}$

A, B, C - đúng

D - sai vì véctơ vận tốc luôn thay đổi (thay đổi về hướng)

Ta có:

+ Chu kì của vật: $T = \frac{{2\pi }}{\omega }$

+ Mặt khác: $v = \omega r$

Ta suy ra: $T = \frac{{2\pi }}{v}r$

Theo đề bài, ta có chu kì của vật A và vật B là như nhau, ta suy ra:

$\begin{array}{l}\frac{{2\pi }}{{{v_A}}}{r_A} = \frac{{2\pi }}{{{v_B}}}{r_B} \leftrightarrow \frac{{{r_A}}}{{{v_A}}} = \frac{{{r_B}}}{{{v_B}}}\\ \to {v_B} = \frac{{{r_B}}}{{{r_A}}}{v_A} = \frac{1}{4}{v_A} = \frac{{12}}{4} = 3m/s\end{array}$

Ta có:

+ Vận tốc dài và vận tốc góc liên hệ với nhau theo biểu thức: $v = \omega r$  (1)

+ Gia tốc hướng tâm của vật: ${a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r$ (2)

Từ (1) và (2), ta suy ra: ${a_{ht}} = v\omega  = 5.10 = 50m/{s^2}$

Chu kì của kim phút là : $T = 1h = 3600s$

Tần số của kim phút là : $f = \dfrac{1}{T} = \dfrac{1}{{3600}}{s^{ - 1}}$

R₁ = 15cm; R₂ = 20cm

Chu kì của kim giờ: T₂ = 12h = 43200s

Chu kì của kim phút: T₂ = 1h = 3600s

Tốc độ góc: $\left\{ \begin{array}{l}{\omega _1} = \dfrac{{2\pi }}{{{T_1}}} \approx 1,{454.10^{ - 4}}\,\,rad/s\\{\omega _2} = \dfrac{{2\pi }}{{{T_2}}} \approx 1,{744.10^{ - 3}}\,\,rad/s\end{array} \right.$

Lúc 12h hai kim trùng nhau.

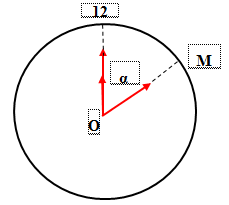
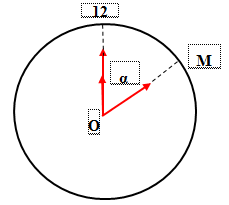
Ta có: ${\alpha _2} - {\alpha _1} = 2\pi  \Leftrightarrow {\omega _2}t - {\omega _1}t = 2\pi  \Rightarrow t = \dfrac{{2\pi }}{{{\omega _2} - {\omega _1}}} \approx 3928s \approx 1h5ph28s$

v_A = 50cm/s; v_B = 10cm/s; AB = 20cm.

a) Ta có: $\left\{ \begin{array}{l}{v_A} = {R_A}.\omega \\{v_B} = {R_B}.\omega \\{R_A} - {R_B} = AB\end{array} \right. \Rightarrow {v_A} - {v_B} = \left( {{R_A} - {R_B}} \right)\omega  \Rightarrow \omega  = \dfrac{{{v_A} - {v_B}}}{{{R_A} - {R_B}}} = \dfrac{{50 - 10}}{{20}} = 2rad/s$

$\Rightarrow \left\{ \begin{array}{l}{R_A} = \dfrac{{{v_A}}}{\omega } = \dfrac{{50}}{2} = 25cm\\{R_B} = \dfrac{{{v_B}}}{\omega } = \dfrac{{10}}{2} = 5cm\end{array} \right.$

→ Gia tốc hướng tâm: $\left\{ \begin{array}{l}{a_A} = {R_A}{\omega ^2} = 100cm/{s^2}\\{a_B} = {R_B}{\omega ^2} = 20cm/{s^2}\end{array} \right.$

A và B có cùng tốc độ góc ω. Gọi r_A ; r_B là bán kính quỹ đạo chuyển động tròn đều của A và B.

Ta có: ${r_A} - {r_B} = 20cm\,\,\,\,\left( 1 \right)$

Tốc độ dài của A và B là $\left\{ \begin{array}{l}{v_A} = \omega {r_A} = 60cm/s\\{v_B} = \omega {r_B} = 20cm/s\end{array} \right. \Rightarrow {r_A} = 3{r_B}\,\,\,\,\left( 2 \right)$

Từ (1) và (2) $\Rightarrow {r_A} = 30cm \Rightarrow \omega  = \dfrac{{{v_A}}}{{{r_A}}} = \dfrac{{60}}{{30}} = 2rad/s$

Cách giải:

Bán kính của Trái Đất là: R = 6400 km = 6400 000 m

Coi chuyển động của tàu thủy neo tại một điểm trên đường xích đạo là chuyển động tròn đều với bán kính là bán kính Trái Đất và tâm là tâm Trái Đất.

Trái Đất quay quanh trục của nó được một vòng mất 24h  → Chu kì quay của 1 điểm nằm trên đường xích đạo quanh trục Trái Đất là:

T = 24h = 24.3600 = 86400s

Tốc độ góc của tàu đối với trục quay của Trái Đất là:

$\omega  = \frac{{2\pi }}{T} = \frac{{2.3,14}}{{86400}} = 7,{269.10^{ - 5}}\,rad/s$

Tốc độ dài của tàu đối với trục quay của Trái Đất là:

$v = \omega .r = 7,{269.10^{ - 5}}.6400000 = 465,216m/s$

Ta có:

+ Tốc độ góc $\omega  = 2\pi rad/s$

$\Rightarrow$ Chu kì: $T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1s$

Tần số $f = \dfrac{1}{T} = \dfrac{1}{1} = 1Hz$

+ Tốc độ dài của một điểm thuộc vành ngoài bánh xe:

$v = \omega r = 2\pi .30 \approx 189,74cm/s$

+ Gia tốc hướng tâm của một điểm thuộc vành ngoài bánh xe:

${a_{ht}} = {\omega ^2}r = {\left( {2\pi } \right)^2}.0,3 = 12m/{s^2}$