Đặc điểm của hệ ba lực cân bằng là
Điều kiện cân bằng của một vật chịu tác dụng của ba lực không song song:
- Ba lực đó phải có giá đồng phẳng và đồng quy
- Hợp lực của hai lực phải cân bằng với lực thứ ba
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = - \overrightarrow {{F_3}} \) hay \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
Vật rắn có khối lượng 200g nằm cân bằng trên mặt phẳng nghiêng góc \(\alpha = {60^0}\). Lực căng dây có giá trị là bao nhiêu? Lấy \(g = 9,8m/{s^2}\) và bỏ qua ma sát.


Ta có,
+ Các lực tác dụng lên vật gồm:trọng lực P, lực căng dây T, phản lực N
+ Áp dụng điều kiện cân bằng của vật rắn, ta có: \(\overrightarrow P + \overrightarrow T + \overrightarrow N = \overrightarrow 0 \)(1)
+ Gắn hệ trục tọa độ như hình vẽ, chiếu (1) theo phương Ox, ta được:
\(T - {P_x} = 0 \\\to T = {P_x} = P\sin \alpha = mg\sin \alpha \\= 0,2.9,8.\sin {60^0} = 1,7N\)
Một thanh đồng chất nằm cân bằng ở tư thế nằm ngang bởi hai sợi dây buộc vào hai đầu của nó như hình.
Lực căng dây có độ lớn \({T_1} = {T_2} = 10N\), góc \(\theta = {37^0}\). Trọng lượng của thanh bằng

+ Áp dụng điều kiện cân bằng của vật rắn dưới tác dụng của 3 lực không song song, ta có:
\(\overrightarrow P + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow 0 \)

Chiếu lên trục Oy, ta được:
\({T_{1y}} + {T_{2y}} - P = 0\)
\(\begin{array}{l} \Rightarrow P = {T_{1y}} + {T_{2y}} = {T_1}\sin \theta + {T_2}\sin \theta \\ = 2T.\sin \theta = 2.10.\sin {37^0} \approx 12N\end{array}\)
Một quả cầu đồng chất có khối lượng \(4kg\) được treo vào tường thẳng đứng nhờ một sợi dây hợp với tường một góc \(\alpha = {30^0}\). Bỏ qua ma sát ở chỗ tiếp xúc của quả cầu với tường. Lấy \(g = 9,8m/{s^2}\). Lực của quả cầu tác dụng lên tường có độ lớn

+ Các lực tác dụng lên vật gồm: trọng lực P, lực căng dây T và phản lực N của mặt phẳng thẳng đứng
+ Vận dụng điều kiện cân bằng của vật rắn, ta có: \(\overrightarrow P + \overrightarrow T + \overrightarrow N = \overrightarrow 0 \) (1)
+ Chọn hệ trục Oxy như hình, chiếu (1) theo các phương, ta được:
- Ox: \(T\sin \alpha - N = 0 \to N = T\sin \alpha \)(2)
- Oy: \( - P + Tc{\rm{os}}\alpha = 0 \to T = \dfrac{P}{{{\rm{cos}}\alpha }}\)(3)
Từ (2) và (3), ta suy ra:
\(\begin{array}{l}N = P\dfrac{{\sin \alpha }}{{{\rm{cos}}\alpha }} = P\tan \alpha \\ = mg.\tan {30^0} = 4.9,8.\tan {30^0} = 22,63N\end{array}\)
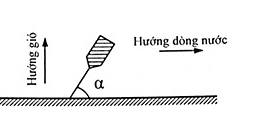
Một chiếc thuyền nằm trên bờ sông như hình vẽ. Biết \(\alpha = {30^0}\), lực căng của dây \(T = 50N\). Lực do gió và nước tác dụng lên thuyền có giá trị:

Ta có:
+ Các lực tác dụng lên thuyền gồm: Lực gió \(\overrightarrow {{F_g}} \), lực nước \(\overrightarrow {{F_n}} \), lực căng dây \(\overrightarrow T \) , trọng lực \(\overrightarrow P \)và lực đẩy acsimét \(\overrightarrow {{F_A}} \)
Ta có, trọng lực P và lực đẩy acsimét cân bằng với nhau.
+ Áp dụng điều kiện cân bằng của vật rắn, ta có: \(\overrightarrow {{F_g}} + \overrightarrow {{F_n}} + \overrightarrow T = \overrightarrow 0 \)(1)
(do \(\overrightarrow P + \overrightarrow {{F_A}} = \overrightarrow 0 \)nên ta bỏ hai lực này ra khỏi điều kiện)
=>Lực gió và lực nước cân bằng với lực căng dây T
Từ hình, ta suy ra:
\(\left\{ \begin{array}{l}{F_n} = Tc{\rm{os}}\alpha = 50.c{\rm{os3}}{{\rm{0}}^0} = 25\sqrt 3 N\\{F_g} = T\sin \alpha = 50.\sin {30^0} = 25N\end{array} \right.\)
Vật nặng \(m = 2kg\) chuyển động thẳng đều trên mặt phẳng ngang nhờ hai dây kéo nằm trong mặt phẳng ngang và hợp với nhau góc \(\alpha = {30^0}\) không đổi. Lực kéo đặt vào mỗi dây là \(F = 10N\), lấy \(g = 10m/{s^2}\). Lực ma sát giữa vật và mặt phẳng ngang có giá trị là:
Ta có, các lực tác dụng lên vật được biểu diễn trong hình
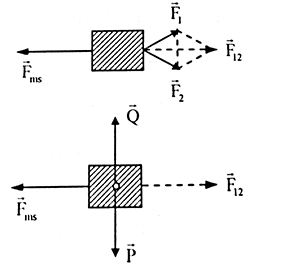
+ Mặt khác, vật chuyển động thẳng đều khi tổng hợp lực tác dụng lên vật bằng 0
ta suy ra: \(\overrightarrow {{F_{m{\rm{s}}}}} + \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow P + \overrightarrow Q = \overrightarrow 0 \)(1)
Chiếu (1) ta được:
- \(Q = P\)
- \({F_{12}} = {F_{m{\rm{s}}}}\)
Ta có, \({F_1} = {F_2} = F \to {F_{12}} = 2Fc{\rm{os}}\dfrac{\alpha }{2}\)
Ta suy ra:\({F_{m{\rm{s}}}} = 2Fc{\rm{os}}\dfrac{\alpha }{2} = 2.10.c{\rm{os}}\dfrac{{{{30}^0}}}{2} = 19,32N\)
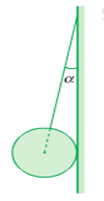
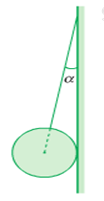
Một quả cầu đồng chất có khối lượng 3kg được treo vào tường nhờ một sợi dây. Dây làm với tường một góc \(\alpha = {20^0}\) (hình vẽ). Bỏ qua ma sát chỗ tiếp xúc của quả cầu với tường.
Lấy g = 10m/s2. Lực căng T của dây là :
Ta có: \(m = 3kg;\;g = 9,8{\rm{ }}m/{s^2};\alpha = {20^0}\)
Lực tác dụng lên quả cầu được biểu diễn trên hình vẽ:
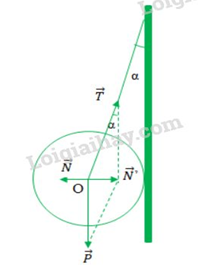
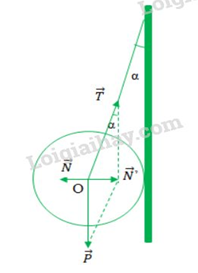
Khi hệ cân bằng ta có: \(\overrightarrow P + \overrightarrow T + \overrightarrow N = \overrightarrow 0 \, \Leftrightarrow \overrightarrow P + \overrightarrow T = - \overrightarrow N \Leftrightarrow \overrightarrow P + \overrightarrow T = \overrightarrow {N'} \)
Xét tam giác N’OT vuông tại N’ ta có :
\(\cos \alpha = \dfrac{P}{T} \Rightarrow T = \dfrac{P}{{\cos \alpha }} = \dfrac{{mg}}{{\cos \alpha }} = \dfrac{{3.10}}{{\cos 20}} = 31,92N\)
Một vật có khối lượng m = 2kg được giữ yên trên một mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính (Hình 17.9). Biết góc nghiêng α = 30o, g = 9,8 m/s2 và ma sát là không đáng kể. Hãy xác định phản lực của mặt phẳng nghiêng lên vật?
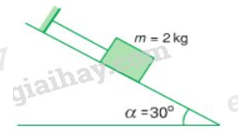

Các lực tác dụng lên vật gồm: trọng lực \(\overrightarrow P \); phản lực \(\overrightarrow N \) và lực căng dây \(\overrightarrow T \)
Biểu diễn các lực tác dụng lên vật và chọn hệ trục toạ độ Oxy như hình vẽ:
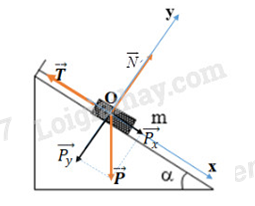

Khi vật cân bằng ta có: \(\overrightarrow P + \overrightarrow N + \overrightarrow T = \overrightarrow 0 \,\,\,\,\,\left( 1 \right)\)
Chiếu (1) theo lên các trục Ox và Oy ta được: \(\left\{ \begin{array}{l}P.\sin \alpha - T = 0\,\,\,\,\,\,\,\left( 2 \right)\\ - P.\cos \alpha + N = 0\,\,\,\,\left( 3 \right)\end{array} \right.\)
Từ (3) \( \Rightarrow N = P.\cos \alpha = 2.9,8.\cos 30 = 16,97N\)
Một quả cầu có trọng lượng P = 40N được treo vào tường nhờ một sợi dây hợp với mặt tường một góc α = 30o. Bỏ qua ma sát ở chỗ tiếp xúc giữa quả cầu và tường. Hãy xác định lực căng của dây và phản lực của tường tác dụng lên quả cầu (hình vẽ):
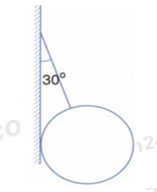

Quả cầu chịu tác dụng của 3 lực: Trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \) và lực căng \(\overrightarrow T \)
Khi quả cầu nằm cân bằng ta có: \(\overrightarrow P + \overrightarrow T + \overrightarrow N = \overrightarrow 0 \, \Leftrightarrow \overrightarrow P + \overrightarrow N = - \overrightarrow T \Leftrightarrow \overrightarrow P + \overrightarrow N = \overrightarrow {T'} \)

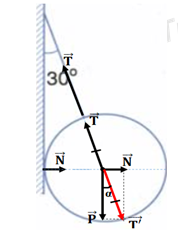
Từ hình vẽ ta có: \(\cos \alpha = \dfrac{P}{{T'}} \Rightarrow T' = \dfrac{P}{{\cos \alpha }} = \dfrac{{40}}{{\cos 30}} \approx 46,2N\)
Vì T = T’ nên lực căng của dây là 46,2N
Phản lực của tường tác dụng lên quả cầu: \(N = P.tan\alpha = 40.tan{30^0} = 23,1N\)
Phát biểu nào sau đây là đúng khi nói về quy tắc tổng hợp hai lực đồng quy?
Quy tắc hợp 2 lực đồng quy: Trượt hai lực trên giá của chúng đến điểm đồng quy rồi áp dụng quy tắc hình bình hành để tìm hợp lực của hai lực đồng quy.
Điều kiện cân bằng của vật chịu tác dụng của ba lực đó có giá đồng phẳng và đồng quy không song song là :
Điều kiện cân bằng của vật chịu tác dụng của ba lực đó có giá đồng phẳng và đồng quy không song song là: - Ba lực đó phải có giá đồng phẳng và đồng quy
- Hợp lực của hai lực phải cân bằng với lực thứ ba: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = - \overrightarrow {{F_3}} \) hay \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
Ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) tác dụng lên cùng một vật rắn giữ cho vật cân bằng. Vật tiếp tục cân bằng nếu
Ta có: Tác dụng của một lực lên một vật rắn không thay đổi khi điểm đặt của lực đó dời chỗ trên giá của nó
=> Ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) tác dụng lên cùng một vật rắn giữ cho vật cân bằng. Vật tiếp tục cân bằng nếu di chuyển điểm đặt của một lực trên giá của nó.
Điều kiện cân bằng của một vật chịu tác dụng của ba lực không song song là: Ba lực đó phải có giá đồng phẳng, đồng quy và thoả mãn điều kiện:
Điều kiện cân bằng của một vật chịu tác dụng của ba lực không song song:
- Ba lực đó phải có giá đồng phẳng và đồng quy
- Hợp lực của hai lực phải cân bằng với lực thứ ba:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = - \overrightarrow {{F_3}} \) hay \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
Cho vật cân bằng dưới tác dụng của 3 lực như hình vẽ. Phát biểu nào sau đây không đúng?
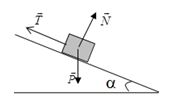
Khi vật cân bằng, ta có: \(\overrightarrow P + \overrightarrow N + \overrightarrow T = \overrightarrow 0 \)
A, B, D - đúng
C - sai vì: \(\overrightarrow N \) cân bằng với \(\overrightarrow {{P_y}} \) và: \(N = {P_y} = Pc{\rm{os}}\alpha = mgc{\rm{os}}\alpha \)
Vật rắn có khối lượng $2kg$ nằm cân bằng trên mặt phẳng nghiêng góc \(\alpha = {30^0}\). Lực căng dây có giá trị là bao nhiêu? Lấy \(g = 9,8m/{s^2}\) và bỏ qua ma sát.
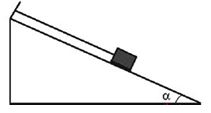

Ta có,
+ Các lực tác dụng lên vật gồm: trọng lực P, lực căng dây T, phản lực N
+ Áp dụng điều kiện cân bằng của vật rắn, ta có: \(\overrightarrow P + \overrightarrow T + \overrightarrow N = \overrightarrow 0 \) (1)
+ Gắn hệ trục tọa độ như hình vẽ, chiếu (1) theo phương Ox, ta được:
\(-T + {P_x} = 0 \to T = {P_x} = P\sin \alpha = mg\sin \alpha = 2.9,8.\sin {30^0} = 9,8N\)
Một diễn viên xiếc (coi là một vật rắn) có trọng lượng 800N đi xe đạp một bánh trên dây làm dây võng xuống một góc \({120^0}\). Lực căng của dây treo có giá trị là bao nhiêu khi diễn viên xiếc đứng cân bằng? Coi dây không giãn.
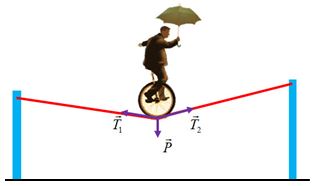
+ Áp dụng điều kiện cân bằng của vật rắn dưới tác dụng của 3 lực không song song, ta có:
\(\overrightarrow P + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow 0 \)
Từ hình, ta có: \({P^2} = T_1^2 + T_2^2 + 2{T_1}{T_2}{\rm{cos12}}{{\rm{0}}^0} = T_1^2 + T_2^2 - {T_1}{T_2}\) (1)
+ Mặt khác, do dây không giãn, ta suy ra: \({T_1} = {T_2}\) (2)
Từ (1) và (2), ta suy ra: \({T_1} = {T_2} = P = 800N\)
Vật rắn có khối lượng 5kg được treo cân bằng trên mặt phẳng thẳng đứng bằng một sợi dây như hình vẽ. Bỏ qua ma sát, lấy \(g = 9,8m/{s^2}\), góc \(\alpha = {20^0}\). Phản lực N của mặt phẳng thẳng đứng có giá trị là:


+ Các lực tác dụng lên vật gồm: trọng lực P, lực căng dây T và phản lực N của mặt phẳng thẳng đứng
+ Vận dụng điều kiện cân bằng của vật rắn, ta có: \[\overrightarrow P + \overrightarrow T + \overrightarrow N = \overrightarrow 0 \] (1)
+ Chọn hệ trục Oxy như hình, chiếu (1) theo các phương, ta được:
- Ox: \(T\sin \alpha - N = 0 \to N = T\sin \alpha \)(2)
- Oy: \( - P + Tc{\rm{os}}\alpha = 0 \to T = \frac{P}{{{\rm{cos}}\alpha }}\)(3)
Từ (2) và (3), ta suy ra:
\(\begin{array}{l}N = P\frac{{\sin \alpha }}{{{\rm{cos}}\alpha }} = P\tan \alpha \\ = mg.\tan {20^0} = 5.9,8.\tan {20^0} = 17,8N\end{array}\)
Một chiếc thuyền nằm trên bờ sông như hình vẽ. Biết \(\alpha = {60^0}\), lực căng của dây \(T = 100N\). Lực do gió và nước tác dụng lên thuyền có giá trị:
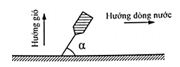

Ta có:
+ Các lực tác dụng lên thuyền gồm: Lực gió \(\overrightarrow {{F_g}} \), lực nước \(\overrightarrow {{F_n}} \), lực căng dây \(\overrightarrow T \) , trọng lực \(\overrightarrow P \)và lực đẩy acsimét \(\overrightarrow {{F_A}} \)
Ta có, trọng lực P và lực đẩy acsimét cân bằng với nhau.
+ Áp dụng điều kiện cân bằng của vật rắn, ta có: \(\overrightarrow {{F_g}} + \overrightarrow {{F_n}} + \overrightarrow T = \overrightarrow 0 \)(1)
(do \(\overrightarrow P + \overrightarrow {{F_A}} = \overrightarrow 0 \)nên ta bỏ hai lực này ra khỏi điều kiện)
=>Lực gió và lực nước cân bằng với lực căng dây T
Từ hình, ta suy ra:
\(\left\{ \begin{array}{l}{F_n} = Tc{\rm{os}}\alpha = 100.c{\rm{os6}}{{\rm{0}}^0} = 50N\\{F_g} = T\sin \alpha = 100.\sin {60^0} = 50\sqrt 3 \end{array} \right.\)
Vật nặng \(m = 2,5kg\) chuyển động thẳng đều trên mặt phẳng ngang nhờ hai dây kéo nằm trong mặt phẳng ngang và hợp với nhau góc \(\alpha = {60^0}\) không đổi. Lực kéo đặt vào mỗi dây là \(F = 10N\), lấy \(g = 9,8m/{s^2}\). Hệ số ma sát giữa vật và mặt phẳng ngang có giá trị là:
Ta có, các lực tác dụng lên vật được biểu diễn trong hình
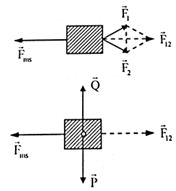
+ Mặt khác, vật chuyển động thẳng đều khi tổng hợp lực tác dụng lên vật bằng 0
ta suy ra: \[\overrightarrow {{F_{m{\rm{s}}}}} + \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow P + \overrightarrow Q = \overrightarrow 0 \](1)
Chiếu (1) ta được:
- \(Q = P\)
- \({F_{12}} = {F_{m{\rm{s}}}}\)
Ta có, \({F_1} = {F_2} = F \to {F_{12}} = 2Fc{\rm{os}}\frac{\alpha }{2}\)
Ta suy ra: \({F_{m{\rm{s}}}} = 2Fc{\rm{os}}\frac{\alpha }{2} = 2.10.c{\rm{os}}\frac{{{{60}^0}}}{2} = 10\sqrt 3 N\)
Ta lại có:
\(\begin{array}{l}{F_{m{\rm{s}}}} = \mu mg = 10\sqrt 3 N\\ \to \mu = \frac{{10\sqrt 3 }}{{2,5.9,8}} \approx 0,71\end{array}\)
Hai mặt phẳng đỡ tạo với mặt phẳng nằm ngang các góc α = 45o . Trên hai mặt phẳng đó người ta đặt một quả cầu đồng chất có khối lượng 2 kg (Hình 17.10). Bỏ qua ma sát và lấy g = 10 m/s2. Hỏi áp lực của quả cầu lên mỗi mặt phẳng đỡ bằng bao nhiêu?
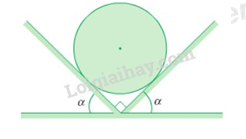
Lực tác dụng lên quả cầu được biểu diễn như hình vẽ.

Khi hệ cân bằng ta có: \(\overrightarrow P + \overrightarrow {{N_1}} + \overrightarrow {{N_2}} = \overrightarrow 0 \,\,\,\,\left( 1 \right)\)
Chọn hệ trục toạ độ Oxy như hình vẽ.
Chiếu phương trình (1) lên các trục Ox, Oy ta có :
\(\begin{array}{l}\left\{ \begin{array}{l}{N_1}.\cos \alpha - {N_2}.\cos \alpha = 0\\ - P + {N_1}.\sin \alpha + {N_2}.\sin \alpha = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{N_1} = {N_2}\\P = {N_1}.\sin \alpha + {N_2}.\sin \alpha \end{array} \right. \Rightarrow P = 2{N_1}\sin \alpha \\ \Rightarrow {N_1} = \dfrac{P}{{2\sin \alpha }} = \dfrac{{mg}}{{2\sin \alpha }} = \dfrac{{2.10}}{{2.\sin 45}} \approx 14N \Rightarrow {N_1} = {N_2} = 14N\end{array}\)

