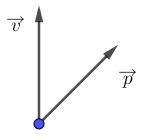
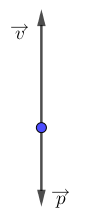
Một chất điểm chuyển động theo phương thẳng đứng, hướng lên. Hình nào sau đây biểu diễn đúng quan hệ giữa \(\overrightarrow v \) và \(\overrightarrow p \) của chất điểm đó
Ta có: \(\overrightarrow p = m\overrightarrow v \)
\( \to \overrightarrow p \uparrow \uparrow \overrightarrow v \)
(Động lượng của vật cùng phương, cùng chiều với vận tốc của vật)
Phát biểu nào sau đây đúng?
A – sai vì: Động lượng của một vật bằng tích khối lượng và vận tốc của vật.
B – sai vì: Động lượng của một vật là một đại lượng vectơ.
C - sai vì: Đơn vị của động lượng là \(kg.m/s\) hoặc \(N.s\)còn đơn vị của năng lượng là J
D - đúng
Một vật có khối lượng \(450g\) chuyển động thẳng dọc trục Ox với vận tốc \(72km/h\). Động lượng của vật bằng:
Ta có: \(72km/h = 20m/s\)
Động lượng của vật: \(\overrightarrow p = m\overrightarrow v \)
Xét về độ lớn: \(p = mv = 0,45.20 = 9kg.m/s\)
Tìm phát biểu không đúng.
Độ lớn động lượng của vật không đổi khi vật
Ta có, độ lớn động lượng của vật \(p = mv\)
=> Độ lớn động lượng của một vật không thay đổi khi vật đó chuyển động với vận tốc không đổi
Các phương án B, C, D độ lớn vận tốc của vật không đổi => Độ lớn động lượng của vật không đổi
Phương án A – vận tốc của vật thay đổi \(\left( {v = {v_0} + at} \right)\) => Độ lớn động lượng của vật thay đổi
Độ biến thiên động lượng \(\Delta \overrightarrow p \) của vật
Ta có: Độ biến thiên động lượng của một vật trong một khoảng thời gian nào đó bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó.
\(\overrightarrow {{p_2}} - \overrightarrow {{p_1}} = \Delta \overrightarrow p = \overrightarrow F \Delta t\)
Một chất điểm chuyển động không vận tốc đầu dưới tác dụng của lực không đổi \(F = 0,25N\). Động lượng chất điểm ở thời điểm \(t = 4s\) kể từ lúc bắt đầu chuyển động là:
Ta có: Độ biến thiên động lượng của một vật trong một khoảng thời gian nào đó bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó.
\(\overrightarrow {{p_2}} - \overrightarrow {{p_1}} = \Delta \overrightarrow p = \overrightarrow F \Delta t\)
Ta có: Do vật chuyển động không vận tốc đầu nên: \(\overrightarrow {{p_1}} = \overrightarrow 0 \)
\(\Delta \overrightarrow p = \overrightarrow {{p_2}} = \overrightarrow F t\)
Xét về độ lớn, ta có: \({p_2} = F.t = 0,25.4 = 1N.s = 1kg.m/s\)

Hình trên là đồ thị tọa độ – thời gian của một vật có khối lượng \(12kg\). Động lượng của vật tại thời điểm \({t_1} = 2s\) và thời điểm \({t_2} = 6s\) lần lượt bằng:
Từ đồ thị ta có:
+ Thời điểm ban đầu \(t{\rm{ }} = {\rm{ }}0\) đến thời điểm \(t{\rm{ }} = {\rm{ }}3{\rm{ }}s\), vật chuyển động thẳng đều với vận tốc bằng \({v_1} = \dfrac{{\Delta x}}{{\Delta t}} = \dfrac{{60 - 0}}{{3 - 0}} = 20cm/s = 0,2m/s\)
+ Từ thời điểm \(t{\rm{ }} = {\rm{ }}3{\rm{ }}s\) trở về sau vật đứng yên không chuyển động \({v_2} = 0m/s\)
Tại thời điểm \({t_1} = 2s\) nằm trong khoảng thời gian từ \(0 \Rightarrow 3s\)
=> Lúc này vận tốc của vật là \({v_1}\)
=> Động lượng tại thời điểm này: \({p_1} = m{v_1} = 12.0,2 = 2,4kg.m/s\)
Tại thời điểm \({t_2} = 6s\) thuộc phần sau của chuyển động
=> Lúc này vật đứng yên \({v_2} = 0m/s\)
=> Động lượng tại thời điểm này: \({p_2} = m{v_2} = 0kg.m/s\)
Một vật \(250g\) rơi tự do không vận tốc đầu xuống đất trong khoảng thời gian \(2s\). Độ biến thiên động lượng của vật trong khoảng thời gian đó là? (lấy \(g{\rm{ }} = {\rm{ }}9,8{\rm{ }}m/{s^2}\)).
Xung lượng của trọng lực bằng độ biến thiên động lượng của vật:
\( \Rightarrow \Delta p = F.\Delta t\)
Ta có: \(F\) - ở đây chính là trọng lượng của vật \(P = mg\)
\( \Rightarrow \Delta p = P.\Delta t = mg.\Delta t = 0,25.9,8.2 = 4,9kg.m/s\)
Vật có khối lượng \({m_1}\; = 3kg\) đang chuyển động đều với vận tốc \({v_1}\; = 5m/s\)đến va chạm với vật \({m_2}\; = 2kg\) đang đứng yên. Sau va chạm hai vật dính vào nhau và chuyển động cùng vận tốc. Độ lớn vận tốc hai vật sau va chạm là:
+ Trước va chạm:
Vật 1: \({m_1}\; = 3kg;{v_1}\; = 5m/s\)
Vật 2: \({m_2}\; = 2kg;{v_2}\; = 0\) (do vật 2 đang đứng yên)
+ Sau va chạm:
Hai vật dính vào nhau nên:
\(m = {m_1} + {m_2}\; = 3 + 2 = 5kg\)
Sau va chạm hai vật chuyển động với cùng vận tốc là \(V\)
+ Áp dụng định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_{trc}}} = \overrightarrow {{p_{sau}}} \)
\(\begin{array}{l} \Rightarrow {m_1}{v_1} + {m_2}{v_2} = mV\\ \Leftrightarrow 3.5 + 2.0 = 5.V \Leftrightarrow V = \dfrac{{3.5}}{5} = 3m/s\end{array}\)
Một quả bóng có khối lượng \(500g\) đang bay theo phương ngang với vận tốc \(20m/s\) thì tới đập vào tường thẳng đứng và bật ngược trở lại theo đúng phương cũ với vận tốc có độ lớn như cũ. Độ biến thiên động lượng của quả bóng bằng
Chọn chiều dương là chiều chuyển động của quả bóng sau khi đập vào tường
Ta có:
+ Trước khi đập vào tường, động lượng của quả bóng: \({p_1} = - m{v_1} = - 0,5.20 = - 10kg.m/s\)
+ Sau khi đập vào tường, động lượng của quả bóng: \({p_2} = m{v_2} = 0,5.20 = 10kg.m/s\)
Độ biến thiên động lượng \(\Delta p = {p_2} - {p_1} = 10 - \left( { - 10} \right) = 20kg.m/s\)
Một vật nhỏ trọng lượng \(2N\) rơi tự do. Độ biến thiên động lượng của vật trong 1 giây đầu tiên bằng
Trọng lượng của vật:
\(P = mg = m.10 = 2N \Rightarrow m = 0,2kg\)
Độ biến thiên động lượng:
\(\Delta p = {p_2} - {p_1} = m.\left( {{v_2} - {v_1}} \right)\)
Vật rơi tự do nên: \(\left\{ \begin{array}{l}{v_1} = 0\\{v_2} = gt = 10.1 = 10\;m/s\end{array} \right.\)
\( \Rightarrow \Delta p = m{v_2} = 0,2.10 = 2kg.m/s\)
Một quả bóng khối lượng \(0,5kg\) đang nằm yên thì được đá cho nó chuyển động vói vận tốc \(25m/s\). Xung lượng của lực tác dụng lên quả bóng bằng
Ta có: Xung lượng của lực bằng độ biến thiên động lượng \(\overrightarrow F \Delta t = \Delta \overrightarrow p \)
+ Ban đầu quả bóng đứng yên: \( \Rightarrow {p_1} = 0\)
+ Sau khi đá, quả bóng có vận tốc \(v = 25m/s\) \( \Rightarrow {p_2} = mv = 0,5.25 = 12,5kg.m/s\)
Ta suy ra xung lượng của lực: \(F.\Delta t = \Delta p = {p_2} - {p_1} = 12,5 - 0 = 12,5kg.m/s = 12,5N.s\)
Véctơ động lượng là véctơ:
Vecto động lượng là vecto cùng phương, cùng chiều với vecto vận tốc.
Một viên đạn có khối lượng \(10g\) chuyển động với vận tốc \(1000m/s\) xuyên qua tấm gỗ. Sau đó vận tốc của viên đạn là \(500m/s\), thời gian viên đạn xuyên qua tấm gỗ là \(0,01s\). Lực cản trung bình của tấm gỗ là
+ Động lượng của viên đạn trước khi đâm vào tấm gỗ là: \({p_1} = m{v_1} = 0,01.1000 = 10kg.m/s\)
+ Động lượng của viên đạn sau khi xuyên qua tấm gỗ là: \({p_2} = m{v_2} = 0,01.500 = 5kg.m/s\)
=> Biến thiên động lượng của viên đạn: \(\Delta p = {p_2} - {p_1} = 5 - 10 = - 5kg.m/s\)
+ Mặt khác, ta có: Xung lượng của lực cản của tấm gỗ \({F_c}.\Delta t = \Delta p\)
=> Lực cản trung bình: \({F_c} = \dfrac{{\Delta p}}{{\Delta t}} = \dfrac{{ - 5}}{{0,01}} = - 500N\)
Một hệ gồm hai vật có khối lượng và độ lớn vận tốc lần lượt là \({m_1} = 2kg,{v_1} = 3m/s\) và \({m_2} = 1kg,{v_2} = 6m/s\). Tìm tổng động lượng của hệ trong các trường hợp:
a) Hai vật chuyển động theo hai hướng hợp với nhau góc \(\alpha = {60^0}\)
b) Hai vật chuyển động theo hai hướng hợp với nhau góc \(\alpha = {120^0}\)
Ta có: \(\left\{ \begin{array}{l}{m_1} = 2kg;{v_1} = 3m/s\\{m_2} = 1kg;{v_2} = 6m/s\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{p_1} = {m_1}{v_1} = 6kg.m/s\\{p_2} = {m_2}{v_2} = 6kg.m/s\end{array} \right.\)
Tổng động lượng: \(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
a) Với \(\alpha = {60^0}\)
\(\begin{array}{l} \Rightarrow p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \alpha } \\\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{6^2} + {6^2} + 2.6.6.cos60} = 6\sqrt 3 kg.m/s\end{array}\)
b) Với \(\alpha = {120^0}\)
\(\begin{array}{l} \Rightarrow p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \alpha } \\\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{6^2} + {6^2} + 2.6.6.cos120} = 6kg.m/s\end{array}\)
Hai vật chuyển động trên mặt phẳng ngang, xác định động lượng của hệ vật trong trường hợp hai vật chuyển động hợp với nhau một góc vuông. Biết khối lượng và vận tốc của các vật lần lượt là \(400g\) và \(200g\), \(6m/s\) và \(12m/s\).
Ta có động lượng của hệ: \(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Theo đề bài, ta có: \(\overrightarrow {{p_1}} \bot \overrightarrow {{p_2}} \)
Ta suy ra \(p = \sqrt {p_1^2 + p_2^2} \)
Lại có: \(\left\{ \begin{array}{l}{p_1} = {m_1}{v_1} = 0,4.6 = 2,4kg.m/s\\{p_2} = {m_2}{v_2} = 0,2.12 = 2,4kg.m/s\end{array} \right.\)
Suy ra \(p = \sqrt {2,{4^2} + 2,{4^2}} = 2,4\sqrt 2 \approx 3,39kg.m/s\)
Một vật có khối lượng 2 kg rơi tự do xuống đất trong khoảng thời gian 0,5s. Độ biến thiên động lượng của vật trong khoảng thời gian đó là bao nhiêu ? Cho g = 9,8 m/s2.
Vật được thả rơi nên: \({v_1} = 0\)
Tốc độ của vật sau 0,5s: \({v_2} = g.t = 9,8.0,5 = 4,9m/s\)
Động lượng của vật: \(\left\{ \begin{array}{l}{p_1} = 0\\{p_2} = m.{v_2} = 2.4,9 = 9,8\,kg.m/s\end{array} \right.\)
Độ biến thiên động lượng: \(\Delta p = {p_2} = 9,8kg.m/s\)
Hệ gồm hai vật có động lượng là \({p_1} = 2,4kg.m/s\) và \({p_2} = 2,4kg.m/s\). Động lượng tổng cộng của hệ \(p = 4,8kg.m/s\) nếu:
Ta có:
\(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Xét về mặt độ lớn, ta có:
\(p = 4,8kg.m/s = {p_1} + {p_2}\)
Ta suy ra \(\overrightarrow {{p_1}} \uparrow \uparrow \overrightarrow {{p_2}} \)
Một vật có khối lượng 1 kg được thả rơi tự do. Cho g = 10 m/s2. Sau 2s động lượng của vật là:
Tốc độ của vật sau 2s: \(v = g.t = 10.2 = 20m/s\)
Động lượng của vật sau 2s: \(p = m.v = 1.20 = 20\,kg.m/s\)
Phát biểu nào sau đây là đúng? Trong một hệ kín
A - đúng
B – sai vì: Trong hệ kín, động lượng của hệ được bảo toàn
C – sai vì: Trong hệ kín không có ngoại lực tác dụng hoặc các hợp các ngoại lực tác dụng lên vật bằng 0
D - sai