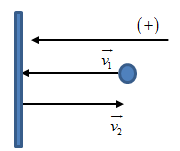
Một vật có khối lượng \(100g\) chuyển động với vận tốc \(2,5m/s\) đến va chạm với một vật có khối lượng \(150g\) đang đứng yên. Coi va chạm giữa hai vật là mềm. Sau va chạm, hai vật dính nhau và chuyển động với cùng vận tốc
Hệ hai vật ngay khi va chạm mềm là một hệ kín nên động lượng của hệ được bảo toàn (Động lượng của hệ trước và sau va chạm bằng nhau):
\(\begin{array}{l}\overrightarrow {{p_{trc}}} = \overrightarrow {{p_{sau}}} \\ \Leftrightarrow {m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} = \left( {{m_1} + {m_2}} \right)\overrightarrow v \end{array}\)
Có ban đầy vật 2 đứng yên \( \Rightarrow {v_2} = 0\)
Ta suy ra: \(v = \dfrac{{{m_1}{v_1}}}{{\left( {{m_1} + {m_2}} \right)}} = \dfrac{{0,1.2,5}}{{0,1 + 0,15}} = 1m/s\)
Một vật có khối lượng 2 kg rơi tự do xuống đất trong khoảng thời gian 0,5s. Độ biến thiên động lượng của vật trong khoảng thời gian đó là bao nhiêu ? Cho g = 9,8 m/s2.
Vật được thả rơi nên: \({v_1} = 0\)
Tốc độ của vật sau 0,5s: \({v_2} = g.t = 9,8.0,5 = 4,9m/s\)
Động lượng của vật: \(\left\{ \begin{array}{l}{p_1} = 0\\{p_2} = m.{v_2} = 2.4,9 = 9,8\,kg.m/s\end{array} \right.\)
Độ biến thiên động lượng: \(\Delta p = {p_2} = 9,8kg.m/s\)
Chiếc xe chạy trên đường ngang với vận tốc 10m/s va chạm mềm vào một chiếc xe khác đang đứng yên và có cùng khối lượng. Biết va chạm là va chạm mềm, sau va chạm vận tốc hai xe là:
Động lượng ban đầu của hệ: \(\overrightarrow {{p_1}} = m.\overrightarrow v \)
Động lượng của hệ sau khi va chạm: \(\overrightarrow {{p_2}} = \left( {{m_1} + {m_2}} \right)\overrightarrow {v'} = 2m.\overrightarrow {v'} \)
Áp dụng định luật bảo toàn động lượng cho lúc trước và sau va chạm ta có:
\(\begin{array}{l}\overrightarrow {{p_1}} = \overrightarrow {{p_2}} \Leftrightarrow m.\overrightarrow v = 2m.\overrightarrow {v'} \Leftrightarrow v = 2v' \Rightarrow v' = \dfrac{v}{2} = \dfrac{{10}}{2} = 5m/s\\ \Rightarrow {v_1} = {v_2} = 5m/s\end{array}\)
Một vật có khối lượng 1 kg được thả rơi tự do. Cho g = 10 m/s2. Sau 2s động lượng của vật là:
Tốc độ của vật sau 2s: \(v = g.t = 10.2 = 20m/s\)
Động lượng của vật sau 2s: \(p = m.v = 1.20 = 20\,kg.m/s\)
Hai vật có khối lượng m1 = m2 = 1kg, chuyển động với vận tốc tương ứng là v1 = 2 m/s, v2 = 1 m/s, biết chúng chuyển động ngược hướng. Động lượng của hệ có độ lớn là.
Chọn chiều dương là chiều chuyển động của vật 1.
Áp dụng công thức tính tổng động lượng
\(\overrightarrow p = {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} \Rightarrow p = 1.2 - 1.1 = 1\left( {kg.m/s} \right)\)
Một quả bóng có khối lượng 0,2kg chuyển động với vận tốc 2m/s đến đập vuông góc vào một bức tường và bật ngược trở lại với vận tốc có phương và độ lớn như cũ, chọn chiều dương là chiều của vận tốc khi bật ra khỏi tường. Độ biến thiên động lượng của quả bóng là
Chọn chiều dương là chiều của vận tốc khi bật ra khỏi tường, vậy ta có :
\(\begin{array}{l}
\overrightarrow {\Delta p} = \overrightarrow {{p_2}} - \overrightarrow {{p_1}} = m.\overrightarrow v - m.( - \overrightarrow v ) = 2m\overrightarrow v \\
\Rightarrow \Delta p = 2mv = 2.0,2.2 = 0,8kg.m/s
\end{array}\)
Chiếc xe chạy trên đường ngang với vận tốc 20m/s va chạm với một chiếc xe khác đang đứng yên và có cùng khối lượng. Biết va chạm là va chạm mềm, sau va chạm vận tốc hai xe là :
Xét hệ cô lập gồm hai xe.
Gọi m là khối lượng mỗi xe.
Động lượng lúc trước va chạm của hệ :
\(\overrightarrow{{{p}_{tr}}}=m.\overrightarrow{{{v}_{1}}}+m.\overrightarrow{{{v}_{2}}}=m.\overrightarrow{{{v}_{1}}}\)
Động lượng của hệ sau va chạm :
\(\overrightarrow{{{p}_{s}}}=\left( {{m}_{1}}+{{m}_{2}} \right)\overrightarrow{v}=2m.\overrightarrow{v}\)
Động lượng được bảo toàn :
\(\begin{gathered}
\overrightarrow {{p_{tr}}} = \overrightarrow {{p_s}} \Leftrightarrow m.\overrightarrow {{v_1}} = 2m.\overrightarrow v \Leftrightarrow \overrightarrow {{v_1}} = 2.\overrightarrow v \hfill \\
\Rightarrow v = \frac{{{v_1}}}{2} = \frac{{20}}{2} = 5 = 10m/s \hfill \\
\Rightarrow {v_1}' = {v_2}' = 10m/s \hfill \\
\end{gathered} \)
Một quả bóng khối lượng m đang bay ngang với vận tốc v thì đập vào bức tường và bật trở lại với cùng một vận tốc. Chọn chiều dương là chiều chuyển động của quả bóng ban đầu đến đập vào tường. Độ biến thiên động lượng của quả bóng là:
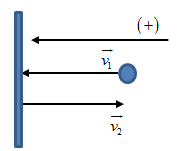
Động lượng trước va chạm của bóng: \(\overrightarrow{{{p}_{1}}}=m.\overrightarrow{{{v}_{1}}}\), độ lớn: \({{p}_{1}}=m.{{v}_{1}}=mv\)
Động lượng sau va chạm: \(\overrightarrow{{{p}_{2}}}=m.\overrightarrow{{{v}_{2}}}\), độ lớn : \({{p}_{2}}=m.{{v}_{2}}=m.v\)
Độ biến thiên động lượng : \(\overrightarrow{\Delta p}=\overrightarrow{{{p}_{2}}}-\overrightarrow{{{p}_{1}}}=m.\overrightarrow{{{v}_{2}}}-m.\overrightarrow{{{v}_{1}}}\,\,\,\left( * \right)\)
Chiếu (*) lên chiều dương ta có: \(\Delta p=-m.{{v}_{2}}-m.{{v}_{1}}=-mv-mv=-2mv\)
Người ta ném một quả bóng khối lượng 10kg cho nó chuyển động với vận tốc 20m/s. Xung lượng của lực tác dụng lên quả bóng là:
Độ biến thiên động lượng: \(\overrightarrow{\Delta p}=\overrightarrow{F}.\Delta t\)
Về độ lớn: \(\Delta p=F.\Delta t\)
Độ biến thiên động lượng: \(\overrightarrow{\Delta p}=\overrightarrow{{{p}_{2}}}-\overrightarrow{{{p}_{1}}}=m.\overrightarrow{{{v}_{2}}}-m.\overrightarrow{{{v}_{1}}}\,\,\,\left( \overrightarrow{{{v}_{1}}}=0 \right)\)
\(\Rightarrow \overrightarrow{\Delta p}=m.\overrightarrow{{{v}_{2}}}\Rightarrow \Delta p=m.{{v}_{2}}=10.20=200\,\,\left( kg.m/s \right)\)
Vì \(\Delta p=F.\Delta t\) nên xung lượng của lực bằng 10 (N.s)
Một khẩu súng đại bác nằm ngang khối lượng ms = 1000kg, bắn một viên đạn khối lượng mđ = 2,5kg. Vận tốc viên đạn ra khỏi nòng súng là 600m/s. Tìm vận tốc của súng sau khi bắn:
Ban đầu khẩu súng đại bác nằm yên nên động lượng của súng khi chưa bắn: \(\overrightarrow {{p_1}} = 0\)
Động lượng của hệ sau khi bắn súng là: \(\overrightarrow {{p_2}} = {m_s}.\overrightarrow {{v_s}} + {m_d}.\overrightarrow {{v_d}} \)
Áp dụng định luật bảo toàn động lượng ta có: \({m_s}.\overrightarrow {{v_s}} + {m_d}.\overrightarrow {{v_d}} = 0\)
Chọn chiều dương là chiều chuyển động của đạn bay ra khỏi nòng súng. Ta có:
\({m_s}.{v_s} + {m_d}.{v_d} = 0 \Rightarrow {v_s} = - \dfrac{{{m_d}.{v_d}}}{{{m_s}}} = - \dfrac{{600.2,5}}{{1000}} = - 1,5m/s\)
Vậy sau khi bắn súng bị giật ngược lại với vận tốc 1,5m/s
Hai vật có khối lượng m1 = 1kg, m2 = 3kg chuyển động với các vận tốc v1 = 3m/s và v2 = 1m/s. Tìm tổng động lượng của hệ khi \(\overrightarrow {{v_1}} \) và \(\overrightarrow {{v_2}} \) vuông góc với nhau:
Ta có độ lớn động lượng của vật 1 và vật hai là \(\left\{ \begin{array}{l}{p_1} = {m_1}.{v_1} = 1.3 = 3\,\,kg.m/s\\{p_2} = {m_2}.{v_2} = 3.1 = 3\,\,kg.m/s\end{array} \right.\)
Động lượng của hệ: \(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Do \(\overrightarrow {{v_1}} \bot \overrightarrow {{v_2}} \Rightarrow p = \sqrt {p_1^2 + p_2^2} = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \,\,kg.m/s\)
Xe A có khối lượng 1000 kg và vận tốc 60 km/h; xe B có khối lượng 2000 kg và vận tốc 30 km/h . So sánh động lượng của chúng.
Ta có: \(\left\{ \begin{array}{l}{m_A} = 1000kg\\{v_A} = 60km/h = \dfrac{{50}}{3}m/s\\{m_B} = 2000kg\\{v_B} = 30km/h = \dfrac{{25}}{3}m/s\end{array} \right.\)
Ta có: \(p = mv \Rightarrow \left\{ \begin{array}{l}{p_A} = {m_A}.{v_A} = 1000.\dfrac{{50}}{3} = \dfrac{{50000}}{3}\,\,kg.m/s\\{p_B} = {m_B}.{v_B} = 2000.\dfrac{{25}}{3} = \dfrac{{50000}}{3}\,\,kg.m/s\end{array} \right. \Rightarrow {p_A} = {p_B}\)
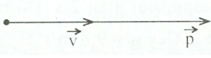
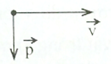
Hình nào biểu diễn đúng quan hệ giữa \(\overrightarrow v \) và \(\overrightarrow p \) của một chất điểm?
Ta có: \(\overrightarrow p = m\overrightarrow v \)
\( \to \overrightarrow p \uparrow \uparrow \overrightarrow v \)
Phát biểu nào sau đây không đúng?
A, B, D - đúng
C - sai vì: Đơn vị của động lượng là \(kg.m/s\) hoặc \(N.s\) còn đơn vị của năng lượng là J
Một vật khối lượng \(500{\rm{ }}g\) chuyển động thẳng dọc trục Ox với vận tốc \(18{\rm{ }}km/h\). Động lượng của vật bằng:
Ta có: \(18km/h = 5m/s\)
Động lượng của vật: \(\overrightarrow p = m\overrightarrow v \)
Xét về độ lớn: \(p = mv = 0,5.5 = 2,5kg.m/s\)
Trong quá trình nào sau đây, động lượng của vật không thay đổi?
Động lượng của vật: \(\overrightarrow p = m\overrightarrow v \)
Động lượng của một vật không đổi nếu \(\overrightarrow v \) không đổi.
Chất điểm M chuyển động không vận tốc đầu dưới tác dụng của lực không đổi \(\overrightarrow F \).Động lượng chất điểm ở thời điểm t là:
Ta có: Độ biến thiên động lượng của một vật trong một khoảng thời gian nào đó bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó.
\(\overrightarrow {{p_2}} - \overrightarrow {{p_1}} = \Delta \overrightarrow p = \overrightarrow F \Delta t\)
Ta có: Do vật chuyển động không vận tốc đầu nên:
\(\begin{array}{l}\Delta \overrightarrow p = \overrightarrow {{p_2}} = \overrightarrow p = \overrightarrow F t\\ \to \overrightarrow p = \overrightarrow F t\end{array}\)
Một chất điểm chuyển động không vận tốc đầu dưới tác dụng của lực không đổi \(F = 0,1{\rm{ }}N\). Động lượng chất điểm ở thời điểm \(t = 3{\rm{ }}s\) kể từ lúc bắt đầu chuyển động là:
Ta có: Độ biến thiên động lượng của một vật trong một khoảng thời gian nào đó bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó.
\(\overrightarrow {{p_2}} - \overrightarrow {{p_1}} = \Delta \overrightarrow p = \overrightarrow F \Delta t\)
Ta có: Do vật chuyển động không vận tốc đầu nên:
\(\Delta \overrightarrow p = \overrightarrow {{p_2}} = \overrightarrow F t\)
Xét về độ lớn, ta có: \({p_2} = F.t = 0,1.3 = 0,3N.s = 0,3kg.m/s\)
Trên hình là đồ thị tọa độ – thời gian của một vật có khối lượng \(3 kg\). Động lượng của vật tại thời điểm \(t_1= 1s\) và thời điểm \(t_2= 5 s\) lần lượt bằng:
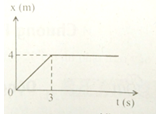
Thời điểm t = 0 đến thời điểm t = 3 s, vật chuyển động thẳng đều với vận tốc bằng 4/3 m/s.
Từ thời điểm t = 3 s vật không chuyển động.
=> Tại thời điểm t1 = 1 s ⇒ p1 = mv1 = 4 kg.m/s.
=> Tại thời điểm t2 = 5 s ⇒ p2 = mv2 = 0 kg.m/s.
Một vật \(3 kg\) rơi tự do rơi xuống đất trong khoảng thời gian \(2 s\). Độ biến thiên động lượng của vật trong khoảng thời gian đó là (lấy \(g = 9,8 m/s^2\)).
Xung lượng của trọng lực bằng độ biến thiên động lượng của vật:
\( \Rightarrow \Delta p = F.\Delta t\)
Ta có: \(F\) - ở đây chính là trọng lượng của vật \(P = mg\)
\( \Rightarrow \Delta p = P.\Delta t = mg.\Delta t = 3.9,8.2 = 58,8kg.m/s\)