Tính nhiệt độ ban đầu của một khối khí xác định biết rằng khi nhiệt độ tăng thêm 200C thì thể tích khí giảm đi 20% so với thể tích ban đầu, áp suất thì tăng thêm 30% so với áp suất ban đầu:
Xét lượng khí xác định trong phòng thí nghiệm:
\(TT1:\left\{ \begin{array}{l}{p_1}\\{V_1}\\{T_1}\end{array} \right. \to TT2:\left\{ \begin{array}{l}{p_2} = {p_1} + 0,3{p_1} = 1,3{p_1}\\{V_2} = {V_1} - 0,2{V_1} = 0,8{V_1}\\{T_2} = {T_1} + 20\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lí tưởng ta có:
\(\begin{array}{l}\dfrac{{{p_1}.{V_1}}}{{{T_1}}} = \dfrac{{{p_2}.{V_2}}}{{{T_2}}} \Leftrightarrow \dfrac{{{p_1}.{V_1}}}{{{T_1}}} = \dfrac{{1,3{p_1}.0,8{V_1}}}{{{T_1} + 20}}\\ \Leftrightarrow \dfrac{1}{{{T_1}}} = \dfrac{{1,04}}{{{T_1} + 20}} \Rightarrow {T_1} + 20 = 1,04{T_1} \Rightarrow {T_1} = 500K\end{array}\)
Thông số trạng thái của khí lí tưởng gồm:
Thông số trạng thái của một lượng khí gồm:
+ Thể tích
+ Nhiệt độ
+ Áp suất
Quá trình nào sau đây là đẳng quá trình:
Đun nóng khí trong một bình đậy kín là quá trình đẳng tích
Một xy-lanh chứa khí lí tưởng ở áp suất \(0,7atm\) và nhiệt độ \({47^0}C\). Tính nhiệt độ trong xy-lanh khi áp suất trong xy-lanh tăng thêm đến \(8atm\) còn thể tích trong xy-lanh giảm 5 lần?
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 47 + 273 = 320K\\{p_1} = 0,7{\rm{a}}tm\\{V_1} = V\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = ?\\{p_2} = 8atm\\{V_2} = \dfrac{V}{5}\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lý tưởng, ta có:
\(\begin{array}{l}\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}}\\ \Leftrightarrow \dfrac{{0,7.V}}{{320}} = \dfrac{{8.V}}{{5.{T_2}}}\\ \Rightarrow {T_2} = 731,4K\\ \Rightarrow {t_2} = {458,4^0}C\end{array}\)
Thể tích của hỗn hợp khí trong xi-lanh là \(2d{m^3}\), nhiệt độ là \({47^0}C\) và áp suất ban đầu là \(1atm\). Tính nhiệt độ của hỗn hợp khí trong xi-lanh khi pit-tông nén khí trong xi-lanh làm thể tích giảm đi 10 lần, áp suất tăng đến \(15atm\).
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{p_1} = 1{\rm{a}}tm\\{V_1} = 2l\\{T_1} = 273 + 47 = 320K\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{p_2} = 15atm\\{V_2} = 0,2l\\{T_2} = ?\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lý tưởng, ta có:
\(\begin{array}{l}\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}} \leftrightarrow \dfrac{{1.2}}{{320}} = \dfrac{{15.0,2}}{{{T_2}}}\\ \to {T_2} = 480K\end{array}\)
Bình kín được ngăn làm hai phần bằng nhau (phần A, phần B) bằng tấm cách nhiệt có thể dịch chuyển được. Biết mỗi bên có chiều dài \(30cm\) và nhiệt độ của khí trong bình là \({27^0}C\). Xác định khoảng dịch chuyển của tấm cách nhiệt khi nung nóng phần A thêm \({10^0}C\) và làm lạnh phần B đi \({10^0}C\)
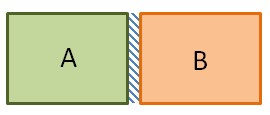
Gọi \(h\) là chiều cao của bình, \(y\) chiều rộng của bình, \(x\) là khoảng vách ngăn dịch chuyển.
Ta có:
+ Phần A:
- Trạng thái 1: \(\left\{ \begin{array}{l}{V_0} = h.{l_0}y\\{p_0}\\{T_0} = 27 + 273 = 300K\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{V_A} = h\left( {{l_0} + x} \right)\\{p_A}\\{T_A} = 310K\end{array} \right.\)
+ Phần B:
- Trạng thái 1: \(\left\{ \begin{array}{l}{V_0} = h{l_0}y\\{p_0}\\{T_0} = 27 + 273 = 300K\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{V_B} = h\left( {{l_0} - x} \right)y\\{p_B}\\{T_B} = 290K\end{array} \right.\)
Để vách ngăn nằm cân bằng sau khi nung nóng một bên và làm lạnh một bên thì áp suất của phần A và phần B sau khi nung nóng phải bằng nhau: \({p_A} = {p_B}\)
+ Áp dụng phương trình trạng thái của khí lí tưởng cho mỗi phần ta được:
\(\dfrac{{{p_0}{V_0}}}{{{T_0}}} = \dfrac{{{p_A}{V_A}}}{{{T_A}}}\) (1)
\(\dfrac{{{p_0}{V_0}}}{{{T_0}}} = \dfrac{{{p_B}{V_B}}}{{{T_B}}}\) (2)
Lấy \(\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(1 = \dfrac{{\dfrac{{{p_A}{V_A}}}{{{T_A}}}}}{{\dfrac{{{p_B}{V_B}}}{{{T_B}}}}} \Leftrightarrow \dfrac{{{V_A}}}{{{V_B}}} = \dfrac{{{T_A}}}{{{T_B}}}\) (do \({p_A} = {p_B}\))
\(\begin{array}{l} \Leftrightarrow \dfrac{{h\left( {{l_0} + x} \right)y}}{{h\left( {{l_0} - x} \right)y}} = \dfrac{{310}}{{290}}\\ \Leftrightarrow \dfrac{{{l_0} + x}}{{{l_0} - x}} = \dfrac{{31}}{{29}} \Leftrightarrow \dfrac{{30 + x}}{{30 - x}} = \dfrac{{31}}{{29}}\\ \Rightarrow x = 1cm\end{array}\)
Một máy nén khí ở áp suất \(1atm\) mỗi lần nén được \(4\) lít khí ở nhiệt độ \({27^0}C\) vào trong bình chứa thể tích \(2{m^3}\) áp suất ban đầu \(1atm\). Tính áp suất bên trong bình chứa sau \(1000\) lần nén khí. Biết nhiệt độ trong bình sau \(1000\) lần nén là \({42^0}C\)
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 27 + 273 = 300K\\{p_1} = 1{\rm{a}}tm\\{V_1} = nV = 1000.4 = 4000l\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = 42 + 273 = 315K\\{p_2} = ?\\{V_2} = 2{m^3} = 2000l\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lý tưởng, ta có:
\(\begin{array}{l}\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}}\\ \Rightarrow {p_2} = \dfrac{{{p_1}{V_1}{T_2}}}{{{T_1}{V_2}}} = \dfrac{{1.4000.315}}{{300.2000}} = 2,1atm\end{array}\)
Khí cầu có dung tích \(328{m^3}\) được bơm khí Hiđro. Khi bơm xong, hiđro trong khí cầu có nhiệt độ \({27^0}C\), áp suất \(0,9atm\). Hỏi phải bơm bao nhiêu lâu nếu mỗi giây bơm được \(2,5g\) hiđro vào khí cầu.
Ta có:
- Thể tích: \(V = 328{m^3} = {328.10^3}l\)
- Nhiệt độ: \(T = 27 + 273 = 300K\)
- Áp suất: \(p = 0,0{\rm{a}}tm\)
Gọi m là khối khí đã bơm vào khí cầu, áp dụng phương trình Cla-pe-rôn - Men-đê-lê-ép, ta có:
\(pV = \dfrac{m}{M}RT \to m = M\dfrac{{pV}}{{RT}} = 2.\dfrac{{0,{{9.328.10}^3}}}{{0,082.300}} = 24000g\)
Biết mỗi giây bơm được \(2,5g\) hiđrô vào khí cầu
=> Thời gian để bơm được \(m\left( g \right)\) hiđrô vào khí cầu là:
\(t = \dfrac{m}{{2,5}} = \dfrac{{24000}}{{2,5}} = 9600{\rm{s}} = 160phut= \dfrac{8}{3}h\)
Một chất khí có khối lượng \(1g\) ở nhiệt độ \({27^0}C\) dưới áp suất \(0,5atm\) và có thể tích là \(1,8\) lít. Hỏi khí đó là khí gì? Biết rằng đó là một đơn chất.
- Khi khí trong bình là Hiđrô: \(\left\{ \begin{array}{l}{m_1} = 1g\\{T_1} = 27 + 273 = 300K\\{p_1} = 0,5atm\\V = 1,8l\end{array} \right.\)
Sử dụng phương trình Cla-pe-rôn - Men-đê-lê-ép ta có:
\(V = \dfrac{m}{M}\dfrac{{RT}}{p} \to {\rm{M = 28 }}\)
=> Chất khí được đó là \({N_2}\) có \(M = 28\)
Một bình kín chứa 1 mol khí Nito, áp suất \({10^5}Pa\), ở nhiệt độ \({27^0}C\). Do có một lượng khí thoát ra ngoài nên áp suất của khí trong bình chỉ còn \(0,{8.10^5}Pa\), nhiệt độ vẫn được giữ không đổi. Lượng khí đã thoát ra ngoài bằng:
Ta có:
- Ban đầu, khí Nito có khối lượng \(m\), thể tích \(V\), áp suất \(p\), nhiệt độ \(T\)
PT: \({p_1}V = \dfrac{m}{M}RT{\rm{ }}\left( 1 \right)\)
- Sau một thời gian, khí Heli có khối lượng \(m'\), thể tích \(V\), áp suất \({p_2}\), nhiệt độ \(T\)
PT: \({p_2}V = \dfrac{{m'}}{M}RT{\rm{ }}\left( 2 \right)\)
Lấy \(\dfrac{{\left( 2 \right)}}{{\left( 1 \right)}}\) ta được:
\(\dfrac{{{p_2}}}{{{p_1}}} = \dfrac{{m'}}{m} \leftrightarrow \dfrac{{0,8}}{1} = \dfrac{{m'}}{m} \to m' = 0,8m\)
=> Lượng khí Nito đã thoát ra:
\(\Delta m = m - m' = m - 0,8m = 0,2m = 0,2.1.28 = 5,6g\)
Số mol khí Nito thoát ra ngoài là: \(n=\dfrac{m}{M}=\dfrac{5,6}{28}=0,2mol\)
Vậy lượng khí đã thoát ra ngoài bằng: 0,2mol
Hai xilanh chứa 2 loại khí có khối lượng mol là \({M_1},{M_2}\) khác nhau nhưng có cùng khối lượng \(m\). Áp suất của hai khí cũng bằng nhau. Quá trình biến đổi đẳng áp được biểu diễn bởi các đồ thị như hình dưới.
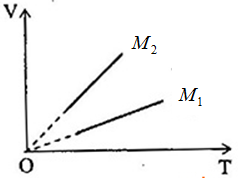
Nhận xét nào dưới đây là đúng.

Vẽ đường thẳng qua \({T_1}\) , song song với trục OV, cắt đồ thị (V,T) của hai khí tại \(A\left( {{p_1},{V_1},{T_2}} \right)\) và \(B\left( {{p_1},{V_2},{T_1}} \right)\)
Viết phương trình Cla-pe-rôn - Men-đê-lê-ép cho hai trạng thái, ta được:
\(\left\{ \begin{array}{l}{p_1}{V_1} = \dfrac{m}{{{M_1}}}R{T_1}{\rm{ }}\left( 1 \right)\\{p_1}{V_2} = \dfrac{m}{{{M_2}}}R{T_1}{\rm{ }}\left( 2 \right)\end{array} \right.\)
Từ (1) và (2) suy ra: \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{M_2}}}{{{M_1}}}\)
Mặt khác, từ đồ thị, ta thấy: \({V_1} < {V_2}\) ta suy ra \({M_2} < {M_1}\)
Tính nhiệt độ ban đầu của một khối khí xác định biết rằng khi nhiệt độ tăng thêm 160C thì thể tích khí giảm đi 10% so với thể tích ban đầu, áp suất thì tăng thêm 20% so với áp suất ban đầu:
Xét lượng khí xác định trong phòng thí nghiệm:
\(TT1:\left\{ \begin{array}{l}{p_1}\\{V_1}\\{T_1}\end{array} \right. \to TT2:\left\{ \begin{array}{l}{p_2} = {p_1} + 0,2{p_1} = 1,2{p_1}\\{V_2} = {V_1} - 0,1{V_1} = 0,9{V_1}\\{T_2} = {T_1} + 16\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lí tưởng ta có:
\(\begin{array}{l}\dfrac{{{p_1}.{V_1}}}{{{T_1}}} = \dfrac{{{p_2}.{V_2}}}{{{T_2}}} \Leftrightarrow \dfrac{{{p_1}.{V_1}}}{{{T_1}}} = \dfrac{{1,2{p_1}.0,9{V_1}}}{{{T_1} + 16}}\\ \Leftrightarrow \dfrac{1}{{{T_1}}} = \dfrac{{1,08}}{{{T_1} + 16}} \Rightarrow {T_1} = 200K\end{array}\)
Một khối khí lí tưởng thực hiện quá trình được biểu diễn như hình.
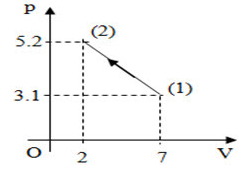
Các số liệu như trên đồ thị. Biết ở trạng thái ban dầu, nhiệt độ của khối khí là \({37^0}C\). Nhiệt độ của khối khí ở cuối quá trình là:
Xét các trạng thái của khí:
+ Trạng thái 1: \(\left\{ \begin{array}{l}{p_1} = 3,1\\{V_1} = 7\\{T_1} = 37 + 273 = 310K\end{array} \right.\)
+ Trạng thái 2: \(\left\{ \begin{array}{l}{p_2} = 5,2\\{V_2} = 2\\{T_2} = ?\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lí tưởng, ta có: \(\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow {T_2} = \dfrac{{{p_2}{V_2}}}{{{p_1}{V_1}}}{T_1} = \dfrac{{5,2.2}}{{3,1.7}}.310 = 148,6K\)
Một lượng khí biến đổi theo chu trình biểu diễn bởi đồ thị.
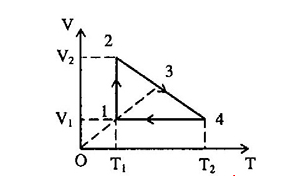
Cho biết \({p_1} = {p_3}\), \({V_1} = 1{m^3}\), \({V_2} = 4{m^3}\), \({T_1} = 100K\), \({T_4} = 300K\). Tìm giá trị của \({V_3}\)?
Ta có:
- Quá trình \(\left( 1 \right) \to \left( 2 \right)\): Quá trình đẳng nhiệt: \({T_2} = {T_1} = 100K\) , \({V_2} = 4{m^3}\)
- Quá trình \(\left( 4 \right) \to \left( 1 \right)\): Quá trình đẳng tích: \({V_4} = {V_1} = 1{m^3}\), \({T_4} = 300K\)
- Qúa trình \(\left( 2 \right) \to \left( 4 \right)\): \(V = aT + b\)
+ Trạng thái 2: \(4 = 100a + b\) (1)
+ Trạng thái 4: \(1 = 300a + b\) (2)
Từ \(\left( 1 \right),\left( 2 \right)\) ta suy ra: \(\left\{ \begin{array}{l}a = - \dfrac{3}{{200}}\\b = \dfrac{{11}}{2}\end{array} \right.\)
\( \Rightarrow V = - \dfrac{3}{{200}}T + \dfrac{{11}}{2}\) (3)
- Quá trình \(\left( 1 \right) \to \left( 3 \right)\): Quá trình đẳng áp \(V = \dfrac{{{V_1}}}{{{T_1}}}T = \dfrac{1}{{100}}T\) (4)
Vì \(\left( 3 \right)\) là giao điểm của 2 đường \(\left( 2 \right) \to \left( 4 \right)\) và \(\left( 1 \right) \to \left( 3 \right)\) nên:
\(\begin{array}{l} - \dfrac{3}{{200}}{T_3} + \dfrac{{11}}{2} = \dfrac{1}{{100}}{T_3}\\ \Rightarrow {T_3} = 220K\end{array}\)
Thay vào (4) suy ra \({V_3} = \dfrac{{220}}{{100}} = 2,2{m^3}\)
Một phòng có kích thước \(8m \times 5m \times 4m\). Ban đầu không khí trong phòng ở điều kiện chuẩn, sau đó nhiệt độ của không khí tăng lên tới 120C, trong khi áp suất là 79cmHg. Thể tích của lượng không khí đã ra khỏi phòng xấp xỉ bằng:
Xét lượng khí xác định trong phòng thí nghiệm:
\(TT1:\left\{ \begin{array}{l}{p_1} = 76cmHg\\{V_1} = 5.8.4 = 160{m^3}\\{T_1} = 0 + 273 = 273K\end{array} \right. \to TT2:\left\{ \begin{array}{l}{p_2} = 79cmHg\\{V_2} = ?\\{T_2} = 12 + 273 = 285K\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lí tưởng ta có:
\(\dfrac{{{p_1}.{V_1}}}{{{T_1}}} = \dfrac{{{p_2}.{V_2}}}{{{T_2}}} \Rightarrow {V_2} = \dfrac{{{p_1}.{V_1}.{T_2}}}{{{p_2}.{T_1}}} = \dfrac{{76.160.285}}{{79.273}} = 160,7{m^3}\)
Thể tích không khí thoát ra khỏi phòng:
\(\Delta V = {V_2} - {V_1} = 160,7 - 160 = 0,7{m^3}\)
Trong phòng thí nghiệm, người ta điều chế được 60cm3 khí hidro ở áp suất 750 mmHg và nhiệt độ 370C Tính thể tích của lượng khí trên ở điều kiện chuẩn (áp suất 760 mmHg và nhiệt độ 00C)?
Xét lượng khí xác định trong phòng thí nghiệm:
\(TT1:\left\{ \begin{array}{l}{p_1} = 750mmHg\\{V_1} = 60c{m^3}\\{T_1} = 37 + 273 = 310K\end{array} \right. \to TT2\,\left( {dktc} \right):\left\{ \begin{array}{l}{p_2} = 760mmHg\\{V_2} = ?\\{T_2} = 0 + 273 = 273K\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lí tưởng ta có:
\(\dfrac{{{p_1}.{V_1}}}{{{T_1}}} = \dfrac{{{p_2}.{V_2}}}{{{T_2}}} \Rightarrow {V_2} = \dfrac{{{p_1}.{V_1}.{T_2}}}{{{p_2}.{T_1}}} = \dfrac{{750.60.273}}{{760.310}} = 52,14c{m^3}\)
Đại lượng không phải thông số trạng thái của một lượng khí là
Thông số trạng thái của một lượng khí gồm:
+ Thể tích
+ Nhiệt độ
+ Áp suất
Tập hợp ba thông số xác định trạng thái của một lượng khí xác định là
Thông số trạng thái của một lượng khí gồm:
+ Thể tích
+ Nhiệt độ
+ Áp suất
Quá trình nào sau đây là đẳng quá trình.
Đun nóng khí trong một bình đậy kín là quá trình đẳng tích
Biểu thức nào dưới đây diễn tả phương trình trạng thái khí lý tưởng?
Phương trình trạng thái của khí lý tưởng: \(\frac{{pV}}{T} = const\)

