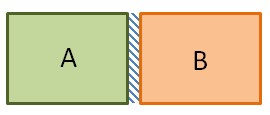
Bình kín được ngăn làm hai phần bằng nhau (phần A, phần B) bằng tấm cách nhiệt có thể dịch chuyển được. Biết mỗi bên có chiều dài $30cm$ và nhiệt độ của khí trong bình là ${27^0}C$. Xác định khoảng dịch chuyển của tấm cách nhiệt khi nung nóng phần A thêm ${10^0}C$ và làm lạnh phần B đi ${10^0}C$

Gọi $h$ là chiều cao của bình, $y$ chiều rộng của bình, $x$ là khoảng vách ngăn dịch chuyển.

Ta có:

+ Phần A:

- Trạng thái 1: $\left\{ \begin{array}{l}{V_0} = h.{l_0}y\\{p_0}\\{T_0} = 27 + 273 = 300K\end{array} \right.$

- Trạng thái 2: $\left\{ \begin{array}{l}{V_A} = h\left( {{l_0} + x} \right)\\{p_A}\\{T_A} = 310K\end{array} \right.$

+ Phần B:

- Trạng thái 1: $\left\{ \begin{array}{l}{V_0} = h{l_0}y\\{p_0}\\{T_0} = 27 + 273 = 300K\end{array} \right.$

- Trạng thái 2: $\left\{ \begin{array}{l}{V_B} = h\left( {{l_0} - x} \right)y\\{p_B}\\{T_B} = 290K\end{array} \right.$

Để vách ngăn nằm cân bằng sau khi nung nóng một bên và làm lạnh một bên thì áp suất của phần A và phần B sau khi nung nóng phải bằng nhau: ${p_A} = {p_B}$

+ Áp dụng phương trình trạng thái của khí lí tưởng cho mỗi phần ta được:

$\dfrac{{{p_0}{V_0}}}{{{T_0}}} = \dfrac{{{p_A}{V_A}}}{{{T_A}}}$   (1)

$\dfrac{{{p_0}{V_0}}}{{{T_0}}} = \dfrac{{{p_B}{V_B}}}{{{T_B}}}$ (2)

Lấy $\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}}$ ta được: $1 = \dfrac{{\dfrac{{{p_A}{V_A}}}{{{T_A}}}}}{{\dfrac{{{p_B}{V_B}}}{{{T_B}}}}} \Leftrightarrow \dfrac{{{V_A}}}{{{V_B}}} = \dfrac{{{T_A}}}{{{T_B}}}$  (do ${p_A} = {p_B}$)

$\begin{array}{l} \Leftrightarrow \dfrac{{h\left( {{l_0} + x} \right)y}}{{h\left( {{l_0} - x} \right)y}} = \dfrac{{310}}{{290}}\\ \Leftrightarrow \dfrac{{{l_0} + x}}{{{l_0} - x}} = \dfrac{{31}}{{29}} \Leftrightarrow \dfrac{{30 + x}}{{30 - x}} = \dfrac{{31}}{{29}}\\ \Rightarrow x = 1cm\end{array}$