0,2 mol khí ở áp suất \({p_1}\; = 2,5atm\), nhiệt độ \({t_1}\; = {0^0}C\) có thể tích \({V_1}\; = 1,15l\). Làm cho khí nóng lên đến nhiệt độ \({t_2}\; = {105^0}C\) và giữ nguyên thể tích khối khí. Tính áp suất p2 của khí?
Áp dụng định luật Sác – lơ ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \dfrac{{{p_1}{T_2}}}{{{T_1}}} = \dfrac{{2,5.378}}{{273}} = 3,46atm\)
Một bình được nạp khí ở nhiệt độ 350C dưới áp suất 350kPa. Sau đó bình được chuyển đến một nơi có nhiệt độ 400C, tính độ tăng áp suất của khí trong bình.
Áp dụng định luật Sác – lơ ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \dfrac{{{p_1}{T_2}}}{{{T_1}}} = \dfrac{{350.313}}{{308}} \approx 356kPa\)
Độ tăng áp suất của khí trong bình là:\(\Delta p = 356 - 350 = 6kPa\)
Một săm xe máy được bơm căng không khí ở nhiệt độ 200C và áp suất 2,2atm. Hỏi áp suất của không khí trong săm là bao nhiêu và săm có bị nổ không, khi để ngoài nắng nhiệt độ 440C? Coi sự tăng thể tích của săm là không đáng kể và biết săm chỉ chịu được áp suất tối đa là 2,5 atm.
Áp dụng định luật Sác – lơ ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \dfrac{{{p_1}{T_2}}}{{{T_1}}} = \dfrac{{2,2.317}}{{293}} = 2,38atm < 2,5atm\)
Vậy săm không bị nổ.
Một chiếc lốp ôtô chứa không khí có áp suất 4bar và nhiệt độ 240C. Khi xe chạy nhanh, lốp xe nóng lên làm cho nhiệt độ không khí trong lốp xe tăng lên tới 550C. Tính áp suất của không khí trong lốp xe lúc này?
Cách đổi đơn vị: \({1bar = {{10}^5}Pa = 1atm}\)
Xét lượng khí chứa trong lốp xe.
\(TT1:\left\{ \begin{gathered}
{p_1} = 4bar \hfill \\
{T_1} = 24 + 273 = 297K \hfill \\
{V_1} \hfill \\
\end{gathered} \right.\xrightarrow{{V = con\,st}}TT2:\left\{ \begin{gathered}
{p_2} = ? \hfill \\
{T_2} = 55 + 273 = 328K \hfill \\
{V_2} = {V_1} \hfill \\
\end{gathered} \right.\)
Áp dụng định luật Saclo cho quá trình đẳng tích:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \dfrac{{{p_1}}}{{{T_1}}}.{T_2} = \dfrac{{4.328}}{{297}} = 4,42bar = 4,{42.10^5}Pa\)
Quá trình biến đổi trạng thái khi thể tích không đổi là quá trình
Quá trình đẳng tích là quá trình biến đổi trạng thái khi thể tích không đổi.
Hệ thức nào sau đây là hệ thức của định luật Sác-lơ
Ta có: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.
=>\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}}\)
Quá trình nào sau đây không phải là quá trình đẳng tích:
Quá trình đẳng tích là quá trình biến đổi trạng thái khi thể tích không đổi.
Một khối khí lí tưởng thực hiện quá trình đẳng tích ở hai thể tích khác nhau được biểu diễn trên hình vẽ. Quan hệ giữa \({V_1}\) và \({V_2}\) là:
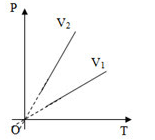
Vận dụng kiến thức về đường đẳng tích. Dựa vào đò thị ta có thể suy ra \({V_1} > {V_2}\)
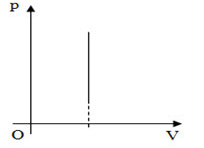
Trên đồ thị (p,V) đường đẳng tích là:
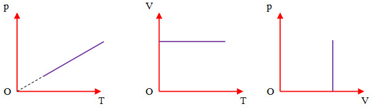
Trong hệ tọa độ (p,V) đường đẳng tích là đường thẳng song song với trục p.
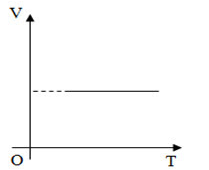
Trên đồ thị (V,T) đường đẳng tích là đường:
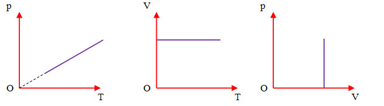
Trong hệ tọa độ (V,T) đường đẳng tích là đường thẳng vuông góc với trục V.
Đặc điểm nào sau đây không phải của quá trình đẳng tích của một khối khí lí tưởng:
A, B, D - đúng
C - sai vì: \(p \sim T\)
Biểu thức nào sau đây đúng cho quá trình đẳng tích của khối khí lí tưởng:
Ta có: \(p \sim T\)
Một bình kín có thể tích không đổi chứa khí lí tưởng ở áp suất \(1,{5.10^5}Pa\) và nhiệt độ \({20^0}C\). Tính áp suất trong bình khi nhiệt độ trong bình tăng lên tới \({40^0}C\).
Vì thể tích của bóng đèn không đổi nên ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \to {p_2} = \dfrac{{{T_2}}}{{{T_1}}}{p_1} = \dfrac{{40 + 273}}{{20 + 273}}.1,{5.10^5} = 1,{6.10^5}\) (pa)
Một bình thép chứa khí ở nhiệt độ \({27^0}C\) và áp suất \(40atm\). Nếu tăng áp suất thêm \(10atm\) thì nhiệt độ của khí trong binh là:
Vì thể tích của bóng đèn không đổi nên ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \to {T_2} = \dfrac{{{P_2}}}{{{P_1}}}{T_1} = \dfrac{{40 + 10}}{{40}}.(27 + 273) = 375 - 273 = {102^0}C\)
Một khối khí lý tưởng được đựng trong bình kín. Khi khối khí được làm lạnh đi \({20^0}C\) thì áp suất của nó thay đổi \(1,2\) lần. Nhiệt độ ban đầu của khối khí là:
Ta có:
- Trạng thái 1: \({p_1} = p,{T_1} = t + 273\)
- Trạng thái 2: \({p_2} = \dfrac{p}{{1,2}},{T_2} = t + 273 - 20\)
Do thể tích không đổi, theo định luật Sáclơ, ta có:
\(\begin{array}{l}\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \leftrightarrow \dfrac{p}{{t + 273}} = \dfrac{{\dfrac{p}{{1,2}}}}{{t + 273 - 20}}\\ \to t = 120K\end{array}\)
Một chiếc lốp ô-tô chứa không khí ở \({25^0}C\). Khi xe chạy nhanh, lốp xe nóng lên, áp suất khí trong lốp tăng lên tới \(1,084\) lần. Lúc này nhiệt độ trong lốp xe bằng:
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 25 + 273 = 298K\\{p_1} = p\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = (273 + t)K\\{p_2} = 1,084p\end{array} \right.\)
Áp dụng biểu thức định luật Sáclơ, ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \to {T_2} = {T_1}\dfrac{{{p_2}}}{{{p_1}}} = 298\dfrac{{1,084p}}{p} = {50^0}C\)
Một bóng đèn dây tóc chứa khí trơ ở \({27^0}C\) và áp suất \(0,6atm\). Khi đèn sáng, áp suất không khí trong đèn là \(1atm\) và không làm vỡ bóng đèn. Coi dung tích của bóng đèn không đổi, nhiệt độ của khí trong đèn khi cháy sáng là:
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 27 + 273 = 300K\\{p_1} = 0,6atm.\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = ?\\{p_2} = 1{\rm{a}}tm\end{array} \right.\)
Áp dụng biểu thức định luật Sáclơ, ta có:
\(\begin{array}{l}\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \leftrightarrow \dfrac{{0,6}}{{300}} = \dfrac{1}{{{T_2}}}\\ \to {T_2} = {227^0}C\end{array}\)
Một bình đầy không khí ở điều kiện tiêu chuẩn \(\left( {{0^0}C;1,{{013.10}^5}Pa} \right)\), được đậy bằng một vật có khối lượng \(2kg\). Tiết diện của miệng bình \(10c{m^2}\). Tìm nhiệt độ lớn nhất của không khí trong bình để không khí không đẩy được nắp bình lên và thoát ra ngoài. Biết áp suất khí quyển là \({p_0} = {10^5}Pa\).
Ta có:
Lượng không khí trong bình được đun nóng trong một quá trình đẳng tích.
Trạng thái 1: \(\left\{ \begin{array}{l}{t_1}\; = {\rm{ }}{{\rm{0}}^0}C \to {T_1}\; = 0 + 273 = 273K\\{p_1}\; = {\rm{ }}1{\rm{ }}atm\end{array} \right.\) .
Trạng thái 2: \(\left\{ \begin{array}{l}{t_1}\; = ?\\{p_2}\; = \dfrac{F}{s} + {p_0}\end{array} \right.\)
Trong quá trình đẳng tích:
\(\dfrac{{{p_2}}}{{{T_2}}} = \dfrac{{{p_1}}}{{{T_1}}} \to {T_2} = \dfrac{{{p_2}{T_1}}}{{{p_1}}} = 323,{4^0}K\)
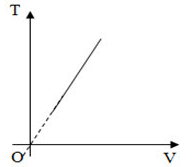
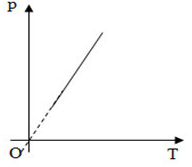
Đồ thị nào sau đây không biểu diễn quá trình đẳng tích:
đồ thị không biểu diễn đường đẳng tích là đồ thị ở hình a
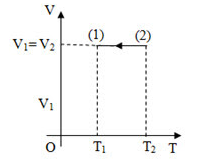
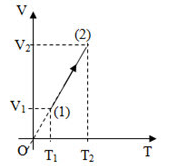
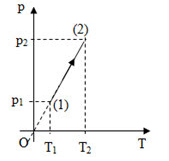
Một khối khí lí tưởng thực hiện quá trình được biểu diễn như trên hình vẽ. Đồ thị nào cũng biểu diễn đúng quá trình trên?
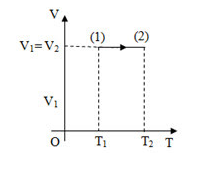
Qúa trình (1) -(2) là quá trình đẳng tích.
đồ thị biểu diễn đường đẳng tích là đồ thị ở hình B.