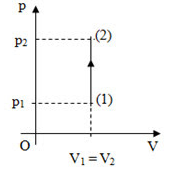
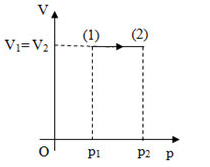
Một khối khí lí tưởng thực hiện quá trình như hình vẽ.
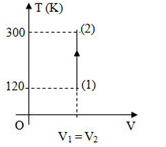
Các thông số được cho trên đồ thị, áp suất của khối khí khi kết thúc quá trình là \({4.10^5}Pa\). Áp suất của khối khí ở đầu quá trình là:
Ta có:
Lượng không khí trong bình được đun nóng trong một quá trình đẳng tích.
Trạng thái 1: \(\left\{ \begin{array}{l}{t_1}\; = {\rm{ 120}}K\\{p_1}\; = {\rm{ ?}}\end{array} \right.\) .
Trạng thái 2: \(\left\{ \begin{array}{l}{t_1}\; = 300K\\{p_2}\; = 4atm\end{array} \right.\)
Trong quá trình đẳng tích:
\(\dfrac{{{p_2}}}{{{T_2}}} = \dfrac{{{p_1}}}{{{T_1}}} \to {p_1} = \dfrac{{{p_2}{T_1}}}{{{T_1}}} = 1,58atm\)
Quá trình đẳng tích là:
Quá trình đẳng tích là quá trình biến đổi trạng thái khi thể tích không đổi
Hệ thức nào sau đây không phải là hệ thức của định luật Sác-lơ?
Ta có: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.
\(p \sim T \to \frac{p}{T} = h/s\)
=>Phương án B sai
Hiện tượng có liên quan đến định luật Sác-lơ là:
Ta có: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.
Biểu diễn hai đường đẳng tích của cùng một khối lượng không khí trong hệ tọa độ \(\left( {p-T} \right)\). Mối quan hệ đúng về các thể tích \({V_1},{V_2}\) là:
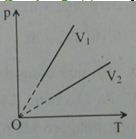
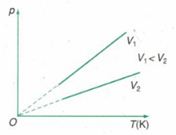
Đường đẳng tích là:
Đường biểu diễn sự biến thiên của áp suất theo nhiệt độ khi thể tích không đổi gọi là đường đẳng tích.
Trong hệ tọa độ (p,T), đường đẳng tích là:
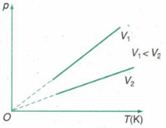
Trong hệ tọa độ (p,T) đường đẳng tích là đường thẳng mà nếu kéo dài sẽ đi qua gốc tọa độ.
Xét một quá trình đẳng tích của một lượng khí lí tưởng nhất định. Tìm phát biểu sai.
A, B, C - đúng
D - sai vì: \(p \sim T\)
\({t_1},{\rm{ }}{t_2}\) là trị số của hai nhiệt độ trong nhiệt giai Celsius. \({T_1},{T_2}\) là trị số của hai nhiệt độ ấy trong nhiệt giai tuyệt đối. Hệ thức đúng là:
Ta có: \(T = t + 273\)
\({T_2}-{T_1} = {t_2}-{t_1}\)
\( \to {T_1} = {T_2}-{t_2} + {t_1}\)
Một bóng đèn có nhiệt độ khi tắt là \({25^0}C\), khi sáng là \({323^0}C\), thì áp suất của khí trơ trong bóng đèn tăng lên là:
Vì thể tích của bóng đèn không đổi nên ta có:
\(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \to \frac{{{p_2}}}{{{p_1}}} = \frac{{{T_2}}}{{{T_1}}} = \frac{{323 + 273}}{{25 + 273}} = 2\) lần
Khi đung nóng một bình kín chứa khí để nhiệt độ tăng \({1^0}C\) thì áp suất khí tăng thêm \(\frac{1}{{360}}\) áp suất ban đầu. Nhiệt độ ban đầu của khí là:
Ta có:
- Trạng thái 1: \({p_1} = p,{T_1} = t + 273\)
- Trạng thái 2: \({p_2} = p\left( {1 + \frac{1}{{360}}} \right),{T_2} = t + 1 + 273\)
Do thể tích không đổi, theo định luật Sáclơ, ta có:
\(\begin{array}{l}\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \leftrightarrow \frac{p}{{t + 273}} = \frac{{p\left( {1 + \frac{1}{{360}}} \right)}}{{t + 1 + 273}}\\ \to t = {87^0}C\end{array}\)
Một săm xe được bơm căng không khí có áp suất \(2{\rm{a}}tm\) và nhiệt độ \({20^0}C\). Săm xe chịu được áp suất lớn nhất là \(2,4atm\), hỏi săm xe có bị nổ không khi nhiệt độ bên trong săm tăng lên đến \({42^0}C\)?
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 20 + 273 = 293K\\{p_1} = 2{\rm{a}}tm\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = 42 + 273 = 315K\\{p_2} = ?\end{array} \right.\)
Áp dụng biểu thức định luật Sáclơ, ta có:
\(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \to {p_2} = {T_2}\frac{{{p_1}}}{{{T_1}}} = 315\frac{2}{{293}} = 2,15{\rm{a}}tm\)
Nhận thấy: \({p_2} < {p_{max}} \to \) bánh xe không bị nổ
Một bóng đèn dây tóc chưa sáng chứa khí lí tưởng ở nhiệt độ \({27^0}C\) khi bóng đèn phát sáng ở nhiệt độ \({105^0}C\) thì áp suất thay đổi một lượng là \(0,2{\rm{a}}tm\) tính áp suất bên trong bóng đèn trước khi thắp sáng.
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 27 + 273 = 300K\\{p_1}\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = 105 + 273 = 378K\\{p_2} = {p_1} + 0,2{\rm{a}}tm\end{array} \right.\)
Áp dụng biểu thức định luật Sáclơ, ta có:
\(\begin{array}{l}\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \leftrightarrow \frac{{{p_1}}}{{300}} = \frac{{{p_1} + 0,2}}{{378}}\\ \to {p_1} = 0,77{\rm{a}}tm\end{array}\)
Một nồi áp suất, bên trong là không khí ở \({23^0}C\) có áp suất bằng áp suất của không khí bên ngoài \(\left( {1{\rm{ }}atm} \right)\). Van bảo hiểm của nồi sẽ mở khi áp suất bên trong cao hơn áp suất bên ngoài \(1,2{\rm{ }}atm\). Nếu nồi được đung nóng tới \({160^0}C\) thì không khí trong nồi đã thoát ra chưa? Áp suất không khí trong nồi bằng bao nhiêu?
Lượng không khí trong nồi được đun nóng trong một quá trình đẳng tích.
Trạng thái 1: \(\left\{ \begin{gathered}
{t_1} = {\text{ }}{23^0}C \to {T_1} = 23 + 273 = 296K \hfill \\
{p_1} = {\text{ }}1{\text{ }}atm \hfill \\
\end{gathered} \right.\)
Trạng thái 2: $\left\{ \begin{gathered}
{t_1} = {160^0}C \to {T_1} = 160 + 273 = 433K{\text{ }} \hfill \\
{p_1} = ? \hfill \\
\end{gathered} \right.$
Trong quá trình đẳng tích:
\(\frac{{{p_2}}}{{{T_2}}} = \frac{{{p_1}}}{{{T_1}}} \to {p_2} = \frac{{{p_1}{T_2}}}{{{T_1}}} = \frac{{1.433}}{{296}} = 1,46{\rm{a}}tm\)
Áp suất này chỉ cao hơn áp suất bên ngoài \(0,46{\rm{ }}atm\)
=> Van bảo hiểm chưa mở, không khí trong nồi chưa thoát ra được.
Đồ thị nào sau đây biểu diễn quá trính đẳng tích:
đồ thị biểu diễn đường đẳng tích là đồ thị ở hình a.
Một khối khí lý tưởng thực hiện quá trình được biểu diễn như trên hình vẽ. Đồ thị nào không biểu diễn đúng quá trình trên?
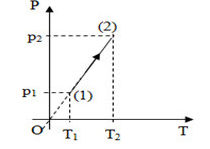
Qúa trình (1) -(2) là quá trình đẳng tích.
đồ thị không biểu diễn đường đẳng tích là đồ thị ở hình b.
Một khối khí lí tưởng thực hiện quá trình như hình vẽ.
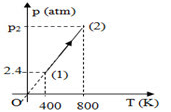
Các thông số được cho trên đồ thị, áp suất của khối khí khi kết thúc quá trình là:
Ta có:
Lượng không khí trong bình được đun nóng trong một quá trình đẳng tích.
Trạng thái 1: \(\left\{ \begin{array}{l}{t_1}\; = {\rm{ 400}}K\\{p_1}\; = {\rm{ 2,4 }}atm\end{array} \right.\) .
Trạng thái 2: \(\left\{ \begin{array}{l}{t_1}\; = 800K\\{p_2}\; = ?\end{array} \right.\)
Trong quá trình đẳng tích:
\(\dfrac{{{p_2}}}{{{T_2}}} = \dfrac{{{p_1}}}{{{T_1}}} \to {p_2} = \dfrac{{{p_1}{T_2}}}{{{T_1}}} = 4,8atm\)
Một bình được nạp khí ở nhiệt độ 300C dưới áp suất 360kPa. Sau đó bình được chuyển đến một nơi có nhiệt độ 400C, tính độ tăng áp suất của khí trong bình.
Áp dụng định luật Sác – lơ ta có:
\(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \dfrac{{{p_1}{T_2}}}{{{T_1}}} = \dfrac{{360.313}}{{303}} \approx 372kPa\)
Độ tăng áp suất của khí trong bình là:\(\Delta p = 372 - 360 = 12kPa\)