\(100g\) chì được truyền nhiệt lượng \(260J\) thì tăng nhiệt độ từ \({15^0}C\) lên đến \({35^0}C\). Nhiệt dung riêng của chì có giá trị là:
Ta có nhiệt lượng để chì tăng nhiệt độ từ \({15^0}C\) lên \({35^0}C\) là: \(Q = mc\Delta t = mc\left( {{t_2} - {t_1}} \right)\)
\( \Rightarrow c = \dfrac{Q}{{m\left( {{t_2} - {t_1}} \right)}} = \dfrac{{260}}{{0,1.\left( {35 - 15} \right)}} = 130J/kg.K\)
Để xác định nhiệt độ của một lò nung, người ta đưa vào trong lò một miếng sắt có khối lượng \(100g\). Khi miếng sắt có nhiệt độ bằng nhiệt độ của lò, người ta lấy ra và thả nó vào một nhiệt lượng kế chứa \(500g\) nước ở nhiệt độ \({20^0}C\). Khi đó nhiệt độ của nước tăng thêm \({10^0}C\), biết nhiệt dung riêng của sắt là \(478{\rm{ }}J/\left( {kg.K} \right)\), của nước là \(4180{\rm{ }}J/\left( {kg.K} \right)\). Nhiệt độ của lò xấp xỉ bằng:
Gọi \({t_1}\) - là nhiệt độ của lò nung (hay của miếng sắt đặt trong lò)
\({t_2} = {20^0}C\) là nhiệt độ ban đầu của nước
\(t\) - là nhiệt độ cân bằng
Ta có, khi cân bằng nhiệt độ của nước tăng thêm \({10^0}C\)
Ta suy ra: \(t = 20 + 10 = {30^0}C\)
Ta có:
+ Nhiệt lượng do sắt tỏa ra: \({Q_1}\; = {\rm{ }}{m_1}{c_1}\left( {{t_1}\;-{\rm{ }}t} \right)\)
+ Nhiệt lượng do nước thu vào: \({Q_2}\; = {\rm{ }}{m_2}{c_2}\left( {t{\rm{ }}-{\rm{ }}{t_2}} \right)\)
+ Theo phương trình cân bằng nhiệt, ta có:
\(\begin{array}{l}\begin{array}{*{20}{l}}\begin{array}{l}{Q_1} = {Q_2}\\ \Leftrightarrow {m_1}{c_1}\left( {{t_1}-t} \right) = {m_2}{c_2}\left( {t-{t_2}} \right)\end{array}\\{ \Leftrightarrow 0,1.478.\left( {{t_1}-{\rm{30}}} \right) = 0,5.4180\left( {{\rm{30}}-20} \right)}\end{array}\\ \Rightarrow {t_1} \approx 467,{2^0}C\end{array}\)
Người ta bỏ 1 miếng hợp kim chì và kẽm có khối lượng \(150g\) ở \(t = {124^0}C\) vào 1 nhiệt lượng kế có nhiệt dung là \(50{\rm{ }}J/K\) chứa \(250g\) nước ở \({16^0}C\). Xác định khối lượng của kẽm và chì trong hợp kim trên, biết nhiệt độ khi cân bằng trong nhiệt lượng kế là \({18^0}C\). Bỏ qua sự trao đổi nhiệt với môi trường bên ngoài, \({C_{Zn}} = 337{\rm{ }}J/kg.K,{\rm{ }}{C_{Pb}} = 126{\rm{ }}J/Kg.K.\) của nước là \(4180{\rm{ }}J/\left( {kg.K} \right)\)
Gọi \({t_1}\) là nhiệt độ ban đầu của miếng hợp kim, ta có \({t_1} = {124^0}C\)
\({t_2}\) là nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế, ta có \({t_2} = {16^0}C\)
\(t = {32^0}C\) - nhiệt độ khi cân bằng trong nhiệt lượng kế
+ Nhiệt lượng toả ra:
\(\left\{ {\begin{array}{*{20}{l}}{{Q_{Zn}} = {\rm{ }}{m_{Zn}}.{C_{Zn}}\left( {{t_1}-t} \right) = {m_{Zn}}.337.\left( {124 - 18} \right) = 35722{m_{Zn}}}\\{{Q_{Pb}} = {m_{Pb}}.{C_{Pb}}\left( {{t_1}-t} \right) = {m_{Pb}}.126.\left( {124 - 18} \right) = 13356{m_{Pb}}}\end{array}} \right.\)
+ Nhiệt lượng thu vào:
\(\left\{ {\begin{array}{*{20}{l}}{{Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t-{t_2}} \right) = \dfrac{{250}}{{1000}}.4180\left( {18 - 16} \right) = 2090{\rm{ }}J}\\{{Q_{NLK}}{\rm{ }} = C'\left( {t-{t_2}} \right) = 50.\left( {18 - 16} \right) = 100J}\end{array}} \right.\)
+ Ta có, phương trình cân bằng nhiệt:
\(\begin{array}{l}{Q_{toa}} = {Q_{thu}}\\ \leftrightarrow \;35722{m_{Zn}} + 13356{m_{Pb}} = 2090 + \;100{\rm{ }}\left( 1 \right)\end{array}\)
Mặt khác, theo đầu bài, ta có: \({m_{Zn}} + {m_{Pb}} = 150g = 0,15kg{\rm{ }}\left( 2 \right)\)
Từ (1) và (2), ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}35722{m_{Zn}} + 13356{m_{Pb}} = 2190\\{m_{Zn}} + {m_{Pb}} = 0,15\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{m_{Zn}} \approx {8.10^{ - 3}}kg\\{m_{Pb}} = 0,142kg\end{array} \right.\end{array}\)
Để xác định nhiệt độ của 1 cái lò, người ta đưa vào một miếng sắt \(m = 16g\). Khi miếng sắt có nhiệt độ bằng nhiệt độ của lò, người ta lấy ra và thả ngay vào nhiệt lượng kế chứa \(600g\) nước ở \({10^0}C\), nhiệt độ của nước tăng lên tới \({20^0}C\). Xác định nhiệt độ của lò. Biết nhiệt dung riêng của sắt là \(478{\rm{ }}J/\left( {kg.K} \right)\), của nước là \(4180{\rm{ }}J/\left( {kg.K} \right)\).
+ Nhiệt lượng tỏa ra:
\(\begin{array}{l}{Q_{Fe}} = {m_{Fe}}.{C_{Fe}}\left( {{t_2}-t} \right) = \dfrac{{16}}{{1000}}.478.\left( {{t_2} - 20} \right)\\ = 7,648{t_2}-152,96\end{array}\)
+ Nhiệt lượng thu vào:
\(\begin{array}{l}{Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t-{t_1}} \right) = \dfrac{{600}}{{1000}}.4180\left( {20 - 10} \right)\\ = 25080J\end{array}\)
+ Áp dụng phương trình cân bằng ta có:
\(\begin{array}{*{20}{l}}{{Q_{toa}}{\rm{ }} = {Q_{thu}}}\\{\; \leftrightarrow 7,648{t_2}-152,96 = 25080}\\{\; \to {t_{2{\rm{ }}}} = 3299,{3^0}C}\end{array}\)
Một bình nhôm khối lượng \(0,5kg\) chứa \(4kg\) nước ở nhiệt độ \({20^0}C\). Người ta thả vào bình một miếng sắt có khối lượng \(0,2kg\) đã được nung nóng tới \({500^0}C\). Xác định nhiệt độ của nước khi bắt đầu có sự cân bằng nhiệt. Cho nhiệt dung riêng của nhôm là \(896J/kg.K\), của nước là \(4,{18.10^3}J/kg.K\), của sắt là \(0,{46.10^3}J/kg.K\).
Gọi \({t_1} = {20^0}C\) - nhiệt độ ban đầu của bình nhôm và nước trong bình nhôm
\({t_2} = {500^0}C\) - nhiệt độ của miếng sắt
\(t\) - nhiệt độ khi cân bằng của hệ
Ta có:
+ Nhiệt lượng do miếng sắt tỏa ra:
\(\begin{array}{l}{Q_{Fe}} = {m_{Fe}}.{C_{Fe}}\left( {{\rm{ }}{t_2}--t} \right)\\ = 0,2.0,{46.10^3}.\left( {500 - t} \right)\\ = 46000 - 92t\end{array}\)
+ Nhiệt lượng do bình nhôm và nước thu vào:
\(\begin{array}{l}{Q_{Al}} = {m_{Al}}.{C_{Al}}\left( {t--{t_1}} \right)\\ = 0,5.896.\left( {t - 20} \right)\\ = 448t - 8960\end{array}\)
\(\begin{array}{l}{Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t--{t_1}} \right)\\ = 4.4,{18.10^3}.\left( {t - 20} \right)\\ = 16720t - 334400\end{array}\)
Tổng nhiệt lượng thu vào:
\(\begin{array}{l}{Q_{thu}} = {Q_{Al}} + {Q_{{H_2}O}} = 448t - 8960 + 16720 - 334400\\ = 17168t - 343360\end{array}\)
+ Theo phương trình cân bằng nhiệt, ta có:
\(\begin{array}{l}{Q_{toa}} = {Q_{thu}}\\ \Leftrightarrow 46000 - 92t = 17168t - 343360\\ \Rightarrow t \approx 22,{6^0}C\end{array}\)
Thả một quả cầu nhôm \(m = 0,105kg\) được đun nóng tới \({142^0}C\) vào một cốc nước ở \({20^0}C\). Biết nhiệt độ khi có sự cân bằng nhiệt là \({42^0}C\). Tính khối lượng nước trong cốc, biết nhiệt dung riêng của \({C_{Al}} = 880{\rm{ }}J/kg.K\) và của nước \(\;{C_{{H_2}O}} = {\rm{ }}4200{\rm{ }}J/kg.K\) .
Ta có:
+ Nhiệt lượng do quả cầu bằng nhôm tỏa ra:
\(\begin{array}{l}{Q_1} = {m_{Al}}.{c_{Al}}.\left( {{t_1} - t} \right)\\ = 0,105.880.\left( {142 - 42} \right)\\ = 9240J\end{array}\)
+ Nhiệt lượng do nước thu vào là:
\(\begin{array}{l}{Q_2} = {m_{{H_2}O}}.{c_{{H_2}O}}\left( {t - {t_2}} \right)\\ = {m_{{H_2}O}}.4200.\left( {42 - 20} \right)\\ = 92400{m_{{H_2}O}}\end{array}\)
+ Theo phương trình cân bằng nhiệt ta có:
\(\begin{array}{l}{Q_1} = {Q_2}\\ \Leftrightarrow 9240 = 92400{m_{{H_2}O}}\\ \Rightarrow {m_{{H_2}O}} = 0,1kg = 100g\end{array}\)
Một nhiệt lượng kế bằng đồng khối lượng \({m_1} = 100g\) có chứa \({m_2} = 375g\) nước ở nhiệt độ \({25^0}C\). Cho vào nhiệt lượng kế một vật bằng kim loại khối lượng \({m_3} = 400g\) ở \({90^0}C\). Biết nhiệt độ khi có sự cân bằng nhiệt là \({30^0}C\). Tìm nhiệt dung riêng của miếng kim loại. Cho biết nhiệt dung riêng của đồng là \(380{\rm{ }}J/Kg.K\) , của nước là \(4200J/Kg.K\).
Gọi \({t_1} = {25^0}C\) - nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế
\({t_2} = {90^0}C\) - nhiệt độ của vật kim loại
\(t\) - nhiệt độ khi cân bằng của hệ
Ta có:
+ Nhiệt lượng mà nhiệt lượng kế và nước thu được:
\({Q_1} = {m_1}{c_1}\left( {t - {t_1}} \right)\)
\({Q_2} = {m_2}{c_2}\left( {t - {t_1}} \right)\)
=> tổng nhiệt lượng thu vào:
\(\begin{array}{l}{Q_{12}} = {Q_1} + {Q_2}\\ = \left( {{m_1}{c_1} + {m_2}{c_2}} \right)\left( {t - {t_1}} \right)\end{array}\)
+ Nhiệt lượng mà vật kim loại tỏa ra:
\({Q_3} = {m_3}{c_3}.\left( {{t_2} - t} \right)\)
Theo phương trình cân bằng nhiệt, ta có:
\(\begin{array}{l}{Q_3} = {Q_{12}}\\ \Leftrightarrow {m_3}{c_3}\left( {{t_2} - t} \right) = \left( {{m_1}{c_1} + {m_2}{c_2}} \right)\left( {t - {t_1}} \right)\\ \Rightarrow {c_3} = \dfrac{{\left( {{m_1}{c_1} + {m_2}{c_2}} \right)\left( {t - {t_1}} \right)}}{{{m_3}\left( {{t_2} - t} \right)}}\\ \Rightarrow {c_3} = \dfrac{{\left( {0,1.380 + 0,375.4200} \right)\left( {30 - 25} \right)}}{{0,4.\left( {90 - 30} \right)}}\\ \Rightarrow {c_3} = 336J/kg.K\end{array}\)
Một nhiệt lượng kế chứa \(2kg\) nước ở \({15^0}C\). Cho vào nhiệt lượng kế quả cân bằng đồng thau có khối lượng \(500g\) ở \({100^0}C\). Tìm nhiệt độ cân bằng của hệ. Coi rằng vỏ nhiệt lượng kế không thu nhiệt. Cho các nhiệt dung riêng của đồng là \({c_1} = 3,{68.10^2}J/kg.K\), nước là \({c_2} = 4,186kJ/kg.K\)
Gọi \({t_1} = {15^0}C\) - nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế
\({t_2} = {100^0}C\) - nhiệt độ của quả cân bằng đồng thau
\(t\) - nhiệt độ khi cân bằng của hệ
Ta có:
+ Nhiệt lượng do quả cân tỏa ra:
\(\begin{array}{l}{Q_{quacan}} = {m_{quacan}}.{c_1}\left( {{\rm{ }}{t_2}--t} \right)\\ = 0,5.3,{68.10^2}.\left( {100 - t} \right)\\ = 18400 - 184t\end{array}\)
+ Nhiệt lượng do nước thu vào:
\(\begin{array}{l}{Q_{{H_2}O}} = {m_{{H_2}O}}.{c_{{H_2}O}}\left( {t--{t_1}} \right)\\ = 2.4,{18.10^3}.\left( {t - 15} \right)\\ = 8360t - 125400\end{array}\)
+ Theo phương trình cân bằng nhiệt, ta có:
\(\begin{array}{l}{Q_{toa}} = {Q_{thu}}\\ \Leftrightarrow 18400 - 184t = 8360t - 125400\\ \Rightarrow t = 16,{8^0}C\end{array}\)
Một nhiệt lượng kế bằng đồng thau khối lượng \(128g\) chứa \(210g\) nước ở nhiệt độ \(8,{4^0}C\). Người ta thả một miếng kim loại khối lượng \(192g\) đã nung nóng tới \({100^0}C\) vào nhiệt lượng kế. Xác định nhiệt dung riêng của chất làm kim loại, biết nhiệt độ khi bắt đầu có sự cân bằng nhiệt là \(21,{5^0}C\). Cho nhiệt dung riêng của nước là \(4,{18.10^3}J/kg.K\), của đồng thau là \(0,{128.10^3}J/kg.K\)
Gọi \({t_1} = 8,{4^0}C\) - nhiệt độ ban đầu của bình nhôm và nước trong bình nhôm
\({t_2} = {100^0}C\) - nhiệt độ của miếng kim loại
\(t = 21,{5^0}C\) - nhiệt độ khi cân bằng của hệ
Ta có:
+ Nhiệt lượng do miếng kim loại tỏa ra:
\(\begin{array}{l}{Q_{KL}} = {m_{KL}}.{c_{KL}}\left( {{\rm{ }}{t_2}--t} \right)\\ = 0,192.{c_{KL}}.\left( {100 - 21,5} \right)\\ = 15,072{c_{KL}}\end{array}\)
+ Nhiệt lượng do nhiệt lượng kế và nước thu vào:
\(\begin{array}{l}{Q_{NLK}} = {m_{NLK}}.{c_{NLK}}\left( {t--{t_1}} \right)\\ = 0,128.0,{128.10^3}.\left( {21,5 - 8,4} \right)\\ = 214,63J\end{array}\)
\(\begin{array}{l}{Q_{{H_2}O}} = {m_{{H_2}O}}.{c_{{H_2}O}}\left( {t--{t_1}} \right)\\ = 0,21.4,{18.10^3}.\left( {21,5 - 8,4} \right)\\ = 11499,18J\end{array}\)
Tổng nhiệt lượng thu vào:
\({Q_{thu}} = {Q_{NLK}} + {Q_{{H_2}O}} = 214,63 + 11499,18 = 11713,81J\)
+ Theo phương trình cân bằng nhiệt, ta có:
\(\begin{array}{l}{Q_{toa}} = {Q_{thu}}\\ \Leftrightarrow 15,072{c_{KL}} = 11713,81\\ \Rightarrow {c_{KL}} = 777,19J/kg.K\end{array}\)
Để xác định nhiệt độ của một lò nung, người ta đưa vào trong lò một miếng sắt có khối lượng \(50{\rm{ }}g\). Khi miếng sắt có nhiệt độ bằng nhiệt độ của lò, người ta lấy ra và thả nó vào một nhiệt lượng kế chứa \(900{\rm{ }}g\) nước ở nhiệt độ \({17^0}C\). Khi đó nhiệt độ của nước tăng lên đến \({23^0}C\), biết nhiệt dung riêng của sắt là \(478{\rm{ }}J/\left( {kg.K} \right)\), của nước là \(4180{\rm{ }}J/\left( {kg.K} \right)\). Bỏ qua sự hấp thụ nhiệt của nhiệt lượng kế. Nhiệt độ của lò xấp xỉ bằng:
Gọi \(t_1\) - nhiệt độ của lò nung (cũng chính là nhiệt độ ban đầu của miếng sắt khi rút từ lò nung ra), \(t_2\) - nhiệt độ ban đầu của nước, \(t\) - nhiệt độ khi cân bằng
Ta có:
+ Nhiệt lượng do sắt tỏa ra: \({Q_1} = {\text{ }}{m_1}{c_1}\left( {{t_1}-{\text{ }}t} \right)\)
+ Nhiệt lượng do nước thu vào: \({Q_2} = {\text{ }}{m_2}{c_2}\left( {t{\text{ }}-{\text{ }}{t_2}} \right)\)
Theo phương trình cân bằng nhiệt ta có:
\(\begin{gathered}\begin{array}{*{20}{l}}
{{Q_1} = {Q_2} \leftrightarrow {m_1}{c_1}\left( {{t_1}-{\text{ }}t} \right){\text{ }} = {\text{ }}{m_2}{c_2}\left( {t{\text{ }}-{\text{ }}{t_2}} \right)} \\ { \leftrightarrow 0,05.478\left( {{t_1}-{\text{ }}23} \right) = 0,9.4180\left( {23{\text{ }}-{\text{}}17} \right)}
\end{array} \hfill \\
\to {t_1} \approx {\text{ }}{967^0C} \hfill \\
\end{gathered} \)
Người ta bỏ 1 miếng hợp kim chì và kẽm có khối lượng \(50g\) ở \(t = {136^0}C\) vào 1 nhiệt lượng kế có nhiệt dung là \(50{\rm{ }}J/K\) chứa \(100g\) nước ở \({14^0}C\). Xác định khối lượng của kẽm và chì trong hợp kim trên, biết nhiệt độ khi cân bằng trong nhiệt lượng kế là \({18^0}C\). Bỏ qua sự trao đổi nhiệt với môi trường bên ngoài, \({C_{Zn}} = 337{\rm{ }}J/kg.K,{\rm{ }}{C_{Pb}} = 126{\rm{ }}J/Kg.K.\) của nước là \(4180{\rm{ }}J/\left( {kg.K} \right)\)
Gọi \({t_1}\) là nhiệt độ ban đầu của miếng hợp kim, ta có \({t_1} = {136^0}C\)
\({t_2}\) là nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế, ta có \({t_2} = {14^0}C\)
\(t = {18^0}C\) - nhiệt độ khi cân bằng trong nhiệt lượng kế
+ Nhiệt lượng toả ra:
\(\left\{ {\begin{array}{*{20}{l}}{{Q_{Zn}} = {\rm{ }}{m_{Zn}}.{C_{Zn}}\left( {{t_1}-t} \right) = {m_{Zn}}.337.\left( {136 - 18} \right) = 39766{m_{Zn}}}\\{{Q_{Pb}} = {m_{Pb}}.{C_{Pb}}\left( {{t_1}-t} \right) = {m_{Pb}}.126.\left( {136 - 18} \right) = 14868{m_{Pb}}}\end{array}} \right.\)
+ Nhiệt lượng thu vào:
\(\left\{ {\begin{array}{*{20}{l}}{{Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t-{t_2}} \right) = \dfrac{{100}}{{1000}}.4180\left( {18 - 14} \right) = 1672{\rm{ }}J}\\{{Q_{NLK}}{\rm{ }} = C'\left( {t-{t_2}} \right) = 50.\left( {18 - 14} \right) = 200{\rm{ }}J}\end{array}} \right.\)
+ Ta có, phương trình cân bằng nhiệt:
\(\begin{array}{l}{Q_{toa}} = {Q_{thu}}\\ \leftrightarrow 39766{m_{Zn}} + 14868{m_{Pb}} = 1672 + 200{\rm{ }}\left( 1 \right)\end{array}\)
Mặt khác, theo đầu bài, ta có: \({m_{Zn}} + {m_{Pb}} = 50g=0,05kg{\rm{ }}\left( 2 \right)\)
Từ (1) và (2), ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}39766{m_{Zn}} + 14868{m_{Pb}} = 1872\\{m_{Zn}} + {m_{Pb}} = 0,05\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{m_{Zn}} = 0,045kg\\{m_{Pb}} = 4,{67.10^{ - 3}} \approx 0,005kg\end{array} \right.\end{array}\)
Để xác định nhiệt độ của 1 cái lò, người ta đưa vào một miếng sắt \(m = 22,3g\). Khi miếng sắt có nhiệt độ bằng nhiệt độ của lò, người ta lấy ra và thả ngay vào nhiệt lượng kế chứa \(450g\) nước ở \({15^0}C\), nhiệt độ của nước tăng lên tới \(22,{5^0}C\). Xác định nhiệt độ của lò. Biết nhiệt dung riêng của sắt là \(478{\rm{ }}J/\left( {kg.K} \right)\), của nước là \(4180{\rm{ }}J/\left( {kg.K} \right)\).
+ Nhiệt lượng tỏa ra:
\(\begin{array}{l}{Q_{Fe}} = {m_{Fe}}.{C_{Fe}}\left( {{t_2}-t} \right) = \dfrac{{22,3}}{{1000}}.478.\left( {{t_2} - 22,5}\right)\\ = 10,6594{t_2}-239,8365J\end{array}\)
+ Nhiệt lượng thu vào:
\(\begin{array}{l}{Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t-{t_1}} \right) = \dfrac{{450}}{{1000}}.4180\left( {22,5 - 15} \right)\\ = 14107,5{\rm{ }}J\end{array}\)
+ Áp dụng phương trình cân bằng ta có:
\(\begin{array}{*{20}{l}}
{{Q_{toa}}{\rm{ }} = {Q_{thu}}}\\
{ \leftrightarrow 10,6594{t_2}-239,8365 = 14107,5}\\
{ \to {t_{2{\rm{ }}}} = 1345,{98^0}C}
\end{array}\)
Một cốc nhôm \(m = 100g\) chứa \(300g\) nước ở nhiệt độ \({20^0}C\). Người ta thả vào cốc nước một thìa đồng khối lượng \(75g\) vừa rút ra từ nồi nước sôi \({100^0}C\). Xác định nhiệt độ của nước trong cốc khi có sự cân bằng nhiệt. Bỏ qua các hao phí nhiệt ra ngoài. Lấy
\({C_{Al}} = 880{\rm{ }}J/kg.K,{\rm{ }}{C_{Cu}} = 380{\rm{ }}J/kg.K,{C_{{H_2}O}} = {\rm{ }}4190{\rm{ }}J/kg.K\)
+ Nhiệt lượng tỏa ra:
\(\begin{array}{l}{Q_{Cu}} = {m_{Cu}}.{C_{Cu}}\left( {{\rm{ }}{t_2}-t} \right)\\ = \dfrac{{75}}{{1000}}.380.\left( {100 - t} \right)\\ = 2850-28,5tJ\end{array}\)
+ Nhiệt lượng thu vào:
\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t-{t_1}} \right)\\ = \dfrac{{300}}{{1000}}.4190.\left( {t - 20} \right)\\ = 1257.t-25140\end{array}\\\begin{array}{l}{Q_{Al}} = {m_{Al}}.{C_{Al}}\left( {t-{t_1}} \right)\\ = \dfrac{{100}}{{1000}}.880.\left( {t - 20} \right)\\ = 88.t - 1760\end{array}\end{array}} \right.\)
\(\begin{array}{*{20}{l}}{{Q_{toa}} = {Q_{thu}}}\\{ \leftrightarrow 2850-28,5t = 1257.t-25140 + 88.t - 1760}\\{ \to t{\rm{ }} = {\rm{ }}21,{7^0}C}\end{array}\)
Trộn 3 chất lỏng không tác dụng hoá học lẫn nhau. Biết \({m_1} = 1kg,{m_2} = 10kg,{m_3} = 5kg\), \({t_1} = 6^0C,{t_2} = - 40^0C,{t_3} = 60^0C\),\({C_1} = 2{\rm{ }}KJ/kg.K,{C_2} = 4KJ/kg.K,{C_3} = 2{\rm{ }}KJ/kg.K\). Tìm nhiệt độ khi cân bằng

Thả một quả cầu nhôm \(m = 0,15kg\) được đun nóng tới \({100^0}C\) vào một cốc nước ở \({20^0}C\). Sau một thời gian nhiệt độ của quả cầu và của nước đều bằng \({25^0}C\). Tính khối lượng nước, coi như chỉ có quả cầu và nước truyền nhiệt cho nhau,
\({C_{Al}} = 880{\rm{ }}J/kg.K,{C_{{H_2}O}} = {\rm{ }}4200{\rm{ }}J/kg.K\)
Nhiệt lượng tỏa ra
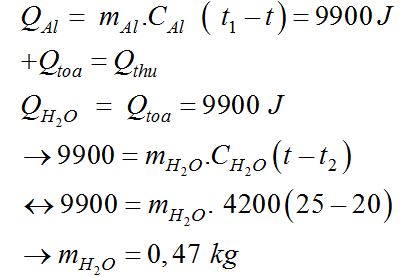
Để xác định nhiệt dung riêng của 1 kim loại, người ta bỏ vào nhiệt lượng kế chứa \(500g\) nước ở nhiệt độ \({15^0}C\) một miếng kim loại có \(m = 400g\) được đun nóng tới \({100^0}C\). Nhiệt độ khi có sự cân bằng nhiệt là \({20^0}C\). Tính nhiệt dung riêng của kim loại. Bỏ qua nhiệt lượng làm nóng nhiệt lượng kế và không khí. Lấy \({C_{{H_2}O}} = {\rm{ }}4190{\rm{ }}J/kg.K\).
Nhiệt lượng tỏa ra: \({Q_{Kl}} = {m_{Kl}}.{C_{Kl}}\left( {{t_2}-t} \right) = 0,4.{C_{Kl}}.\left( {100-20} \right) = 32.{C_{Kl}}\)
Nhiệt lượng thu vào: \({Q_{thu}} = {Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t-{t_1}} \right) = 10475{\rm{ }}J\)
Ta có:
\(\begin{array}{l}{Q_{toa}} = {Q_{thu}}\\ \Leftrightarrow 32{C_{Kl}} = 10475\\ \Rightarrow {C_{Kl}} = 327,34J/Kg.K\end{array}\)
Một ấm đun nước bằng nhôm có \(m = 350g\), chứa \(2,75kg\) nước được đun trên bếp. Khi nhận được nhiệt lượng \(650KJ\) thì ấm đạt đến nhiệt độ \({60^0}C\). Hỏi nhiệt độ ban đầu của ấm, biết \({C_{Al}} = 880{\rm{ }}J/kg.K,{C_{{H_2}O}} = 4190{\rm{ }}J/kg.K\)
Nhiệt lượng thu vào: \(\left\{ {\begin{array}{*{20}{l}}{{Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {t-{t_1}} \right) = 691350-11522,5{t_1}}\\{{Q_{Al}} = {m_{Al}}.{C_{Al}}\left( {t-{t_1}} \right) = 19320-322{t_1}}\end{array}} \right.\)
Nhiệt lượng ấm nhôm đựng nước nhận được:
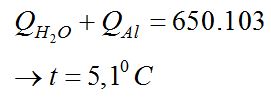
Để xác định nhiệt dung riêng của một chất lỏng, người ta đổ chất lỏng đó vào \(20g\) nước ở \({100^0}C\). Khi có sự cân bằng nhiệt, nhiệt độ của hỗn hợp nước là \({37,5^0}C\), \({m_{hh}} = 140g\). Biết nhiệt độ ban đầu của nó là \({20^0}C\) , \({C_{{H_2}O}} = {\rm{ }}4200{\rm{ }}J/kg.K\).
Nhiệt lượng tỏa ra:
\({Q_{{H_2}O}} = {m_{{H_2}O}}.{C_{{H_2}O}}\left( {{t_2}-t} \right) = 5250J\)
Nhiệt lượng thu vào: \({Q_{CL}} = {m_{CL}}.{C_{CL}}\left( {t-{t_1}} \right) = 2,1.{C_{CL}}\)
Qtỏa = Qthu
\(\begin{array}{*{20}{l}}{ \leftrightarrow 5250 = 2,1.{C_{CL}}}\\{ \to {C_{CL}}{\rm{ }} = {\rm{ }}2500{\rm{ }}J/Kg.K}\end{array}\)
Tính nhiệt lượng cần thiết để đun \(5kg\) nước từ \({15^0}C\) đến \({100^0}C\) trong một cái thùng bằng sắt có khối lượng \(1,5kg\). Biết nhiệt dung riêng của nước là \(4200J/kg.K\), của sắt là \(460J/kg.K\)
Gọi
- Khối lượng của thùng sắt \({m_1} = 1,5kg\), nhiệt dung riêng của thùng sắt là \({c_1} = 460J/kg.K\)
- Khối lượng của nước trong thùng sắt \({m_2} = 5kg\), nhiệt dung riêng của nước \({c_2} = 4200J/kg.K\)
Ta có:
+ Nhiệt độ ban đầu của thùng sắt và nước là \({t_1} = {15^0}C\)
+ Nhiệt độ cần đạt tới của nước và thùng sắt lúc sau \({t_2} = {100^0}C\)
+ Nhiệt lượng để cho thùng sắt có nhiệt độ tăng từ \({t_1} \Rightarrow {t_2}\) là: \({Q_1} = {m_1}{c_1}\left( {{t_2} - {t_1}} \right)\)
+ Nhiệt lượng để nước có nhiệt độ tăng từ \({t_1} \Rightarrow {t_2}\) là: \({Q_2} = {m_2}{c_2}\left( {{t_2} - {t_1}} \right)\)
=> Nhiệt lượng cần thiết để đun lượng nước đó từ \({15^0}C\) đến \({100^0}C\) là:
\(\begin{array}{l}Q = {Q_1} + {Q_2} = {m_1}{c_1}\left( {{t_2} - {t_1}} \right) + {m_2}{c_2}\left( {{t_2} - {t_1}} \right)\\ = \left( {{m_1}{c_1} + {m_2}{c_2}} \right)\left( {{t_2} - {t_1}} \right)\\ = \left( {1,5.460 + 5.4200} \right)\left( {100 - 15} \right)\\ = 1843650J\end{array}\)

