Trong bài thực hành đo gia tốc rơi tự do tại phòng thí nghiệm trường THPT Trần Quốc Tuấn, một học sinh có kết quả đo quãng đường vật rơi là \(798 \pm 1\,\left( {mm} \right)\) và thời gian rơi là \(0,404 \pm 0,005\,\left( s \right)\). Kết quả gia tốc rơi tự do của học sinh này là:
Ta có: \(\left\{ \begin{array}{l}l = 798 \pm 1\,\,\left( {mm} \right) = 0,798 \pm 0,001\,\left( m \right)\\t = 0,404 \pm 0,005\,\left( s \right)\end{array} \right.\)
Gia tốc rơi tự do trung bình:
\(g = \dfrac{{2\overline s }}{{{{\overline t }^2}}} = \dfrac{{2.0,798}}{{0,{{404}^2}}} = 9,78m/{s^2}\)
Sai số tỉ đối: \(\delta g = \dfrac{{\Delta g}}{{\overline g }} = \dfrac{{\Delta s}}{{\overline s }} + 2.\dfrac{{\Delta t}}{{\overline t }}\)
\( \Rightarrow \) Sai số tuyệt đối:
\(\begin{array}{l}\Delta g = \overline g .\left( {\dfrac{{\Delta s}}{{\overline s }} + 2.\dfrac{{\Delta t}}{{\overline t }}} \right)\\\,\,\,\,\,\,\, = 9,78.\left( {\dfrac{1}{{798}} + 2.\dfrac{{0,005}}{{0,404}}} \right) = 0,254m/{s^2}\end{array}\)
\( \Rightarrow \) Kết quả gia tốc rơi tự do của học sinh này là:
\(g = 9,78 \pm 0,254{\rm{ }}\left( {m/{s^2}} \right)\)
Chọn phát biểu sai ? Sai số dụng cụ \(\Delta A\) có thể
Phát biểu sai là: Sai số dụng cụ có thể loại trừ bằng cách hiệu chỉnh khi đo.
Dùng một thước milimet đo 5 lần khoảng cách s giữa hai điểm A,B đều cho một giá trị như nhau bằng 798mm. Tính sai số phép đo này và viết kết quả đo.
Lập bảng giá trị ta được:
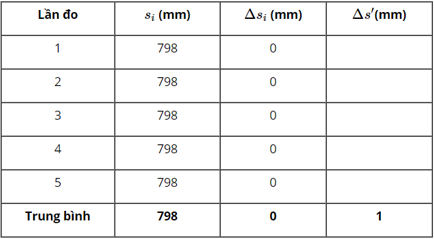
Giá trị trung bình của khoảng cách:
\(s=\dfrac{{{s}_{1}}+{{s}_{2}}+{{s}_{3}}+{{s}_{4}}+{{s}_{5}}}{5}=798mm\)
Sai số ngẫu nhiên:
\(\overline{\Delta s}=\frac{\Delta {{s}_{1}}+\Delta {{s}_{2}}+\Delta {{s}_{3}}+\Delta {{s}_{4}}+\Delta {{s}_{5}}}{5}=0mm\)
Sai số dụng cụ: \(\Delta s'=1mm\)
Sai số của phép đo: \(\Delta s=\overline{\Delta s}+\Delta s'=0+1=1mm\)
Kết quả đó: \(s=\overline{s}+\Delta s=798\pm 1\,\,\left( mm \right)\)
Có mấy cách để đo các đại lượng vật lí?
Có hai cách để đo các đại lượng vật lí là:
+ Đo trực tiếp : So sánh trực tiếp qua dụng cụ.
+ Đo gián tiếp : Đo một số đại lượng trực tiếp rồi suy ra đại lượng cần đo thông qua công thức.
Chọn phát biểu đúng. Trong hệ đơn vị SI, các đại lượng có đơn vị tương ứng là:
A- sai vì: trong hệ đơn vị SI, chiều dài có đơn vị là mét (m)
B- sai vì: trong hệ đơn vị SI, khối lượng có đơn vị là kilôgam (kg)
C- sai vì: trong hệ đơn vị SI, nhiệt độ có đơn vị là độ Kevin (K)
D - đúng
Đâu là cách viết kết quả đo đúng :
Cách viết kết quả đo đúng là: \(A = \overline A \pm \Delta A\)
Kết quả sai số tuyệt đối của một phép đo là \(0,0504\). Số chữ số có nghĩa là:
Trong kết quả: $0,0504\xrightarrow{{0,0\left[ {504} \right]}}$ 2 số 0 ở đầu không có nghĩa, số chữ số có nghĩa là \(3\)
Kết quả sai số tuyệt đối của một phép đo là \(1,02\). Số chữ số có nghĩa là:
Số chữ số có nghĩa trong kết quả: \(1,02\) là \(3\)
Để đo lực kéo về cực đại của một lò xo dao động với biên độ A ta chỉ cần dùng dụng cụ đo là:
Ta có:
+ Thước mét - đo chiều dài
+ Lực kế - đo lực
+ Đồng hồ - đo thời gian
+ Cân - đo khối lượng
=> Để đo lực kéo về cực đại của một lò xo dao động với biên độ A ta chỉ cần dùng dụng cụ đo là lực kế
Để xác định tốc độ trung bình của một người đi xe đạp chuyển động trên đoạn đường từ A đến B, ta cần dùng dụng cụ đo là:
+ Ta có, công dụng của các dụng cụ:
- Đồng hồ - đo thời gian
- Thước mét - đo chiều dài
- Tốc kế - đo vận tốc tức thời
+ Tốc độ trung bình của vật được xác định bởi biểu thức: \({v_{tb}} = \frac{S}{t}\)
=> để xác định được tốc độ trung bình, ta cần biết quãng đường mà người đó đi được trong khoảng thời gian t
=> Cần thước mét để đo chiều dài quãng đường người đó đi được và đồng hồ để đo thời gian người đó đi hết quãng đường đó.
Dùng một thước đo có chia độ đến milimét đo \(5\) lần khoảng cách \(d\) giữa hai điểm A và B đều cho cùng một giá trị \(1,245m\). Lấy sai số dụng cụ đo là một độ chia nhỏ nhất. Kết quả đo được viết:
Ta có:
+ Giá trị trung bình: \(d = 1,245m\)
+ Sai số ngẫu nhiên: \(\overline {\Delta d} = 0\)
+ Sai số hệ thống: \(\Delta d' = 1mm = 0,001m\)
=> Sai số của phép đo: \(\Delta d = \overline {\Delta d} + \Delta d' = 0 + 0,001 = 0,001m\)
=> Kết quả của phép đo: \(d = \left( {1,245 \pm 0,001} \right)m\)
Khi đo gia tốc rơi tự do, một học sinh tính được \(\overline g = 9,786\left( {m/{s^2}} \right)\) và \(\Delta g = 0,0259\left( {m/{s^2}} \right)\). Sai số tỉ đối của phép đo là:
Ta có, sai số tỉ đối của gia tốc rơi tự do: \(\delta g = \frac{{\Delta g}}{{\overline g }}.100\% = \frac{{0,0259}}{{9,786}}.100\% = 0,265\% \)
Một học sinh tiến hành thí nghiệm thực hành đo gia tốc rơi tự do thu được bảng số liệu như sau:
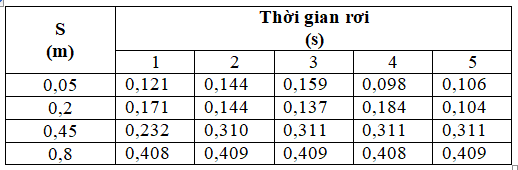
Bỏ qua sai số hệ thống. Gia tốc rơi tự do học sinh đó đo được có giá trị là:
Ta có:
+ Thời gian trung bình trong mỗi lần đo: \(\overline {{t_i}} = \frac{{{t_1} + {t_2} + {t_3} + {t_4} + {t_5}}}{5}\)
+ Gia tốc rơi tự do trong mỗi lần đo: \({g_i} = \frac{{2{\rm{S}}}}{{t_i^2}}\)
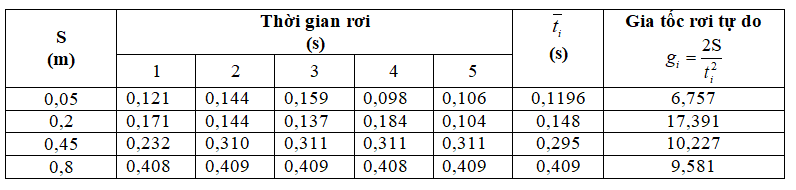
+ Gia tốc rơi tự do trung bình:
\(\begin{array}{l}\overline g = \frac{{{g_1} + {g_2} + {g_3} + {g_4}}}{4}\\ = \frac{{6,757 + 17,391 + 10,227 + 9,581}}{4}\\ = 10,989\left( {m/{s^2}} \right)\end{array}\)
+ Sai số trung bình:
\(\begin{array}{l}\overline {\Delta g} = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4}}}{4}\\ = \frac{{\left| {\overline g - {g_1}} \right| + \left| {\overline g - {g_2}} \right| + \left| {\overline g - {g_3}} \right| + \left| {\overline g - {g_4}} \right|}}{4}\\ = 2,82\left( {m/{s^2}} \right)\end{array}\)
=> Kết quả mà học sinh đó thu được là: \(g = \overline g + \overline {\Delta g} = \left( {10,989 \pm 2,82} \right)m/{s^2}\)
Một học sinh dùng đồng hồ bấm giây để đo chu kì dao động điều hòa của một con lắc lò xo. Sau 5 lần đo, xác định được khoảng thời gian Dt của môi dao động toàn phần như sau:

Bỏ qua sai số của của dụng cụ đo. Chu kì của con lắc là:
Chu kì trung bình: \(\overline T = \dfrac{{2,12 + 2,13 + 2,09 + 2,14 + 2,09}}{5} = 2,11s\)
Sai số tuyệt đối của từng lần đo: \(\left\{ \begin{array}{l}\Delta {T_1} = 0,01\\\Delta {T_2} = 0,02\\\Delta {T_3} = 0,02\\\Delta {T_4} = 0,03\\\Delta {T_5} = 0,02\end{array} \right.\)
Sai số tuyệt đối trung bình: \(\overline {\Delta T} = \dfrac{{0,01 + 0,02 + 0,02 + 0,03 + 0,02}}{5} = 0,02\)
Chu kì của con lắc là: \(T = \overline T \pm \overline {\Delta T} = 2,11 \pm 0,02s\)
Để đo gia tốc trọng trường g ở một nơi trên trên trái đất, người ta đã thả một viên bi rơi xuống một giếng sâu \(h = 495,21 \pm 0,5\,\,m\). Thời gian rơi của viên bi đo được là \(t = 10,05 \pm 0,01\,\,s\). Giá trị của gia tốc rơi tự do là
Giá trị trung bình của gia tốc trọng trường là: \(\overline g = \dfrac{{2\overline h }}{{{{\overline t }^2}}} = \dfrac{{2.495,21}}{{10,{{05}^2}}} = 9,81\,\,\left( {m/{s^2}} \right)\)
Sai số tuyệt đối của phép đo là: \(\Delta g = \overline g \left( {\dfrac{{\Delta h}}{{\overline h }} + 2\dfrac{{\Delta t}}{{\overline t }}} \right) = 9,81.\left( {\dfrac{{0,5}}{{495,21}} + 2.\dfrac{{0,01}}{{10,05}}} \right) = 0,03\,\,\left( {m/{s^2}} \right)\)
Giá trị của gia tốc rơi tự do là: \(g = 9,81 \pm 0,03\,\,\left( {m/{s^2}} \right)\)
Một học sinh dùng đùng đồng hồ bấm giây có độ chia nhỏ nhất là 0,01s và thước milimet có độ chia là 1mm để thực hành xác định gia tốc trọng trường tại điểm ở gần mặt đất. Sau ba lần thả vật ở ở độ cao h bất kỳ, kết quả thí nghiệm thu được như sau: h1 = 200cm; h2 = 250cm; h3 = 300cm; t1 = 0,64s; t2 = 0,72s; t3 = 0,78s. Bỏ qua sức cản không khí, cách viết đúng giá trị gia tốc trọng trường là:
Ta có: \(h = \frac{1}{2}g{t^2} \Rightarrow g = \frac{{2h}}{{{t^2}}}\)
Với:
\(\left\{ \begin{array}{l}
{h_1} = 200cm = 2m;{t_1} = 0,64s\\
{h_2} = 250cm = 2,5m;{t_2} = 0,72s\\
{h_3} = 300cm = 3m;{t_3} = 0,78s
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{g_1} = 9,77m/{s^2}\\
{g_2} = 9,65m/{s^2}\\
{g_3} = 9,86m/{s^2}
\end{array} \right.\)
Gia tốc trọng trường trung bình:
\(\bar g = \frac{{{g_1} + {g_2} + {g_3}}}{3} = 9,76m/{s^2}\)
Sai số tuyệt đối của từng lần đo:
\(\left\{ \begin{array}{l}
\Delta {g_1} = \left| {\bar g - {g_1}} \right|\\
\Delta {g_2} = \left| {\bar g - {g_2}} \right|\\
\Delta {g_3} = \left| {\bar g - {g_3}} \right|
\end{array} \right.\)
Sai số tuyệt đối trung bình:
\(\overline {\Delta g} = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3}}}{3} = 0,07m/{s^2}\)
Cách viết đúng giá trị của gia tốc trọng trường là:
\(g = 9,76{\rm{ }} \pm {\rm{ }}0,07\,\left( {m/{s^2}} \right)\)
Để xác định gia tốc của một chuyển động thẳng biến đổi đều, một học sinh đã sử dụng đồng hồ bấm giờ và thước mét để xác định thời gian t và đo quãng đường L sau đó xác định a bằng công thức \(L = a\dfrac{{{t^2}}}{2}\). Kết quả cho thấy \(L = \left( {2 \pm 0,005} \right)m\), \(t = \left( {4,2 \pm 0,2} \right)s\). Gia tốc a:
Ta có: \(L = a\dfrac{{{t^2}}}{2}\)
\( \Rightarrow a = \dfrac{{2L}}{{{t^2}}}\)
Gia tốc trung bình:
\(\overline a = \dfrac{{2\overline L }}{{{{\overline t }^2}}} = \dfrac{{2.2}}{{4,{2^2}}} = 0,227 \approx 0,23m/{s^2}\)
Lại có: \(\dfrac{{\Delta a}}{{\overline a }} = \dfrac{{\Delta L}}{{\overline L }} + 2\dfrac{{\Delta t}}{{\overline t }}\)
\( \Rightarrow \Delta a = \left( {\dfrac{{0,005}}{2} + 2\dfrac{{0,2}}{{4,2}}} \right).0,23 = 0,022m/{s^2}\)
\( \Rightarrow \) Gia tốc: \(a = \left( {0,23 \pm 0,02} \right)m/{s^2}\)

