Một học sinh tiến hành thí nghiệm thực hành đo gia tốc rơi tự do thu được bảng số liệu như sau:

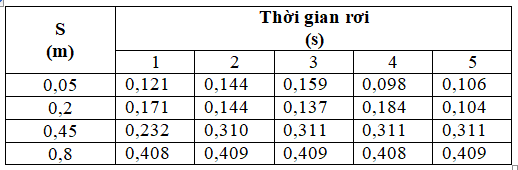
Bỏ qua sai số hệ thống. Gia tốc rơi tự do học sinh đó đo được có giá trị là:

Ta có:

+ Thời gian trung bình trong mỗi lần đo: \(\overline {{t_i}}  = \frac{{{t_1} + {t_2} + {t_3} + {t_4} + {t_5}}}{5}\)

+ Gia tốc rơi tự do trong mỗi lần đo: \({g_i} = \frac{{2{\rm{S}}}}{{t_i^2}}\)

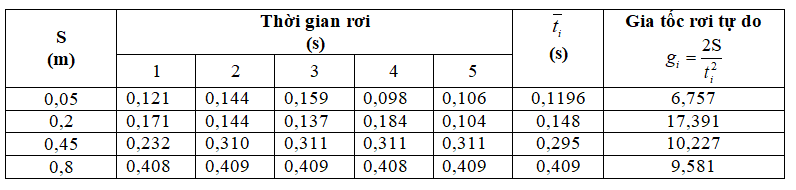
+ Gia tốc rơi tự do trung bình:

\(\begin{array}{l}\overline g  = \frac{{{g_1} + {g_2} + {g_3} + {g_4}}}{4}\\ = \frac{{6,757 + 17,391 + 10,227 + 9,581}}{4}\\ = 10,989\left( {m/{s^2}} \right)\end{array}\)

 + Sai số trung bình:

\(\begin{array}{l}\overline {\Delta g}  = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4}}}{4}\\ = \frac{{\left| {\overline g  - {g_1}} \right| + \left| {\overline g  - {g_2}} \right| + \left| {\overline g  - {g_3}} \right| + \left| {\overline g  - {g_4}} \right|}}{4}\\ = 2,82\left( {m/{s^2}} \right)\end{array}\)

 => Kết quả mà học sinh đó thu được là: \(g = \overline g  + \overline {\Delta g}  = \left( {10,989 \pm 2,82} \right)m/{s^2}\)