Đông lượng - Định luật bảo toàn động lượng

Chọn chiều dương là chiều chuyển động lúc sau của quả bóng.

Ta có: \(\Delta \overrightarrow p  = m{\overrightarrow v _2} - m\overrightarrow {{v_1}} \) .

Do \({\overrightarrow v _2} \uparrow  \downarrow {\overrightarrow v _1} =  > \Delta p = mv_2 - m(-v_1)= m\left( {{v_2} + {v_1}} \right) = 2\,kg.m/s\)

Ta có: \(\overrightarrow F .\Delta t = m.\Delta \overrightarrow v  =  > F\Delta t = m\left( {v - 0} \right) = 15\,N.s\)

Áp dụng biểu thức tính xung lượng của lực, ta có: \({\overrightarrow F _c}\Delta t = m\Delta \overrightarrow v\)

Do \({\overrightarrow v _2} \uparrow  \uparrow {\overrightarrow v _1}\)

\(=  > {F_c}.\Delta t = m\left( {{v_2} - {v_1}} \right)\)

\( =  > \,\left| {{F_c}} \right| = \dfrac{{m\left| {{v_2} - {v_1}} \right|}}{{\Delta t}} = \dfrac{{0,01\left| {300 - 600} \right|}}{{0,001}} = 3000\,N\)

Ta có:

\({\overrightarrow p _t} = {m_1}{\overrightarrow v _1} + {m_2}{\overrightarrow v _2}\)            

Do \({\overrightarrow v _2} \uparrow  \downarrow {\overrightarrow v _1} =  > {p_t} = {m_1}{v_1} - {m_2}{v_2} = 1.3 - 2.1,5 = 0\,kg.m/s\)

\(\overrightarrow {{p_t}}  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \)

Xét về mặt độ lớn, ta có:

\(\begin{array}{l}p_t^2 = p_1^2 + p_2^2 + 2{p_1}{p_2}cos\left( {\overrightarrow {{p_1}} ,\overrightarrow {{p_2}} } \right)\\ \leftrightarrow {10^2} = {6^2} + {8^2} + 2.6.8.cos\left( {\overrightarrow {{p_1}} ,\overrightarrow {{p_2}} } \right)\\ \to cos\left( {\overrightarrow {{p_1}} ,\overrightarrow {{p_2}} } \right) = 0 \to \left( {\widehat {\overrightarrow {{p_1}} ,\overrightarrow {{p_2}} }} \right) = {90^0}\\ \to \overrightarrow {{p_1}}  \bot \overrightarrow {{p_2}} \end{array}\)

A, B, C- đúng

D - sai

Hệ hai vật ngay khi va chạm mềm là một hệ kín nên động lượng của hệ được bảo toàn:

\({m_1}{\overrightarrow v _1} + {m_2}{\overrightarrow v _2} = \left( {{m_1} + {m_2}} \right)\overrightarrow v \)

Do \({v_2} = 0 =  > v = \frac{{{m_1}{v_1}}}{{{m_1} + {m_2}}} = \frac{{m.3}}{{m + 2m}} = 1\,m/s\)

Ta có:

+ Hệ viên đạn ( hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn

+ Gọi \(m_1 = 0,6m\) là khối lượng của mảnh thứ nhất

=> Khối lượng của mảnh còn lại là \(m_2=m-m_1=m-0,6m=0,4m\)

+ Áp dụng định luật bảo toàn động lượng ta có:

\(\overrightarrow p=\overrightarrow p_1 + \overrightarrow p_2\)

\(m\overrightarrow v  = {m_1}{\overrightarrow v _1} + \left( {m - {m_1}} \right){\overrightarrow v _2}\) (*)

Theo đầu bài, ta có mảnh 1 tiếp tục bay theo hướng cũ

=> \({\overrightarrow v _1} \uparrow  \uparrow \overrightarrow v\)

Từ phương trình (*) ta suy ra:

\({v_2} = \dfrac{{mv - {m_1}{v_1}}}{{m - {m_1}}} = \dfrac{{(10 - 25.0,6)m}}{{(1 - 0,6)m}} =  - 12,5\,m/s\)

Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.

Độ biến thiên động lượng của khí phụt ra trong giây đầu tiên:

\(\Delta p = mv = 1300.2500 = 3\,250\,000kg.m/s\)

Lực đẩy của tên lửa tại thời điểm đó:

\(F = \dfrac{{\Delta p}}{{\Delta t}} = \dfrac{{3\,250\,000}}{1} = 3,{25.10^6}N\)

Ta có độ lớn động lượng của vật 1 và vật hai là:

\(\left\{ \begin{array}{l}{p_1} = {m_1}.{v_1} = 1.3 = 3\,\,kg.m/s\\{p_2} = {m_2}.{v_2} = 3.1 = 3\,\,kg.m/s\end{array} \right.\)

Động lượng của hệ: \(\overrightarrow p  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \)

a) Do \(\overrightarrow {{v_1}} \, \uparrow  \uparrow \,\overrightarrow {{v_2}}  \Rightarrow p = {p_1} + {p_2} = 3 + 3 = 6\,\,\left( {kg.m/s} \right)\)

b) Do \(\overrightarrow {{v_1}} {\mkern 1mu}  \uparrow  \downarrow {\mkern 1mu} \overrightarrow {{v_2}}  \Rightarrow p = \left| {{p_1} - {p_2}} \right| = \left| {3 - 3} \right| = 0{\mkern 1mu} {\mkern 1mu} \left( {kg.m/s} \right)\)

c) Do \(\overrightarrow {{v_1}}  \bot \overrightarrow {{v_2}}  \Rightarrow p = \sqrt {p_1^2 + p_2^2}  = \sqrt {{3^2} + {3^2}}  = 3\sqrt 2 \,\,kg.m/s\)

Ta có: \(\overrightarrow a  = \dfrac{{\overrightarrow v  - \overrightarrow {{v_0}} }}{t} = \dfrac{{\overrightarrow v }}{t} \Rightarrow \overrightarrow v  = \overrightarrow a .t\)

Lại có: \(\overrightarrow a  = \dfrac{{\overrightarrow F }}{m} \Rightarrow \overrightarrow v  = \dfrac{{\overrightarrow F }}{m}.t\)

Động lượng: \(\overrightarrow p  = m.\overrightarrow v  = m.\dfrac{{\overrightarrow F }}{m}.t = \overrightarrow F .t\)

Chọn chiều dương là chiều chuyển động của viên đạn.

Áp dụng định luật bảo toàn động lượng cho hệ vật:  

\(\overrightarrow {{p_{tr}}} = \overrightarrow {{p_s}} \)

Ban đầu hệ đứng yên nên: \(\overrightarrow {{p_{tr}}} = 0\)

Ta có:

\(\begin{array}{l}
\overrightarrow {{p_{tr}}} = \overrightarrow {{p_s}} \Leftrightarrow 0 = m.\overrightarrow v + M.\overrightarrow V \\
\Rightarrow 0 = m.v - M.V \Leftrightarrow mv = M.V \Rightarrow V = \frac{{m.v}}{M} = \frac{{10.400}}{{4000}} = 1\left( {m/s} \right)
\end{array}\)

Khối lượng bi thép bằng ba lần khối lượng bi thuỷ tinh:  m₁ = 3.m₂

Động lượng của hệ trước va chạm: \(\overrightarrow {{p_1}}  = {m_1}\overrightarrow {{v_1}}  + {m_2}\overrightarrow {{v_2}}  = {m_1}\overrightarrow v  + {m_2}\overrightarrow 0  = {m_1}\overrightarrow v \)

Động lượng của hệ sau va chạm: \(\overrightarrow {{p_2}}  = {m_1}\overrightarrow {{v_1}'}  + {m_2}\overrightarrow {{v_2}'} \)

Áp dụng định luật bảo toàn động lượng cho lúc trước và sau va chạm ta có:

\(\overrightarrow {{p_1}}  = \overrightarrow {{p_2}}  \Leftrightarrow {m_1}\overrightarrow v  = {m_1}\overrightarrow {{v_1}}  + {m_2}\overrightarrow {{v_2}} \)

Chọn chiều dương là chiều chuyển động của bi thép trước khi va chạm. Ta có:

\({m_1}v = {m_1}{v_1}' + {m_2}{v_2}'\)

Theo bài ra ta có: \(\left\{ \begin{array}{l}{m_1}\; = 3.{m_2}\\{v_2}'\; = {\rm{ }}3.{v_1}'\end{array} \right. \Rightarrow 3{m_2}.v = 3.{m_2}.{v_1}'\; + {\rm{ }}{m_2}.3{v_1}' \Rightarrow \left\{ \begin{array}{l}{v_1}' = \dfrac{v}{2}\\{v_2}' = \dfrac{{3v}}{2}\end{array} \right.\)

\(\begin{array}{l}m = 1kg;v = 500m/s\\{m_1} = {m_2} = \dfrac{m}{2} = 0,5kg;{v_1} = 500\sqrt 2 m/s\end{array}\)

Xét hệ gồm hai mảnh đạn trong thời gian nổ.

Động lượng của hệ trước khi đạn nổ: \(\overrightarrow p  = m.\overrightarrow v \)

Động lượng sau khi đạn nổ: \(\overrightarrow {p'}  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}}  = {m_1}.\overrightarrow {{v_1}}  + {m_2}.\overrightarrow {{v_2}} \)

Áp dụng định luật bảo toàn động lượng ta có: \(\overrightarrow p  = \overrightarrow {p'}  \Rightarrow \overrightarrow p  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \)

Viên đạn đang bay theo phương thẳng đứng thì nổ thành hai mảnh mảnh thứ nhất bay theo phương ngang. Ta có hình vẽ:

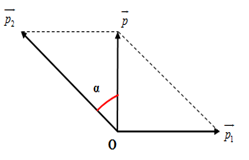
Từ hình vẽ ta có:

\(\begin{array}{l}p_2^2 = {p^2} + p_1^2 \Leftrightarrow {\left( {\dfrac{m}{2}.{v_2}} \right)^2} = {\left( {mv} \right)^2} + {\left( {\dfrac{m}{2}.{v_1}} \right)^2}\\ \Rightarrow v_2^2 = 4{v^2} + v_1^2 = {4.500^2} + {\left( {500\sqrt 2 } \right)^2} \Rightarrow {v_2} = 1225m/s\end{array}\)

Góc hợp bởi giữa \(\overrightarrow {{v_2}} \) và phương thẳng đứng là : \(\sin \alpha  = \dfrac{{{p_1}}}{{{p_2}}} = \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{500\sqrt 2 }}{{1225}} \Rightarrow \alpha  = {35^0}\)

Ta có: \(m = 1kg;{v_0} = 0;v = 5m/s;\Delta t = 10s\)

a) Gia tốc chuyển động của vật là:

\(a = \dfrac{{\Delta v}}{{\Delta t}} = \dfrac{{v - {v_0}}}{{\Delta t}} = \dfrac{{5 - 0}}{{10}} = 0,5m/{s^2}\)

b) Phương trình vận tốc:

\(v = {v_0} + at = 0 + at = 0,5.t\,\,\left( {m/s} \right)\)

Sau \(15s\) vận tốc của vật là:

\(v' = 0,5.15 = 7,5m/s\)

Độ lớn động lượng của vật sau \(15s\) là:

\(p = mv' = 1.7,5 = 7,5\;\left( {kg.m/s} \right)\)

Biểu thức động lượng \(\overrightarrow p  = m.\overrightarrow v \)

Khối lượng m đơn vị là kg, vận tốc v đơn vị là m/s

 \( \Rightarrow \) Động lượng \(\overrightarrow p \) có đơn vị là \(kg.m/s\)