Câu hỏi:
2 năm trước
Trên mặt một chiếc đồng hồ treo tường có kim giờ dài 15 cm, kim phút dài 20 cm. Lúc 12h hai kim trùng nhau, hỏi sau bao lâu hai kim trên lại trùng nhau
Trả lời bởi giáo viên
Đáp án đúng: c
R1 = 15cm; R2 = 20cm
Chu kì của kim giờ: T2 = 12h = 43200s
Chu kì của kim phút: T2 = 1h = 3600s
Tốc độ góc: \(\left\{ \begin{array}{l}{\omega _1} = \dfrac{{2\pi }}{{{T_1}}} \approx 1,{454.10^{ - 4}}\,\,rad/s\\{\omega _2} = \dfrac{{2\pi }}{{{T_2}}} \approx 1,{744.10^{ - 3}}\,\,rad/s\end{array} \right.\)
Lúc 12h hai kim trùng nhau.
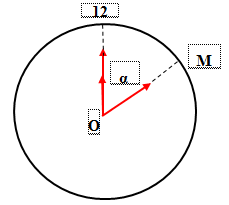
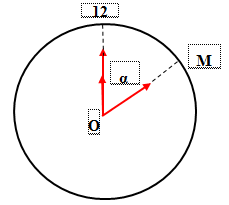
Ta có: \({\alpha _2} - {\alpha _1} = 2\pi \Leftrightarrow {\omega _2}t - {\omega _1}t = 2\pi \Rightarrow t = \dfrac{{2\pi }}{{{\omega _2} - {\omega _1}}} \approx 3928s \approx 1h5ph28s\)
Hướng dẫn giải:
Công thức tính tốc độ góc: \(\omega = \dfrac{{2\pi }}{T}\)

