Cho ba lực đồng quy tại O, đồng phẳng →F1,→F2,→F3 lần lượt hợp với trục Ox những góc 00,600,1200 và có độ lớn tương ứng là F1=F3=2F2=10N như hình vẽ. Tìm hợp lực của ba lực trên?
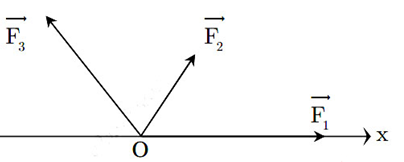
Cách 1:
Lực tổng hợp của ba lực: →F=→F1+→F2+→F3
Tổng hợp hai lực →F1,→F3 ta được →F13
{(^→F1;→F3)=1200F1=F3=10N
⇒F13=√F21+F23+2F1F3cos1200=10N
Và góc giữa →F13 với trục Ox là 600 (Δ có ba cạnh F1=F3=F13⇒Δ đều)
⇒→F=→F13+→F2
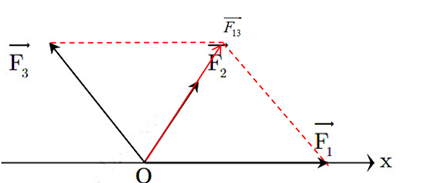
Lại có →F2 hợp với Ox một góc 600
⇒→F2↑↑→F13
⇒F=F13+F2=10+5=15N
Cách 2:
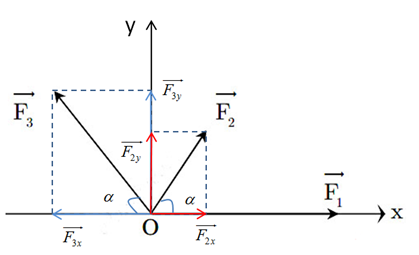
Ta có: F1=F3=2F2=10N
⇒{F1=10NF2=5NF3=10N
(Do đầu bài không có hình nên mình vẽ hướng của các lực như hình dưới nhé)
Phân tích các lực theo các phương Ox và Oy ta được:
{F2x=F2cosα=5.cos600=2,5NF2y=F2sinα=5.sin600=2,5√3N
{F3x=F3cosα=10.cos600=5NF3y=F3sinα=10.sin600=5√3N
Hợp lực theo các phương:
+ Phương Ox: →Fx=→F1+→F2x+→F3x
Chiếu ta được: Fx=F1+F2x−F3x=10+2,5−5=7,5N
+ Phương Oy: →Fy=→F2y+→F3y
Chiếu ta được: Fy=F2y+F3y=2,5√3+5√3=7,5√3N
Lực tổng hợp của 3 lực →F1,→F2,→F3 là : F=√F2x+F2y=√7,52+(7,5√3)2=15N
Một vật chịu tác dụng của ba lực như hình vẽ thì cân bằng:
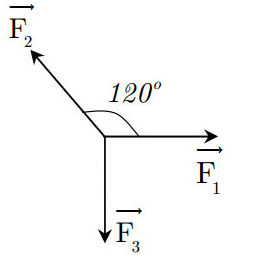
Biết rằng độ lớn của lực F3=40N. Hãy tính độ lớn của lực F1
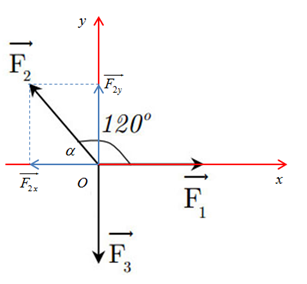
Gắn hệ trục tọa độ Oxy như hình vẽ
Phân tích →F2 thành 2 thành phần theo phương Ox và Oy như hình
Ta có vật cân bằng ⇒→F1+→F2+→F3=→0 (1)
Chiếu (1) lên các phương, ta được:
+ Ox: F1−F2x=0 (2)
+ Oy: F2y−F3=0 (3)
Mặt khác, ta có: α=1800−1200=600 và {F2x=F2cosαF2y=F2sinα
(3)⇔F2y=F3⇔F2sin600=40
⇒F2=40sin600=80√3N
(2)⇔F1=F2x=F2cosα=80√3.cos600=40√3N
Một chiếc đèn được treo vào tường nhờ một dây AB. Muốn cho đèn ở xa tường, người ta dùng một thanh chống nằm ngang một đầu tì vào tường, còn đầu kia tì vào điểm B của dây như hình vẽ:
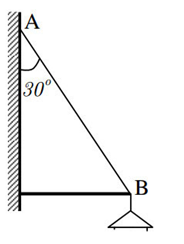
Biết đèn nặng 4kg và dây hợp với tường một góc 300 . Phản lực của thanh là bao nhiêu? Lấy g=10m/s2
Cho biết phản lực của thanh có phương dọc theo thanh.
+ Phân tích lực, ta được:
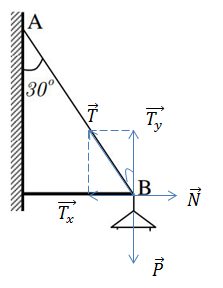
+ Theo điều kiện cân bằng của vật là hợp lực tác dụng lên vật bằng 0
Từ hình ta có:
+ →Ty cân bằng với trọng lực →P
↔Ty=P↔Tcos300=P→T=Pcos300=mgcos300=4.10√32=80√3(N)
+ →Tx cân bằng với phản lực →N
⇔Tx=N
Lại có: Tx=T.sin300
⇒N=T.sin300=80√3.sin300=40√3N
Hợp lực F của hai lực F1 và lực F2 có độ lớn 8√2N; lực F tạo với hướng của lực F1 góc 45° và F1 = 8 N. Xác định hướng và độ lớn của lực F2.
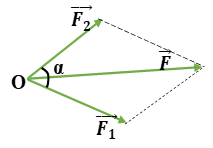
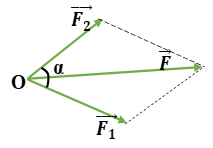
Ta có: {F=8√2NF1=8N(→F;→F1)=450⇒F1=F.cos450⇒→F2⊥→F1
→ Độ lớn của F2 là: F2=F.sin450=8√2.sin450=8N
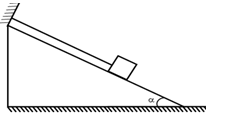
Một vật có khối lượng 2 kg được giữ yên trên một mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính. Biết α = 300. Cho g = 10 m/s2. Lực căng của dây treo có độ lớn là:
Chất điểm chịu tác dụng của các lực:
+ Trọng lực →P có độ lớn P = mg = 2.10 = 20N
+ Lực căng dây →T
+ Phản lực →Q
Biểu diễn các lực tác dụng vào vật trên hình vẽ:
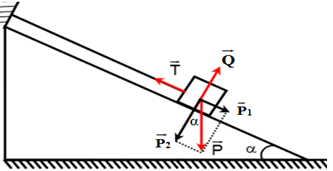
Phân tích →P=→P1+→P2 với: →P1 song song với mặt phẳng nghiêng; →P2 vuông góc với mặt phẳng nghiêng.
Điều kiện cân bằng của chất điểm: →T+→Q+→P1+→P2=0
Xét theo hai phương song song và vuông góc với mặt phẳng nghiêng: {→T+→P1=0→Q+→P2=0⇒{T=P1Q=P2
Từ hình vẽ ta có: {P1=P.sinαP2=P.cosα⇒{T=P1=P.sinα=20.sin30=10NQ=P2=P.cosα=20.cos30=10√3N
Lực là:
Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.
Chọn phát biểu đúng?
Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.
Chọn phát biểu đúng. Tổng hợp lực:
Hợp lực là thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt các lực ấy.
Khi nói về phép phân tích lực, phát biểu nào sau đây sai?
Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.
Các lực thay thế gọi là các lực thành phần
A, B, C - đúng
D - sai
Một chất điểm chịu tác dụng đồng thời của hai lực thành phần có độ lớn F1 và F2 thì hợp lực F của chúng luôn có độ lớn thỏa mãn hệ thức:
|F1−F2|≤F≤F1+F2
Hai lực đồng quy →F1 và →F2 hợp với nhau một góc α, hợp lực của hai lực này có độ lớn là:
F=√F12+F22+2F1F2cosα
Một chất điểm chịu tác dụng đồng thời của hai lực thành phần có độ lớn F1 và F2 thì hợp lực F của chúng luôn có độ lớn thỏa mãn hệ thức:
|F1−F2|≤F≤F1+F2
Hai lực đồng quy →F1 và →F2 hợp với nhau một góc 1800, hợp lực của hai lực này có độ lớn là:
Ta có hợp lực: F=√F12+F22+2F1F2cosα
Hai lực hợp với nhau một góc 1800 hay ngược chiều nhau
=> Hợp lực: F=|F1−F2|
Chọn câu đúng? Hợp lực của hai lực có độ lớn F và 2F có thể:
Gọi F’ là hợp lực của hai lực có độ lớn F và 2F
Ta có:
+ |F1−F2|≤F′≤F1+F2↔F<F′<3F
=> A, C - sai
+ Theo quy tắc hình bình hành ta có:
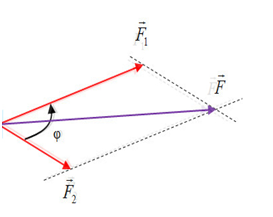
=> Hợp lực →F′ có thể vuông góc với lực có độ lớn nhỏ hơn là →F
=> B – đúng, D - sai
Hai lực có giá đồng quy có độ lớn 7N và 13N. Độ lớn hợp lực của hai lực này không thể có giá trị nào sau đây?
Ta có, hợp lực F
|F1−F2|≤F≤F1+F2↔13−7≤F≤13+7↔6N≤F≤20N
=> F không thể có giá trị là 22N
Hợp lực →F của hai lực đồng quy →F1 và →F2 có độ lớn phụ thuộc vào:
Ta có, hợp lực của hai lực thành phần F=√F12+F22+2F1F2cosα
=> F phụ thuộc vào:
+ Độ lớn của hai lực →F1 và →F2
+ Góc giữa hai lực →F1 và →F2
Các lực tác dụng lên một vật gọi là cân bằng khi:
Hợp của tất cả các lực tác lên vật gọi là cân bằng khi các lực tác dụng lên nó bằng →0
→F=→F1+→F2+...+→Fn=→0
Hai lực cân bằng không thể có:
Hai lực được gọi là cân bằng khi chúng có cùng phương, ngược chiều và cùng độ lớn.
=> Phương án A - sai
Hai lực có giá đồng quy có độ lớn F1=F2=10N có (→F1,→F2)=600. Hợp lực của hai lực này có độ lớn là:
Ta có, hợp lực của hai lực thành phần F=√F12+F22+2F1F2cosα
Thay số vào, ta được:
F=√F12+F22+2F1F2cosα=√102+102+2.10.10cos600=10√3N≈17,32N
Một chất điểm đứng yên dưới tác dụng của 3 lực 12N, 20N, 16N. Nếu bỏ lực 20N thì hợp lực của 2 lực còn lại có độ lớn bằng bao nhiêu ?
Ta có, ba lực 12N, 20N, 16N khi tác dụng vào vật mà vật đứng cân bằng thì hợp lực của chúng bằng 0
=> khi tác dụng bỏ lực 20N vào vật thì hợp lực của 2 lực còn lại đó có độ lớn chính bằng 20N

