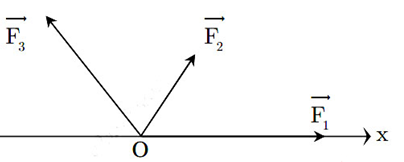
Cho ba lực đồng quy tại O, đồng phẳng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) lần lượt hợp với trục Ox những góc \({0^0},{60^0},{120^0}\) và có độ lớn tương ứng là \({F_1} = {F_3} = 2{F_2} = 10N\) như hình vẽ. Tìm hợp lực của ba lực trên?

Cách 1:

Lực tổng hợp của ba lực: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Tổng hợp hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_3}} \) ta được \(\overrightarrow {{F_{13}}} \)

\(\left\{ \begin{array}{l}\left( {\widehat {\overrightarrow {{F_1}} ;\overrightarrow {{F_3}} }} \right) = {120^0}\\{F_1} = {F_3} = 10N\end{array} \right.\)

\( \Rightarrow {F_{13}} = \sqrt {F_1^2 + F_3^2 + 2{F_1}{F_3}cos{{120}^0}}  = 10N\)

Và góc giữa \(\overrightarrow {{F_{13}}} \) với trục Ox là \({60^0}\) (\(\Delta \) có ba cạnh \({F_1} = {F_3} = {F_{13}} \Rightarrow \Delta \) đều)

\( \Rightarrow \overrightarrow F  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_2}} \)

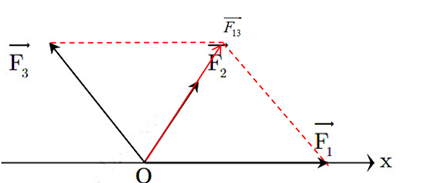
Lại có \(\overrightarrow {{F_2}} \) hợp với Ox một góc \({60^0}\)

\( \Rightarrow \overrightarrow {{F_2}}  \uparrow  \uparrow \overrightarrow {{F_{13}}} \)

\( \Rightarrow F = {F_{13}} + {F_2} = 10 + 5 = 15N\)

Cách 2:

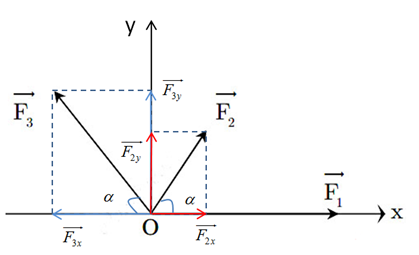
Ta có: \({F_1} = {F_3} = 2{F_2} = 10N\)

\( \Rightarrow \left\{ \begin{array}{l}{F_1} = 10N\\{F_2} = 5N\\{F_3} = 10N\end{array} \right.\)

(Do đầu bài không có hình nên mình vẽ hướng của các lực như hình dưới nhé)

Phân tích các lực theo các phương Ox và Oy ta được:

\(\left\{ \begin{array}{l}{F_{2x}} = {F_2}cos\alpha  = 5.cos{60^0} = 2,5N\\{F_{2y}} = {F_2}\sin \alpha  = 5.sin{60^0} = 2,5\sqrt 3 N\end{array} \right.\)

\(\left\{ \begin{array}{l}{F_{3x}} = {F_3}cos\alpha  = 10.cos{60^0} = 5N\\{F_{3y}} = {F_3}\sin \alpha  = 10.\sin {60^0} = 5\sqrt 3 N\end{array} \right.\)

Hợp lực theo các phương:

+ Phương Ox: \(\overrightarrow {{F_x}}  = \overrightarrow {{F_1}}  + \overrightarrow {{F_{2x}}}  + \overrightarrow {{F_{3x}}} \)

Chiếu ta được: \({F_x} = {F_1} + {F_{2x}} - {F_{3x}} = 10 + 2,5 - 5 = 7,5N\)

+ Phương Oy: \(\overrightarrow {{F_y}}  = \overrightarrow {{F_{2y}}}  + \overrightarrow {{F_{3y}}} \)

Chiếu ta được: \({F_y} = {F_{2y}} + {F_{3y}} = 2,5\sqrt 3  + 5\sqrt 3  = 7,5\sqrt 3 N\)

Lực tổng hợp của 3 lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) là : \(F = \sqrt {F_x^2 + F_y^2}  = \sqrt {7,{5^2} + {{\left( {7,5\sqrt 3 } \right)}^2}}  = 15N\)