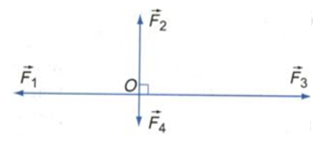
Một vật chịu tác dụng của ba lực như hình vẽ thì cân bằng:

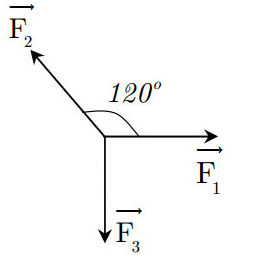
Biết rằng độ lớn của lực \({F_3} = 40N\). Hãy tính độ lớn của lực \({F_1}\)

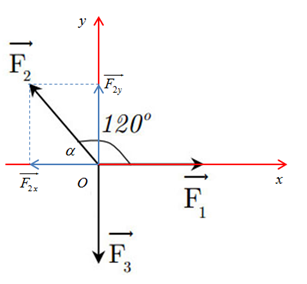
Gắn hệ trục tọa độ Oxy như hình vẽ

Phân tích \(\overrightarrow {{F_2}} \) thành 2 thành phần theo phương Ox và Oy như hình

Ta có vật cân bằng \( \Rightarrow \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \overrightarrow 0 \)  (1)

Chiếu (1) lên các phương, ta được:

+ Ox: \({F_1} - {F_{2x}} = 0\)  (2)

+ Oy: \({F_{2y}} - {F_3} = 0\) (3)

Mặt khác, ta có: \(\alpha  = {180^0} - {120^0} = {60^0}\)  và \(\left\{ \begin{array}{l}{F_{2x}} = {F_2}cos\alpha \\{F_{2y}} = {F_2}\sin \alpha \end{array} \right.\)

\(\left( 3 \right) \Leftrightarrow {F_{2y}} = {F_3} \Leftrightarrow {F_2}\sin {60^0} = 40\)

\( \Rightarrow {F_2} = \dfrac{{40}}{{\sin {{60}^0}}} = \dfrac{{80}}{{\sqrt 3 }}N\)

\(\left( 2 \right) \Leftrightarrow {F_1} = {F_{2x}} = {F_2}cos\alpha  = \dfrac{{80}}{{\sqrt 3 }}.cos{60^0} = \dfrac{{40}}{{\sqrt 3 }}N\)