Công của lực ma sát tác dụng lên vật đến khi dừng lại là

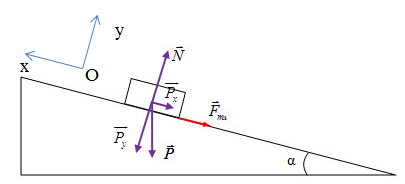
+ Theo định luật II – Newton, ta có: $\overrightarrow {{F_{ms}}}  + \overrightarrow N  + \overrightarrow P  = m\overrightarrow a$  (1)

Chọn chiều dương là chiều chuyển động của vật (vật đang chuyển động lên trên mặt phẳng nghiêng)

Gắn hệ trục tọa độ như hình

+ Chiếu (1) theo các phương ta được:

- Theo phương Oy: $N - {P_y} = 0 \Rightarrow N = {P_y} = Pcos\alpha$

- Theo phương Ox: $- {F_{ms}} - {P_x} = ma$ (2)

Ta có: $\left\{ \begin{array}{l}{F_{ms}} = \mu N = \mu P\cos \alpha  = 0,2.2.10.c{\rm{os3}}{{\rm{0}}^0} = 2\sqrt 3 N\\{P_x} = P\sin \alpha  = mg\sin \alpha  = 2.10.\sin {30^0} = 10N\end{array} \right.$

Thay vào (2) ta được:

$\begin{array}{l} - 2\sqrt 3  - 10 = ma\\ \Rightarrow a = \dfrac{{ - 2\sqrt 3  - 10}}{2} =  - 6,73m/{s^2}\end{array}$

+ Ta có vận tốc ban đầu của vật ${v_0} = 4m/s$, khi vật dừng lại $v = 0$

Áp dụng hệ thức liên hệ ta có: ${v^2} - v_0^2 = 2as$

=> Quãng đường mà vật đi được đến khi dừng lại là: $s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {4^2}}}{{2.\left( { - 6,73} \right)}} \approx 1,19m$

+ Góc hợp bởi lực ma sát và phương dịch chuyển của vật là ${180^0}$

=> Công của lực ma sát tác dụng lên vật: ${A_{{F_{ms}}}} = {F_{ms}}.s.cos{180^0} = 2\sqrt 3 .1,19.cos{180^0} =  - 4,12J$