Công của lực F khi vật chuyển động được \(5s\) là:

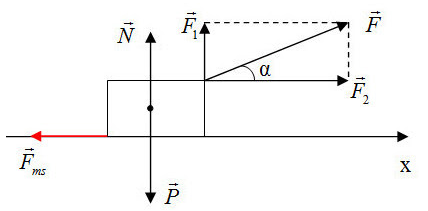
+ Chọn chiều dương là chiều chuyển động của vật

Theo định luật II – Newton ta có: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{ms}}}  = m\overrightarrow a \)  (1)

+ Chiếu (1) theo các phương, ta được:

- Theo phương Oy: \(N + {F_1} = P \Rightarrow N = P - {F_1}\)

Có \({F_1} = F\sin \alpha \)  ta suy ra \(N = P - F\sin \alpha \)

- Theo phương Ox: \({F_2} - {F_{ms}} = ma\)

Có \({F_2} = F\cos \alpha \), ta suy ra \(Fcos\alpha  - {F_{ms}} = ma\)

Lại có, lực ma sát \({F_{ms}} = \mu N = \mu \left( {P - F\sin \alpha } \right)\)

Ta suy ra:

\(\begin{array}{l}Fcos\alpha  - {F_{ms}} = ma\\ \Leftrightarrow Fcos\alpha  - \mu \left( {mg - F\sin \alpha } \right) = ma\\ \Leftrightarrow 10.cos{30^0} - 0,2.\left( {2.10 - 10.\sin {{30}^0}} \right) = 2.a\\ \Rightarrow a = 2,83m/{s^2}\end{array}\)

+ Quãng đường vật di chuyển được từ lúc ban đầu cho đến \(5s\) là: \(s = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}.2,{83.5^2} = 35,375m\)

+ Công của lực F khi vật chuyển động được 5s là: \({A_F} = Fs.c{\rm{os}}\alpha  = 10.35,375.cos{30^0} \approx 306,4J\)