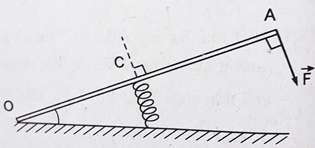
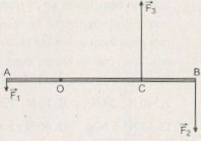
Một cái thước AB đặt trên mặt bàn nhẵn nằm ngang, có trục quay O cách đầu A một khoảng \(80cm\). Một lực \({F_1} = 10N\) tác dụng lên đầu A theo phương vuông góc với thước và lực thứ hai \(\overrightarrow {{F_2}} \) tác dụng lên điểm C của thước và theo phương vuông góc với thước (không vẽ trên hình) và cách A \(30cm\). Các lực đều nằm trên mặt phẳng nằm ngang. Nếu thước không chuyển động thì lực \(\overrightarrow {{F_2}} \) có hướng và độ lớn
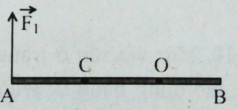
Trả lời bởi giáo viên
Ta có, 2 lực ở hai bên so với trục quay
Thước không chuyển động, nên:
+ Áp dụng quy tắc momen, ta có: \({M_{{F_1}}} = {M_{{F_2}}}\)
+ Mặt khác: \(\left\{ \begin{array}{l}{M_{{F_1}}} = {F_1}.AO\\{M_{{F_2}}} = {F_2}.CO\end{array} \right.\)
Ta suy ra:
\(\begin{array}{l}{F_1}.AO = {F_2}.CO\\ \to {F_2} = \dfrac{{{F_1}.AO}}{{CO}} = \dfrac{{10.0,8}}{{0,5}} = 16N\end{array}\)
Và \(\overrightarrow {{F_2}} \uparrow \downarrow \overrightarrow {{F_1}} \)
Hướng dẫn giải:
+ Vận dụng quy tắc momen: \({M_1} + {M_2} + ... = 0\)
+ Vận dụng biểu thức tính momen của lực: \(M = F{\rm{d}}\)