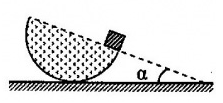
Bán cầu đồng chất khối lượng \(150g\). Trên mép bán cầu đặt một vật nhỏ khối lượng \(6,5g\). Hỏi mặt phẳng của bán cầu sẽ nghiêng góc \(\alpha \) bao nhiêu khi có cân bằng. Biết rằng trọng tâm bán cầu ở cách mặt phẳng của bán cầu một đoạn \(\dfrac{{3R}}{8}\) (R - bán kính bán cầu)
Trả lời bởi giáo viên
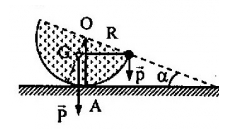
+ Các lực tác dụng lên bán cầu gồm: trọng lực \(\overrightarrow P \) (bán cầu), trọng lực \(\overrightarrow p \) (vật nhỏ), phản lực \(\overrightarrow Q \) (tại điểm tiếp xúc A)
+ Áp dụng quy tắc momen lực đối với trục quay qua O, ta có:
\({M_P} = {M_p}\) (vì \(\overrightarrow Q \) có giá đi qua trục quay tại A nên \({M_Q} = 0\))
+ Mặt khác, ta có: \(\left\{ \begin{array}{l}{M_P} = P.OG.\sin \alpha \\{M_p} = p.R.c{\rm{os}}\alpha \end{array} \right.\)
=> Ta suy ra:
\(\begin{array}{l}P.OG.\sin \alpha = p.R.c{\rm{os}}\alpha \\ \leftrightarrow Mg.\dfrac{{3R}}{8}\sin \alpha = mgRc{\rm{os}}\alpha \\ \to {\rm{M}}\dfrac{3}{8}\sin \alpha = mc{\rm{os}}\alpha \\ \to {\rm{tan}}\alpha {\rm{ = }}\dfrac{{8m}}{{3M}} = \dfrac{{8.6,5}}{{3.150}} = 0,12\\ \to \alpha = {7^0}\end{array}\)
Hướng dẫn giải:
+ Xác định các lực tác dụng lên bán cầu
+ Vận dụng quy tắc momen: \({M_1} + {M_2} + ... = 0\)
+ Vận dụng biểu thức tính momen của lực: \(M = F{\rm{d}}\)