Câu hỏi:
2 năm trước
Hai ô-tô chuyển động thẳng đều trên hai đoạn thẳng vuông góc với nhau. Vận tốc của ô-tô 1 là \(8m/s\), vận tốc của ô-tô 2 là \(6m/s\). Tính vận tốc của ô-tô 1 so với ô-tô 2
Trả lời bởi giáo viên
Đáp án đúng: d
(1) ô-tô 1
(2) ô-tô 2
(3) mặt đất
Ta có:
+ \({v_{13}} = 8m/s\)
+ \({v_{23}} = 6m/s\)
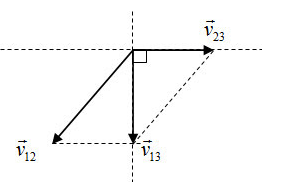
Từ hình ta suy ra: \({v_{12}} = \sqrt {v_{13}^2 + v_{23}^2} \)
\( \Rightarrow {v_{12}} = \sqrt {{8^2} + {6^2}} = 10m/s\)
Hướng dẫn giải:
Xác định các thông số:
+ Số 1: gắn với vật cần tính vận tốc
+ Số 2: gắn với hệ quy chiếu là các vật chuyển động
+ Số 3: gắn với hệ quy chiếu là các vật đứng yên
+ \({v_{12}}\): vận tốc của vật so với hệ quy chiếu chuyển động
+ \({v_{23}}\): vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu đứng yên
- Vận dụng công thức cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Câu hỏi khác
- Bài tập chuyển động thẳng đều lý 10 có lời giải
- Bài tập các khái niệm độ dời, quãng đường, vận tốc và gia tốc lý 10 có lời giải
- Bài tập các khái niệm cơ bản của chuyển động cơ học lý 10 có lời giải
- Bài tập chuyển động thẳng biến đổi đều lý 10 có lời giải
- Bài tập các dạng bài chuyển động thẳng biến đổi đều MÔN LÝ lớp 10
