Bài tập ôn tập chương 3

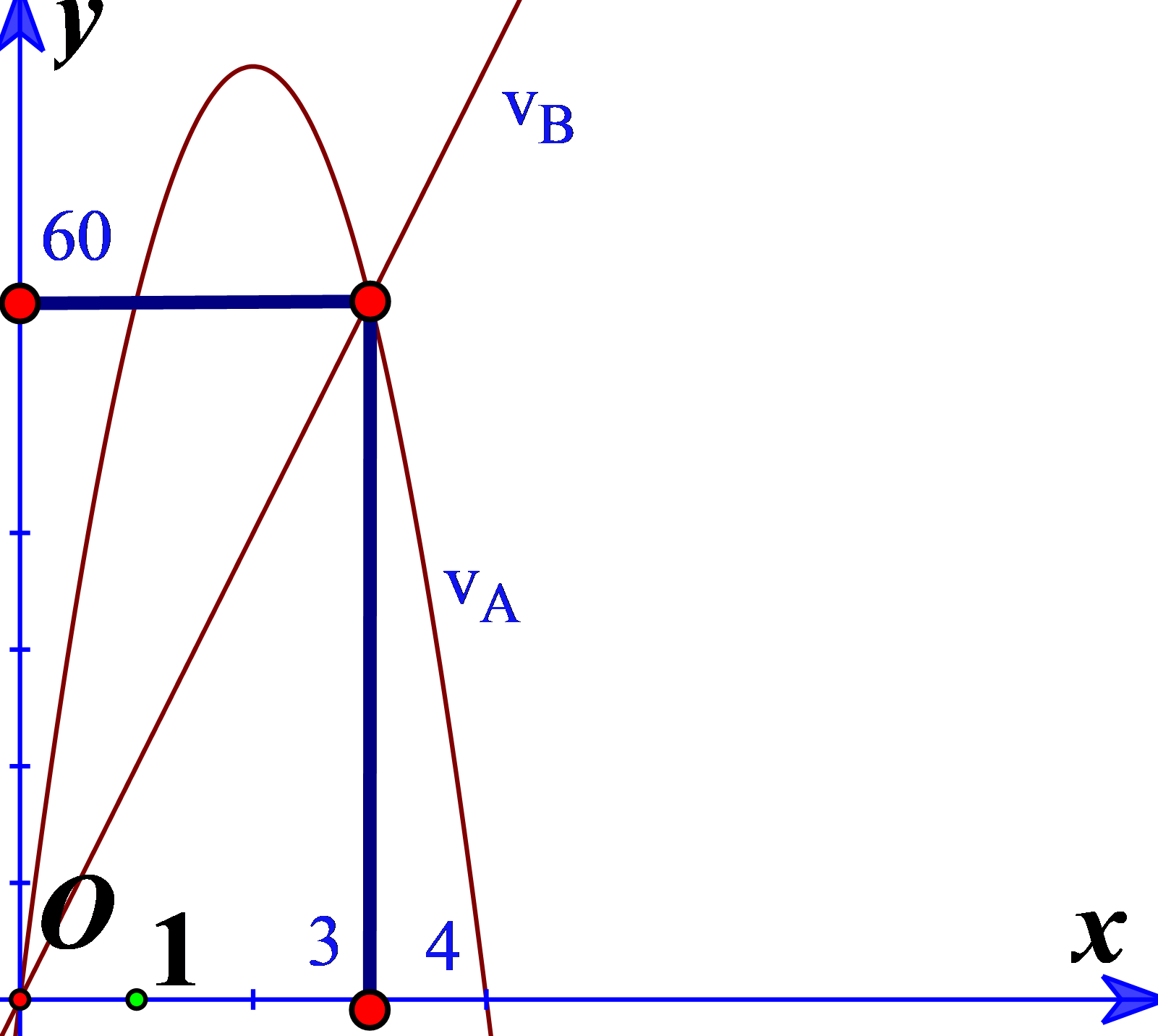
Bước 1: Biểu diễn vận tốc của xe A và xe B theo thời gian t. Dựa vào các điểm thuộc đồ thị và lập hệ tìm hệ số.

Biểu đồ biểu diễn vận tốc của xe $A$ là $(P):{v_A} = a{t^2} + bt + c(a \ne 0)$ đi qua điểm $(0;0);(3;60);(4;0) \Rightarrow {v_A} =  - 20{t^2} + 80t$.

Biểu thức biểu diễn vận tốc của xe $B$ là đường thẳng $\Delta :{v_B} = mt + n(m \ne 0)$ đi qua điểm $(0;0);(3;60) \Rightarrow {v_B} = 20t$.

Bước 2: Tính khoảng cách giữa hai xe sau 5 giây

Ta có ${v_A} =  - 20{t^2} + 80t = 0 \Rightarrow t = 4$ nên xe $A$ dừng lại sau giây thứ 4 . Do đó quãng đường xe $A$ đi được sau 4 giây là ${S_A} = \int_0^4 {\left( { - 20{t^2} + 80t} \right)} dt = \dfrac{{640}}{3}(m)$. Quāng đường xe $B$ đi được sau 5 giây đầu là ${S_B} = \int_0^5 {(20t)} dt = 250(m)$. Khoảng cách giữa hai xe sau 5 giây kể từ lúc xuất phát là $\Delta S = \left| {{S_A} - {S_B}} \right| = \dfrac{{110}}{3}(m)$.

Xét phương trình hoành độ giao điểm: ${x^2} = 2x \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.$

$\Rightarrow S = \int\limits_0^2 {\left| {{x^2} - 2x} \right|dx}  = \left| {\int\limits_0^2 {\left( {{x^2} - 2x} \right)dx} } \right| = \dfrac{4}{3}$

Dễ thấy các đáp án A, B, D đúng.

Đáp án C sai vì $f\left( {kx} \right) \ne k.f\left( x \right)$ , ví dụ ta lấy $k=2$.

Ta có:

$\begin{array}{l}f\left( x \right) = {x^2} \Rightarrow f\left( {2x} \right) = {\left( {2x} \right)^2} = {2^2}{x^2}\\2.f\left( x \right) = 2{x^2}\\ \Rightarrow f\left( {2x} \right) \ne 2.f\left( x \right)\end{array}$

$\int\limits_{}^{} {f\left( x \right)dx}  = \int\limits_{}^{} {\left( {{2^x} - \cos x + 1} \right)dx}  = \dfrac{{{2^x}}}{{\ln 2}} - \sin x + x + C$

Xét phương trình hoành độ giao điểm $2{x^2} - 4x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1 \notin \left[ { - 4; - 2} \right]\\x = 3 \notin \left[ { - 4; - 2} \right]\end{array} \right.$

$\Rightarrow S = \int\limits_{ - 4}^{ - 2} {\left| {2{x^2} - 4x - 6} \right|dx}  = \left| {\int\limits_{ - 4}^{ - 2} {\left( {2{x^2} - 4x - 6} \right)dx} } \right| = \dfrac{{148}}{3}$

Đặt $\left\{ \begin{array}{l}u = \cos x\\dv = {e^x}dx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}du =  - \sin xdx\\v = {e^x}\end{array} \right.$ $\Rightarrow I = {e^x}.\cos x + \int\limits_{}^{} {{e^x}\sin xdx}  + {C_1}$

Đặt $\left\{ \begin{array}{l}u = \sin x\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \cos xdx\\v = {e^x}\end{array} \right.$ $\Rightarrow \int\limits_{}^{} {{e^x}\sin xdx}  = {e^x}\sin x - \int\limits_{}^{} {{e^x}\cos xdx}  + {C_2}$

$\begin{array}{l} \Rightarrow I = {e^x}\cos x + {e^x}\sin x - I + C'\\ \Rightarrow 2I = {e^x}\cos x + {e^x}\sin x + C'\\ \Rightarrow I = \left( {\dfrac{1}{2}\cos x + \dfrac{1}{2}\sin x} \right){e^x} + C\\ \Rightarrow a = b = \dfrac{1}{2} \Rightarrow T = a + b = 1\end{array}$ 

Đặt $t = \sqrt {3x + 1}  \Leftrightarrow {t^2} = 3x + 1 \Leftrightarrow 2tdt = 3dx \Rightarrow dx = \dfrac{{2tdt}}{3}$ , đổi cận $\left\{ \begin{array}{l}x = 1 \Rightarrow t = 2\\x = 5 \Rightarrow t = 4\end{array} \right.$

$\begin{array}{l} \Rightarrow I = \int\limits_1^5 {\dfrac{{dx}}{{x\sqrt {3x + 1} }}}  = \int\limits_2^4 {\dfrac{{\dfrac{{2tdt}}{3}}}{{\dfrac{{{t^2} - 1}}{3}.t}}}  = 2\int\limits_2^4 {\dfrac{{dt}}{{{t^2} - 1}}}  = \int\limits_2^4 {\left( {\dfrac{1}{{t - 1}} - \dfrac{1}{{t + 1}}} \right)dt} \\\,\,\,\,\,\,\,\,\, = \left. {\ln \left| {\dfrac{{t - 1}}{{t + 1}}} \right|} \right|_2^4 = \ln \dfrac{3}{5} - \ln \dfrac{1}{3} = \ln 3 - \ln 5 + \ln 3 = 2\ln 3 - \ln 5\\ \Rightarrow \left\{ \begin{array}{l}a = 2\\b =  - 1\end{array} \right. \Rightarrow P = {a^2} + ab + 3{b^2} = {2^2} - 2 + 3{\left( { - 1} \right)^2} = 5.\end{array}$ 

$\int\limits_1^3 {\left[ {x - 2f\left( x \right)} \right]dx}  = \int\limits_1^3 {xdx}  - 2\int\limits_1^3 {f\left( x \right)dx}  = \left. {\dfrac{{{x^2}}}{2}} \right|_1^3 - 2.4 =  - 4$

Đặt $\left\{ \begin{array}{l}u = x\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = {e^x}\end{array} \right. \Rightarrow I = \left. {x.{e^x}} \right|_0^1 - \int\limits_0^1 {{e^x}dx}  = e - \left. {{e^x}} \right|_0^1 = e - \left( {e - 1} \right) = 1.$

Mệnh đề (I) và mệnh đề (IV) sai nên có 4 mệnh đề đúng.

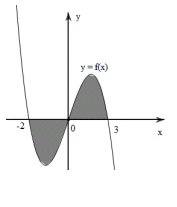
Ta thấy diện tích hình phẳng (phần tô đậm) được giới hạn bởi đồ thị hàm số $y = f\left( x \right),y = 0,x =  - 2,x = 3$, do đó $S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx}$ .

Dựa vào đồ thị hàm số ta thấy:

$\begin{array}{l}f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;3} \right) \Rightarrow \left| {f\left( x \right)} \right| = f\left( x \right)\,\,\forall x \in \left( {0;3} \right)\\f\left( x \right) < 0 \Leftrightarrow x \in \left( { - 2;0} \right) \Rightarrow \left| {f\left( x \right)} \right| =  - f\left( x \right)\,\,\forall x \in \left( { - 2;0} \right)\\ \Rightarrow S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx}  = \int\limits_{ - 2}^0 {\left| {f\left( x \right)} \right|dx}  + \int\limits_0^3 {\left| {f\left( x \right)} \right|dx}  =  - \int\limits_{ - 2}^0 {f\left( x \right)dx}  + \int\limits_0^3 {f\left( x \right)dx} \end{array}$

Đặt $t = \ln x \Rightarrow dt = \dfrac{{dx}}{x}$.

Đổi cận $\left\{ \begin{array}{l}x = 1 \Rightarrow t = 0\\x = e \Rightarrow t = 1\end{array} \right.$ .

$\Rightarrow I = \int\limits_0^1 {{t^2}dt}  = \left. {\dfrac{{{t^3}}}{3}} \right|_0^1 = \dfrac{1}{3}$

Ta có:

$\begin{array}{l}f\left( x \right) = \int\limits_{}^{} {f'\left( x \right)dx}  = \int\limits_{}^{} {\dfrac{1}{{2x - 1}}dx}  = \dfrac{1}{2}\ln \left| {2x - 1} \right| + C\\f\left( 1 \right) = \dfrac{1}{2}\ln 1 + C = 1 \Rightarrow C = 1\\ \Rightarrow f\left( x \right) = \dfrac{1}{2}\ln \left| {2x - 1} \right| + 1\\ \Rightarrow f\left( { - 5} \right) = \dfrac{1}{2}\ln 11 + 1 = 1 + \ln \sqrt {11} \end{array}$

Đặt  $t = \cos x \Leftrightarrow dt =  - \sin xdx$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = \pi  \Rightarrow t =  - 1\end{array} \right.$

$\Rightarrow I =  - \int\limits_1^{ - 1} {{t^3}dt}  = \int\limits_{ - 1}^1 {{t^3}dt}  = \left. {\dfrac{{{t^4}}}{4}} \right|_{ - 1}^1 = \dfrac{1}{4} - \dfrac{1}{4} = 0$

Đặt $t =  - x \Rightarrow x=-t \Rightarrow dx =  - dt$ , đổi cận $\left\{ \begin{array}{l}x =  3 \Rightarrow t = -3\\x = 0 \Rightarrow t = 0\end{array} \right.$

$\Rightarrow I =\int\limits_0^3 {f\left( x \right)dx} =  - \int\limits_0^{ - 3} {f\left( { - t} \right)dt}$$= \int\limits_{ - 3}^0 {f\left( { - t} \right)dt}  = \int\limits_{ - 3}^0 {f\left( { - x} \right)dx}$

Do $f\left( x \right)$ là hàm số chẵn $\Rightarrow f\left( { - x} \right) = f\left( x \right)\,\,\forall x \in TXD$.

$\Rightarrow I = \int\limits_{ - 3}^0 {f\left( x \right)dx}  = a.$

$\begin{array}{l}F\left( x \right) = \int\limits_{}^{} {f\left( x \right)dx}  \Rightarrow F'\left( x \right) = f\left( x \right)\\ \Rightarrow f\left( x \right) = F'\left( x \right) = 5{x^4} + 15{x^2} - 1\end{array}$

$\begin{array}{l}F\left( x \right) = \int\limits_{}^{} {f\left( x \right)dx}  = \int\limits_{}^{} {\sin 2xdx}  =  - \dfrac{{\cos 2x}}{2} + C\\F\left( 0 \right) =  - \dfrac{1}{2} + C = \dfrac{3}{2} \Rightarrow C = 2\\ \Rightarrow F\left( x \right) =  - \dfrac{{\cos 2x}}{2} + 2\\ \Rightarrow F\left( {\dfrac{\pi }{2}} \right) =  - \dfrac{{\cos \pi }}{2} + 2 = \dfrac{1}{2} + 2 = \dfrac{5}{2}\end{array}$

Ta có:

$\begin{array}{l}f\left( x \right) = \dfrac{{{x^3} - 2{x^2}}}{{{x^3}}} = 1 - \dfrac{2}{x}\\ \Rightarrow \int\limits_{}^{} {f\left( x \right)dx}  = x - 2\ln \left| x \right| + C\end{array}$

Đặt $t = \sqrt {1 + x}  \Rightarrow {t^2} = 1 + x \Leftrightarrow 2tdt = dx$.

Đổi cận $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 2 \Rightarrow t = \sqrt 3 \end{array} \right.$

$\Rightarrow I = \int\limits_1^{\sqrt 3 } {\dfrac{{{t^2} - 1}}{t}.2tdt}  = 2\int\limits_1^{\sqrt 3 } {\left( {{t^2} - 1} \right)dt}  = 2\left. {\left( {\dfrac{{{t^3}}}{3} - t} \right)} \right|_1^{\sqrt 3 } = 2\left( {\dfrac{{3\sqrt 3 }}{3} - \sqrt 3  - \dfrac{1}{3} + 1} \right) = \dfrac{4}{3}$

Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đồ thị hàm số $y = f\left( x \right)$, trục $Ox$  và hai đường thẳng $x = a,x = b\,\,\left( {a < b} \right)$ xung quanh trục $Ox$ là: $V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx$