Câu hỏi:
2 năm trước
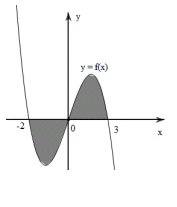
Cho đồ thị hàm số \(y = f\left( x \right)\). Diện tích S của hình phẳng (phần tô đậm trong hình dưới) là:
Trả lời bởi giáo viên
Đáp án đúng: c
Ta thấy diện tích hình phẳng (phần tô đậm) được giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = 0,x = - 2,x = 3\), do đó \(S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx} \) .
Dựa vào đồ thị hàm số ta thấy:
\(\begin{array}{l}f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;3} \right) \Rightarrow \left| {f\left( x \right)} \right| = f\left( x \right)\,\,\forall x \in \left( {0;3} \right)\\f\left( x \right) < 0 \Leftrightarrow x \in \left( { - 2;0} \right) \Rightarrow \left| {f\left( x \right)} \right| = - f\left( x \right)\,\,\forall x \in \left( { - 2;0} \right)\\ \Rightarrow S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^0 {\left| {f\left( x \right)} \right|dx} + \int\limits_0^3 {\left| {f\left( x \right)} \right|dx} = - \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^3 {f\left( x \right)dx} \end{array}\)
Hướng dẫn giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right),x = a,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
Xét dấu \(f\left( x \right) - g\left( x \right)\) trên từng khoảng xác định và phá dấu trị tuyệt đối.
Câu hỏi khác
- Bài tập nguyên hàm toán 12 có lời giải
- Bài tập tích phân các hàm số cơ bản toán 12 có lời giải
- Bài tập tích phân có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp đổi biến để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp từng phần để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
