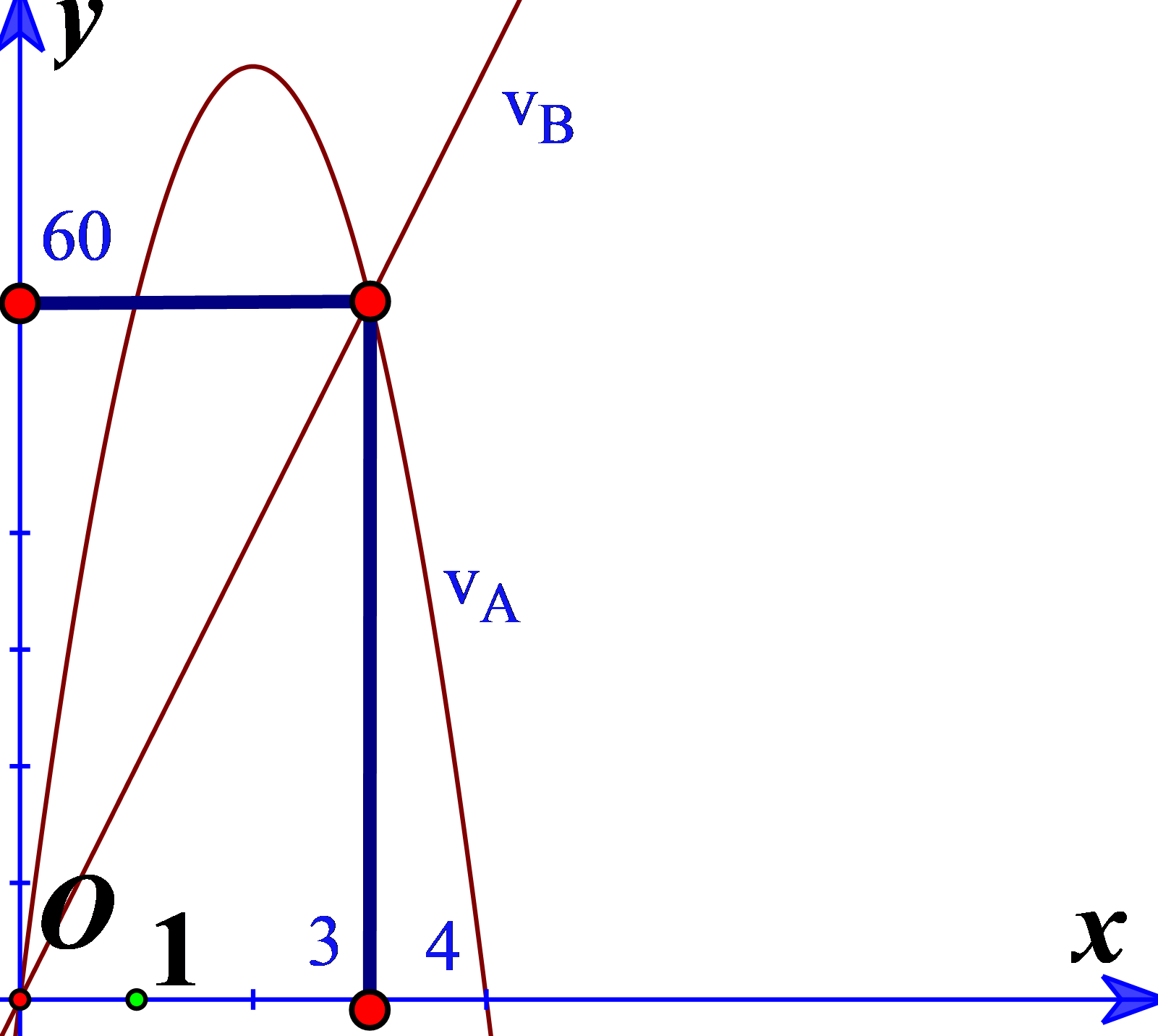
Cho đồ thị biểu diễn vận tốc của hai xe \(A\) và \(B\) khởi hành cùng một lúc và cùng vạch xuất phát, đi cùng chiều trên một con đường. Biết đồ thị biểu diễn vận tốc của xe \(A\) là một đường parabol và đồ thị biểu diễn vận tốc của xe \(B\) là một đường thẳng như hình vẽ bên. Hỏi sau 5 giây kể từ lúc xuất phát thì khoảng cách giữa hai xe là bao nhiêu mét? (Biết rằng xe \(A\) sẽ dừng lại khi vận tốc bằng 0 ).

\(S = \dfrac{{20}}{3}\)

\(S = \dfrac{{496}}{{15}}\)

\(S = \dfrac{4}{3}\)   

\(S = \dfrac{5}{3}\)

\(\int\limits_a^b {f\left( x \right)dx}  + \int\limits_b^c {f\left( x \right)dx}  = \int\limits_a^c {f\left( x \right)dx} \)                        

\(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx}  = \int\limits_a^b {f\left( x \right)dx}  + \int\limits_a^b {g\left( x \right)dx} \)

\(\int\limits_a^b {f\left( {k.x} \right)dx}  = k\int\limits_a^b {f\left( x \right)dx} \)                         

\(\int\limits_a^b {k.f\left( x \right)dx}  = k.\int\limits_a^b {f\left( x \right)dx} \)

\(\int\limits_{}^{} {f\left( x \right)dx}  = \dfrac{{{2^x}}}{{\ln 2}} + \sin x + x + C\)

\(\int\limits_{}^{} {f\left( x \right)dx}  = \dfrac{{{2^x}}}{{\ln 2}} - \sin x + x + C\)

\(\int\limits_{}^{} {f\left( x \right)dx}  = {2^x}.\ln 2 + \sin x + x + C\)      

\(\int\limits_{}^{} {f\left( x \right)dx}  = {2^x}.\ln 2 - \sin x + x + C\)

\(S = 8\)

\(S = \dfrac{{220}}{3}\)

\(S = \dfrac{{76}}{3}\)

\(S = \dfrac{{148}}{3}\)

\(T = \dfrac{1}{2}\)

\(T = 0\)

\(T = 1\)

\(T = 2\)

\(P = 11\)

\(P = 5\)

\(P = 2\)

\(P =  - 2\)