Khối tròn xoay tạo nên khi quay quanh trục \(Ox\) hình phẳng giới hạn bởi đồ thị hàm số \(y = 2x - {x^2}\) và trục \(Ox\) có thể tích
Xét phương trình hoành độ giao điểm \(2x - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
\( \Rightarrow V = \pi \int\limits_0^2 {{{\left( {2x - {x^2}} \right)}^2}dx} = \dfrac{{16}}{{15}}\pi \)
Nếu \(f\left( 4 \right) = 12;f'\left( x \right)\) liên tục và \(\int\limits_1^4 {f'\left( x \right)dx} = 17\). Tính \(f\left( 1 \right)?\)
\(\int\limits_1^4 {f'\left( x \right)dx} = 17 \Leftrightarrow f\left( 4 \right) - f\left( 1 \right) = 17 \Leftrightarrow 12 - f\left( 1 \right) = 17 \Rightarrow f\left( 1 \right) = - 5\)
Cho tích phân \(I = \int\limits_0^1 {x\left( {ax + b\sqrt {3{x^2} + 1} } \right)dx} = 3\), biết \(3b - 2a = 5\). Tính \(M = {a^2} - {b^2}.\)
$I = \int\limits_0^1 {x\left( {ax + b\sqrt {3{x^2} + 1} } \right)dx} = a\int\limits_0^1 {{x^2}dx} + b\int\limits_0^1 {x\sqrt {3{x^2} + 1} dx} = \left. {a\dfrac{{{x^3}}}{3}} \right|_0^1 + b{I_1} = \dfrac{a}{3} + b{I_1}$
Đặt \(t = \sqrt {3{x^2} + 1} \Rightarrow {t^2} = 3{x^2} + 1 \Leftrightarrow 2tdt = 6xdx \Rightarrow xdx = \dfrac{{tdt}}{3}\)
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 1 \Rightarrow t = 2\end{array} \right.\) , khi đó ${I_1} = \int\limits_1^2 {\dfrac{{tdt}}{3}.t} = \left. {\dfrac{1}{3}\dfrac{{{t^3}}}{3}} \right|_1^2 = \dfrac{8}{9} - \dfrac{1}{9} = \dfrac{7}{9}.$
\( \Rightarrow I = \dfrac{a}{3} + \dfrac{{7b}}{9} = 3\).
Khi đó ta có hệ phương trình $\left\{ \begin{array}{l}\dfrac{a}{3} + \dfrac{{7b}}{9} = 3\\3b - 2a = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right. \Rightarrow M = {a^2} - {b^2} = - 5$
Một xe mô tô phân khối lớn sau khi chờ đèn đỏ đã bắt đầu phóng nhanh với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường Parabol (hình vẽ). Biết rằng sau $15$ giây thì xe đạt đến vận tốc cao nhất $60{\rm{ }}m/s$ và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì quãng đường xe đi được là bao nhiêu?
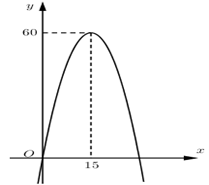
Gọi phương trình parabol biểu diễn cho vận tốc của vật là \(v\left( t \right) = a{t^2} + bt + c\,\,\left( {a \ne 0} \right)\)
Đỉnh của parabol có tọa độ \(\left( {15;60} \right) \Rightarrow - \dfrac{b}{{2a}} = 15\,\,\left( 1 \right)\)
Parabol đi qua điểm \(\left( {15;60} \right)\) và điểm \(\left( {0;0} \right) \Rightarrow \left\{ \begin{array}{l}225a + 15b + c = 60\\c = 0\end{array} \right.\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{ - 4}}{{15}}\\b = 8\\c = 0\end{array} \right. \Rightarrow v\left( t \right) = - \dfrac{4}{{15}}{t^2} + 8t\)
Dựa vào đồ thị ta thấy vận đạt vận tốc cao nhất tại $t{\rm{ }} = {\rm{ }}15s$ .
Khi đó quãng đường đi được từ lúc bắt đầu đến lúc vận tốc cao nhất là: \(S = \int\limits_0^{15} {\left( { - \dfrac{4}{{15}}{t^2} + 8t} \right)dt} = 600\,\,\left( m \right)\)
Ông A có một mảnh đất hình chữ nhật \(ABCD\) có \(AB = 2\pi \,\left( m \right),\,\,AD = 5\,\left( m \right)\). Ông muốn trồng hoa trên giải đất có giới hạn bởi hai đường trung bình $MN$ và đường hình $sin$ (như hình vẽ). Biết kinh phí trồng hoa là $100.000$ đồng $/{\rm{ }}{m^2}$ . Hỏi ông A cần bao nhiêu tiền để trồng hoa trên giải đất đó?
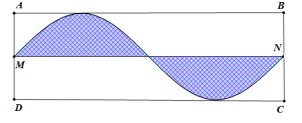
Gắn hệ trục tọa độ $Oxy$ như hình vẽ:
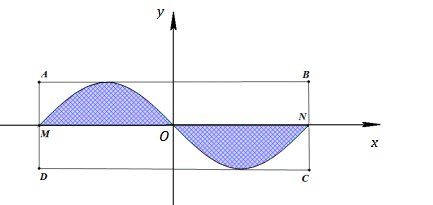
Dựa vào hình vẽ ta thấy đường $sin$ có chu kì bằng \(AB = 2\pi \) và biên độ bằng \(AM = \dfrac{1}{2}AD = \dfrac{5}{2}\) Đường hình $sin$ có phương trình \(y = - \dfrac{5}{2}\sin x\).
Đường thẳng $BC$ có phương trình \(x = \pi \).
Xét hình phẳng giới hạn bởi đồ thị hàm số \(y = - \dfrac{5}{2}\sin x\), trục $Ox$ , đường thẳng \(x = 0;\,\,x = \pi \) có $S = \int\limits_0^\pi {\left| { - \dfrac{5}{2}\sin x} \right|} dx = \dfrac{5}{2}\int\limits_0^\pi {\sin xdx} = - \left. {\dfrac{5}{2}\cos x} \right|_0^\pi = \dfrac{5}{2} + \dfrac{5}{2} = 5\,\,\left( m \right)$ .
\( \Rightarrow \) Diện tích giải đất ông A dùng để trồng hoa là \(2S = 10\,\,\left( {{m^2}} \right)\) , do đó kinh phí để trồng hoa là $1.000.000$ đồng.
Cho \(S\) là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(\left( {{C_1}} \right):\,\,y = \dfrac{2}{3}{x^3} - 3m{x^2} - 2{m^3}\) và \(\left( {{C_2}} \right):\,\,y = - \dfrac{{{x^3}}}{3} + m{x^2} - 5{m^2}x.\) Gọi $N,n$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của \(S\) khi \(m \in \left[ {1;3} \right]\). Tính \(N - n?\)
Xét phương trình hoành độ giao điểm
\(\begin{array}{l}\dfrac{2}{3}{x^3} - 3m{x^2} - 2{m^3} = - \dfrac{{{x^3}}}{3} + m{x^2} - 5{m^2}x\\ \Leftrightarrow {x^3} - 4m{x^2} + 5{m^2}x - 2{m^3} = 0\\ \Leftrightarrow \left( {x - m} \right)\left( {{x^2} - 3mx + 2{m^2}} \right) = 0\\ \Leftrightarrow {\left( {x - m} \right)^2}\left( {x - 2m} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = m\\x = 2m\end{array} \right.\end{array}\)
$m \in \left[ {1;3} \right] \Rightarrow m < 2m$ và khi \(x \in \left( {m;2m} \right) \Rightarrow x < 2m \Rightarrow {x^3} - 4m{x^2} + 5{m^2}x - 2{m^3} < 0\)
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) là:
$\begin{array}{l}S = \int\limits_m^{2m} {\left| {{x^3} - 4m{x^2} + 5{m^2}x - 2{m^3}} \right|dx} = \int\limits_m^{2m} {\left( { - {x^3} + 4m{x^2} - 5{m^2}x + 2{m^3}} \right)dx} \\ = \left. {\left( { - \dfrac{{{x^4}}}{4} + 4m\dfrac{{{x^3}}}{3} - 5{m^2}\dfrac{{{x^2}}}{2} + 2{m^3}x} \right)} \right|_m^{2m} = \dfrac{{{m^4}}}{{12}}\\m \in \left[ {1;3} \right] \Rightarrow \dfrac{1}{{12}} \le S \le \dfrac{{27}}{4} \Rightarrow \left\{ \begin{array}{l}N = \dfrac{{27}}{4}\\n = \dfrac{1}{{12}}\end{array} \right. \Rightarrow N - n = \dfrac{{20}}{3}.\end{array}$
Một tập đoàn định đầu tư vào hai dự án. Giả sử dự án đầu tư đầu có tốc độ sinh lợi nhuận là \({P_1}\left( t \right) = 50 + {t^2}\) (triệu đồng/năm), dự án thứ hai có tốc độ sinh lợi nhuận là \({P_2}\left( t \right) = 200 + 5t\) ( triệu đồng/năm). Sau t năm thì tốc độ sinh lợi nhuận của dự án hai bằng một nửa dự án một. Trong khoảng thời gian trên, chênh lệch lợi nhuận của hai dự án là bao nhiêu?
Bước 1: Tìm t
Tốc độ sinh lợi nhuận của dự án hai bằng một nửa dự án một khi
\({P_1} = 2{P_2} \Leftrightarrow 50 + {t^2} = 400 + 10t\)
\( \Leftrightarrow {t^2} - 10t - 350 = 0 \Leftrightarrow t = 5 + 5\sqrt {15} \)
Bước 2: Sử dụng tích phân để tính chênh lệch lợi nhuận thực tế
Chênh lệch lợi nhuận thực tế giữa 2 dự án trong khoảng thời gian đó là
\(\begin{array}{l}L = \int\limits_0^{5 + 5\sqrt {15} } {\left[ {{P_2}\left( t \right) - {P_1}\left( t \right)} \right]dt} \\ = \int\limits_0^{5 + 5\sqrt {15} } {\left( {350 + 10t - {t^2}} \right)} = 6674,6\end{array}\)
Một chiếc xe đua \({F_1}\) đạt tới vận tốc lớn nhất là \(360\,\,km/h\). Đồ thị bên biểu thị vận tốc \(v\) của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu là một phần của một parabol định tại gốc tọa độ \(O\), giây tiếp theo là đoạn thẳng và sau đúng ba giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trực tung biểu thị 10 m/s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó xe đã đi được quãng đường là bao nhiêu?
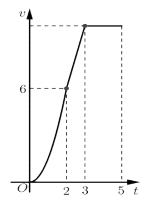
Trong 2 giây đầu, \({v_1} = a{t^2}\), lại có khi \(t = 2\,\,\left( s \right) \Rightarrow {v_1} = 60\,\,\left( {m/s} \right)\) nên \(60 = a{.2^2} \Leftrightarrow a = 15\), suy ra \({v_1} = 15{t^2}\).
Quãng đường vật đi được trong 2 giây đầu là \({s_1} = \int\limits_0^2 {{v_1}\left( t \right)dt} = \int\limits_0^2 {15{t^2}dt} = 40\,\,\left( m \right)\).
Trong giây tiếp theo, \({v_2} = mt + n\).
Ta có \(\left\{ \begin{array}{l}t = 2 \Rightarrow v = 60\\t = 3 \Rightarrow v = 360km/h = 100m/s\end{array} \right.\), nên ta có hệ phương trình \(\left\{ \begin{array}{l}2m + n = 60\\3m + n = 100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 40\\n = - 20\end{array} \right.\) \( \Rightarrow {v_2}\left( t \right) = 40t - 20\).
Quãng đường vật đi được trong giây tiếp theo là \({s_2} = \int\limits_2^3 {{v_2}\left( t \right)dt} = \int\limits_2^3 {\left( {40t - 20} \right)dt} = 80\,\,\left( m \right)\).
Trong 2 giây cuối, \({v_3} = 100\,\,\left( {m/s} \right)\).
Quãng đường vật đi được trong 2 giây cuối là \({s_3} = \int\limits_3^5 {{v_3}\left( t \right)dt} = \int\limits_3^5 {100dt} = 200\,\,\left( m \right)\).
Vậy trong 5 giây đó xe đã đi được quãng đường là: \(40 + 80 + 200 = 320\,\,\left( m \right)\).
Dòng điện xoay chiều hình sin chạy qua mạch dao động LC lí tưởng có phương trình \(i = {I_0}\sin \left( {wt + \dfrac{\pi }{2}} \right)\). Ngoài ra \(i = {q^\prime }(t)\) với \(q\) là điện tích tức thời trong tụ. Tính từ lúc \(t = 0\), điện lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian \(\dfrac{\pi }{{2w}}\) là
Tính từ lúc \(t = 0\), điện lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian \(\dfrac{\pi }{{2w}}\) là
\(q =\int_0^{\dfrac{\pi }{{2w}}}idt= \int_0^{\dfrac{\pi }{{2w}}} {{I_0}} \sin \left( {wt + \dfrac{\pi }{2}} \right)dt\)\( = - \left. {\dfrac{{{I_0}}}{w}\cos \left( {wt + \dfrac{\pi }{2}} \right)} \right|_0^{\dfrac{\pi }{{2w}}}\)
\( = - \dfrac{{{I_0}}}{w}\left[ {\cos \left( {w \cdot \dfrac{\pi }{{2w}} + \dfrac{\pi }{2}} \right) - \cos \left( {w.0 + \dfrac{\pi }{2}} \right)} \right]\)\( = - \dfrac{{{I_0}}}{w}\left[ {\cos \pi - \cos \left( {\dfrac{\pi }{2}} \right)} \right] = \dfrac{{{I_0}}}{w}\)

