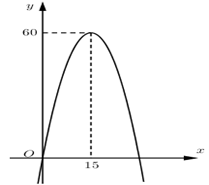
Một xe mô tô phân khối lớn sau khi chờ đèn đỏ đã bắt đầu phóng nhanh với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường Parabol (hình vẽ). Biết rằng sau $15$ giây thì xe đạt đến vận tốc cao nhất $60{\rm{ }}m/s$ và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì quãng đường xe đi được là bao nhiêu?

\(\dfrac{{250}}{3}\;{\rm{m}}\).

\(270\;{\rm{m}}\).

\(200\;{\rm{m}}\).

\(\dfrac{{110}}{3}\;{\rm{m}}\).

\(S = \dfrac{{20}}{3}\)

\(S = \dfrac{{496}}{{15}}\)

\(S = \dfrac{4}{3}\)   

\(S = \dfrac{5}{3}\)

\(\int\limits_a^b {f\left( x \right)dx}  + \int\limits_b^c {f\left( x \right)dx}  = \int\limits_a^c {f\left( x \right)dx} \)                        

\(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx}  = \int\limits_a^b {f\left( x \right)dx}  + \int\limits_a^b {g\left( x \right)dx} \)

\(\int\limits_a^b {f\left( {k.x} \right)dx}  = k\int\limits_a^b {f\left( x \right)dx} \)                         

\(\int\limits_a^b {k.f\left( x \right)dx}  = k.\int\limits_a^b {f\left( x \right)dx} \)

\(\int\limits_{}^{} {f\left( x \right)dx}  = \dfrac{{{2^x}}}{{\ln 2}} + \sin x + x + C\)

\(\int\limits_{}^{} {f\left( x \right)dx}  = \dfrac{{{2^x}}}{{\ln 2}} - \sin x + x + C\)

\(\int\limits_{}^{} {f\left( x \right)dx}  = {2^x}.\ln 2 + \sin x + x + C\)      

\(\int\limits_{}^{} {f\left( x \right)dx}  = {2^x}.\ln 2 - \sin x + x + C\)

\(S = 8\)

\(S = \dfrac{{220}}{3}\)

\(S = \dfrac{{76}}{3}\)

\(S = \dfrac{{148}}{3}\)

\(T = \dfrac{1}{2}\)

\(T = 0\)

\(T = 1\)

\(T = 2\)

\(P = 11\)

\(P = 5\)

\(P = 2\)

\(P =  - 2\)