Cho \(\Delta MNP\), em hãy chọn đáp án đúng nhất trong các đáp án sau:
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án B, C đều đúng.
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
+ Xét bộ ba: \(6cm,6cm,5cm.\) Ta có: \(6 + 6 = 12 > 5;\,\,6 + 5 = 11 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba \(6cm,6cm,5cm\) lập thành một tam giác. Loại đáp án A.
+ Xét bộ ba: \(7cm,8cm,10cm.\) Ta có: \(7 + 8 = 15 > 10;\,\,8 + 10 = 18 > 7;\,\,10 + 7 = 17 > 8\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba \(7cm,8cm,10cm\) lập thành một tam giác. Loại đáp án B.
+ Xét bộ ba: \(12cm,15cm,9cm.\) Ta có: \(12 + 15 = 27 > 9;\,\,15 + 9 = 24 > 12;\,\,9 + 12 = 21 > 15\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba \(12cm,15cm,9cm\) lập thành một tam giác. Loại đáp án C.
+ Xét bộ ba: \(11cm,20cm,9cm.\) Ta có: \(11 + 9 = 20\) (không thỏa mãn bất đẳng thức tam giác) nên bộ ba \(11cm,20cm,9cm\) không lập thành một tam giác. Chọn đáp án D.
Cho \(\Delta ABC\) có cạnh \(AB = 10cm\) và cạnh \(BC = 7cm\). Tính độ dài cạnh \(AC\) biết độ dài cạnh \(AC\) là một số nguyên tố lớn hơn \(11.\)
Gọi độ dài cạnh \(AC\) là \(x\left( {x > 0} \right)\).
Theo bất đẳng thức tam giác ta có:
\(10 - 7 < x < 10 + 7 \Rightarrow 3 < x < 17\). Vì \(x\) là số nguyên lớn hơn \(11\) nên \(x = 13.\)
Vậy độ dài cạnh \(AC = 13cm.\)
Cho tam giác \(ABC\) biết \(AB = 2\,cm;\,BC = 7\,cm\) và cạnh \(AC\) là một số tự nhiên lẻ. Chu vi tam giác \(ABC\) là:
Gọi độ dài cạnh \(AC\) là \(x\left( {x > 0} \right)\).
Theo bất đẳng thức tam giác ta có:
\(7 - 2 < x < 7 + 2 \Rightarrow 5 < x < 9\). Vì \(x\) là số tự nhiên lẻ nên \(x = 7.\) Độ dài cạnh \(AC = 7cm.\)
Chu vi tam giác \(ABC\) là: \(AB + BC + AC = 2 + 7 + 7 = 16\,(\,cm).\)
Cho tam giác \(ABC\) có \(BC = 5cm\), \(AC = \,1\,cm\) và độ dài cạnh \(AB\) là một số nguyên. Tam giác \(ABC\) là tam giác gì?
Gọi độ dài cạnh \(AB\) là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:
\(5 - 1 < x < 5 + 1 \Rightarrow 4 < x < 6\). Vì \(x\) là số nguyên nên \(x = 5.\) Độ dài cạnh \(AB = 5cm.\)
Tam giác \(ABC\) có: \(AB = BC = 5\,cm\) nên tam giác \(ABC\) cân tại \(B.\)
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng \(6cm.\) Tính cạnh \(BC\) của tam giác đó biết chu vi của tam giác là \(20cm.\)
\(\Delta ABC\) cân tại \(A.\)
- Trường hợp 1: \(AB = AC = 6cm \Rightarrow BC = 20 - 6 - 6 = 8cm.\)
Ta có: \(\left\{ \begin{array}{l}AB + AC = 6 + 6 = 12 > BC = 8cm\\AB + BC = 6 + 8 = 14 > AC = 6cm\\BC + AC = 8 + 6 = 14 > AB = 6cm\end{array} \right.\) (thỏa mãn bất đẳng thức tam giác)
- Trường hợp 2: \(BC = 6cm \Rightarrow AB = AC = \left( {20 - 6} \right):2 = 7cm.\)
Ta có: \(\left\{ \begin{array}{l}AB + AC = 7 + 7 = 14 > BC = 6cm\\AB + BC = 7 + 6 = 13 > AC = 7cm\\BC + AC = 6 + 7 = 13 > AB = 7cm\end{array} \right.\) (thỏa mãn bất đẳng thức tam giác)
Do đó \(\Delta ABC\) cân tại A có: \(AB = AC = 6cm;\,BC = 8cm\) hoặc \(BC = 6cm;\,AB = AC = 7cm\) thỏa mãn yêu cầu bài toán.
Vậy \(BC = 8\,cm\) hoặc \(BC = 6\,cm.\)
Cho \(\Delta ABC\) có \(AB < AC.\) Trên đường phân giác \(AD\) lấy điểm \(E.\) Chọn câu đúng.
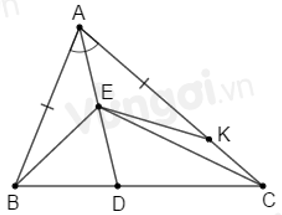
Trên cạnh \(AC\) lấy điểm \(K\) sao cho: \(AK = AB\).
Xét \(\Delta ABE\) và \(\Delta AKE\) có:
\(AB = AK\) (cách dựng)
\(\widehat {BAE} = \widehat {KAE}\) (vì \(AD\) là tia phân giác \(\widehat {BAC}\))
\(AE\) cạnh chung
\( \Rightarrow \Delta ABE = \Delta AKE\,(c.g.c)\)
\( \Rightarrow EB = EK\) (hai cạnh tương ứng).
Áp dụng bất đẳng thức tam giác vào \(\Delta CEK\) ta có: \(EC - EK < KC\) mà \(EK = EB\,\,(cmt)\) suy ra \(EC - EB < KC\) (1)
Mặt khác: \(KC = AC - AK = AC - AB\) (vì \(AK = AB\) theo cách dựng) (2)
Từ (1) và (2) suy ra: \(EC - EB < AC - AB.\)
Cho \(\Delta ABC\) có điểm \(M\) là một điểm bất kì nằm trong tam giác. So sánh \(MB + MC\) và \(AB + AC\).
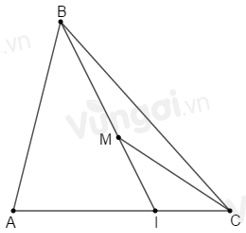
Gọi \(I\) là giao điểm của \(BM\) và \(AC\).
Áp dụng bất đẳng thức tam giác vào \(\Delta IMC\) ta có: \(MC < MI + IC\) (1)
Cộng \(MB\) vào hai vế (1) ta được: \(MC + MB < MI + IC + MB\)
\( \Rightarrow MC + MB < MI + MB + IC\)
\( \Rightarrow MC + MB < IB + IC\) (2)
Áp dụng bất đẳng thức tam giác vào \(\Delta IBA\) ta có: \(IB < IA + AB\) (3)
Cộng \(IC\) vào hai vế (3) ta được: \(IB + IC < IA + AB + IC\)
\( \Rightarrow IB + IC < IA + IC + AB\)
\( \Rightarrow IB + IC < AC + AB\) (4)
Từ (2) và (4) suy ra \(MB + MC < AB + AC\).
Có bao nhiêu tam giác có độ dài hai cạnh là \(9\,cm\) và \(3\,cm\) còn độ dài cạnh thứ ba là một số nguyên \(\left( {cm} \right)?\)
Gọi độ dài cạnh còn lại của tam giác là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:
\(9 - 3 < x < 9 + 3 \Rightarrow 6 < x < 12\). Vì \(x\) là số nguyên nên \(x \in \left\{ {7;8;9;10;11} \right\}.\)
Vì có \(5\) giá trị của \(x\) thỏa mãn nên có \(5\) tam giác thỏa mãn điều kiện đề bài.
Cho hình vẽ dưới đây với \(\widehat {xOy}\) là góc nhọn. Chọn câu đúng.
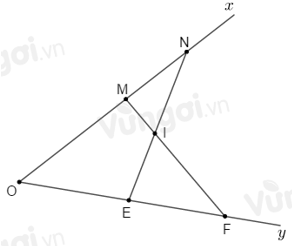
Áp dụng bất đẳng thức tam giác vào \(\Delta MIN\) ta có: \(MN < MI + NI\) (1)
Áp dụng bất đẳng thức tam giác vào \(\Delta EIF\) ta có: \(EF < IF + IE\) (2)
Cộng (1) với (2) theo vế với vế ta được:
\(MN + EF < MI + NI + IF + IE\)
\(\begin{array}{l} \Rightarrow MN + EF < \left( {MI + IF} \right) + \left( {NI + IE} \right)\\ \Rightarrow MN + EF < MF + NE\end{array}\).
Cho tam giác \(ABC\) điểm \(M\) nằm trong tam giác. Chọn câu đúng.
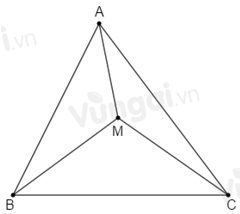
Nối các đoạn thẳng \(MA,\,MB,\,MC\).
Áp dụng bất đẳng thức tam giác vào \(\Delta AMB\) ta được: \(MA + MB > AB\) (1)
Áp dụng bất đẳng thức tam giác vào \(\Delta BMC\) ta được: \(MB + MC > BC\) (2)
Áp dụng bất đẳng thức tam giác vào \(\Delta CMA\) ta được: \(MC + MA > CA\) (3)
Cộng (1), (2) và (3) theo vế với vế ta được:
\(\begin{array}{l}MA + MB + MB + MC + MC + MA > AB + BC + CA\\ \Rightarrow 2\left( {MA + MB + MC} \right) > AB + BC + CA\\ \Rightarrow MA + MB + MC > \dfrac{{AB + BC + CA}}{2}\end{array}\).
Cho tam giác \(ABC\) điểm \(M\) nằm trong tam giác. So sánh tổng khoảng cách từ \(M\) đến ba đỉnh \(A,B,C\) với chu vi tam giác \(ABC.\)
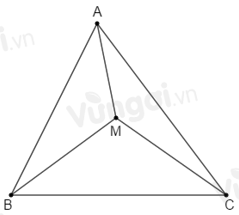
Nối các đoạn thẳng \(MA,\,MB,\,MC\).
Áp dụng bất đẳng thức tam giác vào \(\Delta AMB\) ta được: \(MA + MB > AB\) (1)
Áp dụng bất đẳng thức tam giác vào \(\Delta BMC\) ta được: \(MB + MC > BC\) (2)
Áp dụng bất đẳng thức tam giác vào \(\Delta CMA\) ta được: \(MC + MA > CA\) (3)
Cộng (1), (2) và (3) theo vế với vế ta được:
\(\begin{array}{l}MA + MB + MB + MC + MC + MA > AB + BC + CA\\ \Rightarrow 2\left( {MA + MB + MC} \right) > AB + BC + CA\\ \Rightarrow MA + MB + MC > \dfrac{{AB + BC + CA}}{2}\end{array}\).
Cho tam giác \(ABC\) điểm \(M\) nằm trong tam giác. So sánh tổng khoảng cách từ \(M\) đến ba đỉnh \(A,B,C\) với chu vi tam giác \(ABC.\)

Nối các đoạn thẳng \(MA,\,MB,\,MC\).
Áp dụng bất đẳng thức tam giác vào \(\Delta AMB\) ta được: \(MA + MB > AB\) (1)
Áp dụng bất đẳng thức tam giác vào \(\Delta BMC\) ta được: \(MB + MC > BC\) (2)
Áp dụng bất đẳng thức tam giác vào \(\Delta CMA\) ta được: \(MC + MA > CA\) (3)
Cộng (1), (2) và (3) theo vế với vế ta được:
\(\begin{array}{l}MA + MB + MB + MC + MC + MA > AB + BC + CA\\ \Rightarrow 2\left( {MA + MB + MC} \right) > AB + BC + CA\\ \Rightarrow MA + MB + MC > \dfrac{{AB + BC + CA}}{2}\end{array}\).
Cho \(\Delta ABC\), trên \(BC\) lấy điểm \(M\) bất kì nằm giữa \(B\) và \(C.\)
So sánh \(AB + AC + BC\) và \(2AM\).
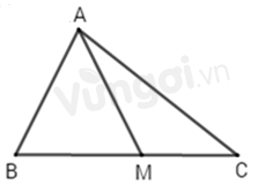
Xét \(\Delta AMB\) có: \(AM < AB + BM\) (bất đẳng thức tam giác) (1)
Xét \(\Delta AMC\) có: \(AM < AC + MC\) (bất đẳng thức tam giác) (2)
Vì M nằm giữa B và C (gt) suy ra: \(BC = BM + MC\).
Cộng (1) và (2) theo từng vế của hai bất đẳng thức ta được:
\(\begin{array}{l}AM + AM < AB + BM + AC + MC\\ \Rightarrow 2AM < AB + \left( {BM + MC} \right) + AC\\ \Rightarrow 2AM < AB + BC + AC.\end{array}\).
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án A, B, C đều đúng, đáp án D sai.
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
+ Xét bộ ba: $3cm,5cm,7cm.$ Ta có: \(\left\{ \begin{array}{l}3 + 5 = 8 > 7\\3 + 7 = 10 > 5\\5 + 7 = 12 > 3\end{array} \right.\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,7cm$ lập thành một tam giác. Loại đáp án A.
+ Xét bộ ba: $4cm,5cm,6cm$. Ta có: \(\left\{ \begin{array}{l}4 + 5 = 9 > 6\\5 + 6 = 11 > 4\\4 + 6 = 10 > 5\end{array} \right.\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $4cm,5cm,6cm$ lập thành một tam giác. Loại đáp án B.
+ Xét bộ ba: $2cm,5cm,7cm.$ Ta có: \(2 + 5 = 7\) (không thỏa mãn bất đẳng thức tam giác) nên bộ ba $2cm,5cm,7cm$ không lập thành một tam giác. Chọn đáp án C.
+ Xét bộ ba: $3cm,5cm,6cm.$ Ta có: \(\left\{ \begin{array}{l}3 + 6 = 9 > 5\\3 + 5 = 8 > 6\\5 + 6 = 11 > 3\end{array} \right.\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,6cm$ lập thành một tam giác. Loại đáp án D.
Cho \(\Delta ABC\) có cạnh $AB = 1cm$ và cạnh \(BC = 4cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số nguyên.
Gọi độ dài cạnh $AC$ là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:
\(4 - 1 < x < 4 + 1 \Leftrightarrow 3 < x < 5\). Vì $x$ là số nguyên nên $x = 4.$ Vậy độ dài cạnh $AC = 4cm.$
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 9\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
Gọi độ dài cạnh $AC$ là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:
\(9 - 1 < x < 9 + 1 \Leftrightarrow 8 < x < 10\). Vì $x$ là số nguyên nên $x = 9.$ Độ dài cạnh $AC = 9cm.$
Chu vi tam giác \(ABC\) là \(AB + BC + AC = 1 + 9 + 9 = 19\,cm.\)
Cho tam giác \(ABC\) có \(BC = 1\,cm\), \(AC = \,8\,cm\) và độ dài cạnh \(AB\) là một số nguyên \(\left( {cm} \right)\). Tam giác \(ABC\) là tam giác gì?
Gọi độ dài cạnh $AB$ là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có:
\(8 - 1 < x < 8 + 1 \Leftrightarrow 7 < x < 9.\)
Vì $x$ là số nguyên nên $x = 8.$ Độ dài cạnh $AB = 8cm.$
Tam giác \(ABC\) có \(AB = AC = 8\,cm\) nên tam giác \(ABC\) cân tại $A.$
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
Giả sử \(\Delta ABC\) cân tại $A.$
- Trường hợp 1:
\(AB = AC = 5cm \Rightarrow BC = 17 - 5 - 5 = 7cm.\)
Ta có: \(\left\{ \begin{array}{l}AB + AC = 5 + 5 = 10 > BC = 7cm\\AB + BC = 5 + 7 = 12 > AC = 5cm\\BC + AC = 7 + 5 = 12 > AB = 5cm\end{array} \right.\) (thỏa mãn bất đẳng thức tam giác)
- Trường hợp 2: \(BC = 5cm \Rightarrow AB = AC = \left( {17 - 5} \right):2 = 6cm\)
Ta có: \(\left\{ \begin{array}{l}AB + AC = 6 + 6 = 12 > BC = 5cm\\AB + BC = 5 + 6 = 11 > AC = 6cm\\BC + AC = 6 + 5 = 11 > AB = 6cm\end{array} \right.\) (thỏa mãn bất đẳng thức tam giác)
Vậy nếu \(\Delta ABC\) cân tại A có \(\left[ \begin{array}{l}AB = AC = 5cm \Rightarrow BC = 7cm\\BC = 5cm \Rightarrow AB = AC = 6cm\end{array} \right.\)
Vậy \(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)

