Câu hỏi:
2 năm trước
Cho \(\Delta ABC\), trên \(BC\) lấy điểm \(M\) bất kì nằm giữa \(B\) và \(C.\)
So sánh \(AB + AC + BC\) và \(2AM\).
Trả lời bởi giáo viên
Đáp án đúng: d
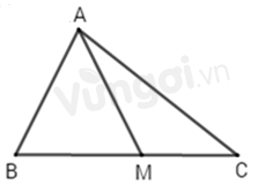
Xét \(\Delta AMB\) có: \(AM < AB + BM\) (bất đẳng thức tam giác) (1)
Xét \(\Delta AMC\) có: \(AM < AC + MC\) (bất đẳng thức tam giác) (2)
Vì M nằm giữa B và C (gt) suy ra: \(BC = BM + MC\).
Cộng (1) và (2) theo từng vế của hai bất đẳng thức ta được:
\(\begin{array}{l}AM + AM < AB + BM + AC + MC\\ \Rightarrow 2AM < AB + \left( {BM + MC} \right) + AC\\ \Rightarrow 2AM < AB + BC + AC.\end{array}\).
Hướng dẫn giải:
- Áp dụng bất đẳng thức tam giác: Trong một tam giác hiệu độ dài hai cạnh bất kì luôn nhỏ hơn độ dài cạnh còn lại.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
