Tính chất ba đường phân giác của tam giác

Điểm \(M\) cách đều hai cạnh \(AB,BC\) của tam giác \(ABC\) thì điểm \(M\) nằm trên tia phân giác của \(\widehat {ABC}\).

Tam giác \(ABC\) có hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I\) nên \(I\) là điểm cách đều ba cạnh của tam giác \(ABC.\)

Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.

Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ACB} + \widehat {ABC} = {180^0}\) (định lý tổng ba góc của một tam giác)

\( \Rightarrow \widehat {ACB} + \widehat {ABC} = {180^0} - \widehat A = {180^0} - {80^0} = {100^0}\left( 1 \right)\)

Vì \(CE\) là đường phân giác của \(\widehat {ACB}\left( {gt} \right) \Rightarrow \widehat {ECB} = \dfrac{{\widehat {ACB}}}{2}\left( 2 \right)\)

Vì \(BD\) là đường phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {CBD} = \dfrac{{\widehat {ABC}}}{2}\left( 3 \right)\)

Từ (1); (2) và (3) \( \Rightarrow \widehat {ECB} + \widehat {CBD} = \dfrac{{\widehat {ACB}}}{2} + \dfrac{{\widehat {ABC}}}{2} = \dfrac{{\widehat {ACB} + \widehat {ABC}}}{2} = \dfrac{{{{100}^0}}}{2} = {50^0}\) hay \(\widehat {ICB} + \widehat {IBC} = {50^0}\)

Xét \(\Delta BIC\) có: \(\widehat {ICB} + \widehat {IBC} + \widehat {BIC} = {180^0}\) (định lý tổng ba góc của một tam giác)

\( \Rightarrow \widehat {BIC} = {180^0} - \left( {\widehat {ICB} + \widehat {IBC}} \right) = {180^0} - {50^0} = {130^0}\).

Vì O là giao điểm của hai tia phân giác của \(\widehat {ABC}\) và \(\widehat {CAB}\) (gt)

nên CO là phân giác của \(\widehat {ACB}\) (tính chất ba đường phân giác của tam giác)

\( \Rightarrow \widehat {ACO} = \widehat {BCO}\left( 1 \right)\) (tính chất tia phân giác của một góc)

BO là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {OBA} = \widehat {OBC}\left( 2 \right)\) (tính chất tia phân giác của một góc)

Vì MN // BC (gt) \( \Rightarrow \left\{ \begin{array}{l}\widehat {MOB} = \widehat {OBC}\left( 3 \right)\\\widehat {NOC} = \widehat {OCB}\left( 4 \right)\end{array} \right.\) (so le trong )

Từ (1) và (4) \( \Rightarrow \widehat {NOC} = \widehat {ACO} \Rightarrow \Delta NOC\) cân tại N (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow NO = NC = 4cm\) (định nghĩa tam giác cân)

Từ (2) và (3) \( \Rightarrow \widehat {MOB} = \widehat {OBA} \Rightarrow \Delta MOB\) cân tại M (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow MO = BM = 3cm\) (định nghĩa tam giác cân)

\( \Rightarrow MN = MO + ON = 3 + 4 = 7cm.\)

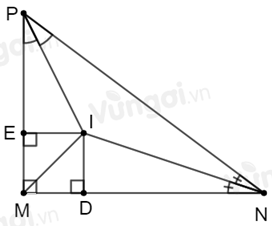
Xét \(\Delta MNP\) có các tia phân giác của \(\widehat {MNP}\) và \(\widehat {MPN}\) cắt nhau tại \(I\) nên \(I\) là giao điểm của ba đường phân giác trong \(\Delta MNP\).

Khi đó \(ID = IE\) (tính chất ba đường phân giác của tam giác) mà \(ID = 4cm\) suy ra \(IE = 4cm\).

Ta có: hai tia phân giác góc ngoài tại \(B\) và \(C\) của \(\Delta ABC\) cắt nhau tại \(N\) nên \(AN\) là tia phân giác của \(\widehat {BAC} \,(1)\)

\(\Delta ABC\) có: \(I\) cách đều ba cạnh của tam giác nên \(I\) là giao điểm của ba đường phân giác của \(\Delta ABC\).

Khi đó \(AI\) là tia phân giác của \(\widehat {BAC}\,(2)\)

Từ \((1);(2)\) suy ra: \(A,I,N\) thẳng hàng.

Do đó A đúng, B, C, D sai.

Vì \(I\) là giao của ba đường phân giác của \(\Delta ABC\) nên \(BI\) là đường phân giác của \(\Delta ABC\)

Vì \(G\) là trọng tâm \(\Delta ABC\) nên \(BG\) là đường trung tuyến của \(\Delta ABC\).

mà \(B;G;I\) thẳng hàng

Do đó \(BI\) là đường trung tuyến của \(\Delta ABC\)

Xét \(\Delta ABC\) có: \(BI\) là đường trung tuyến đồng thời là đường phân giác của \(\Delta ABC\).

Suy ra \(\Delta ABC\) cân tại \(B\).

Điểm \(E\) nằm trên tia phân giác góc \(A\) của tam giác \(ABC\) thì điểm \(E\) cách đều hai cạnh \(AB;AC.\)

Hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I\) mà ba đường phân giác của một tam giác cùng đi qua một điểm nên \(AI\) là phân giác của góc \(A.\)

+ Trọng tâm là giao điểm của ba đường trung tuyến nên đáp án A sai. Loại đáp án A.

+ Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác là đúng. Chọn đáp án B.

+ Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy sai vì tính chất này không phải đúng với mọi tam giác. Loại đáp án C.

+ Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó sai vì giao điểm của ba đường phân giác của tam giác là tâm đường tròn nội tiếp tam giác đó. Loại đáp án D.

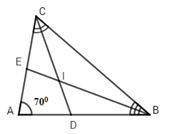
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ACB} + \widehat {ABC} = {180^0}\) (định lý tổng ba góc trong một tam giác)

\( \Rightarrow \widehat {ACB} + \widehat {ABC} = {180^0} - \widehat A = {180^0} - {70^0} = {110^0}\left( 1 \right)\)

Vì $CD$ là phân giác của \(\widehat {ACB}\left( {gt} \right) \Rightarrow \widehat {DCB} = \dfrac{{\widehat {ACB}}}{2}\left( 2 \right)\) (tính chất tia phân giác)

Vì $BE $ là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {CBE} = \dfrac{{\widehat {ABC}}}{2}\left( 3 \right)\) (tính chất tia phân giác)

Từ $(1), (2)$ và $(3)$ \( \Rightarrow \widehat {DCB} + \widehat {CBE} = \dfrac{{\widehat {ACB}}}{2} + \dfrac{{\widehat {ABC}}}{2} = \dfrac{{\widehat {ACB} + \widehat {ABC}}}{2} = {110^0}:2 = {55^0}\)  hay \(\widehat {ICB} + \widehat {IBC} = {55^0}\left( * \right)\)

Xét \(\Delta BIC\) có: \(\widehat {ICB} + \widehat {IBC} + \widehat {BIC} = {180^0}\left( {**} \right)\)( định lý tổng ba góc trong một tam giác)

Từ (*) và (**) \( \Rightarrow \widehat {BIC} = {180^0} - \left( {\widehat {ICB} + \widehat {IBC}} \right) = {180^0} - {55^0} = {125^0}\)

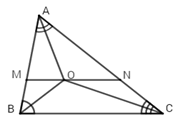
Vì O là giao điểm của hai tia phân giác của các góc \(\widehat {ABC}\) và \(\widehat {CAB}\)(gt)

Suy ra, CO là phân giác của \(\widehat {ACB}\)(tính chất 3 đường phân giác của tam giác)

\( \Rightarrow \widehat {ACO} = \widehat {BCO}\left( 1 \right)\) (tính chất tia phân giác của một góc)

BO là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {OBA} = \widehat {OBC}\left( 2 \right)\) (tính chất tia phân giác của một góc)

Vì MN // BC (gt) \(\left\{ \begin{array}{l}\widehat {MOB} = \widehat {OBC}\left( 3 \right)\\\widehat {NOC} = \widehat {OCB}\left( 4 \right)\end{array} \right.\) (so le trong)

Từ (1) và (4) \( \Rightarrow \widehat {NOC} = \widehat {NCO} \Rightarrow \Delta NOC\) cân tại N (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow NO = NC = 3cm\) (tính chất tam giác cân)

Từ (2) và (3) \( \Rightarrow \widehat {MOB} = \widehat {MBO} \Rightarrow \Delta MOB\) cân tại M (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow MB = MO = 2cm\) (tính chất tam giác cân)

\( \Rightarrow MN = MO + ON = 2 + 3 = 5cm.\)

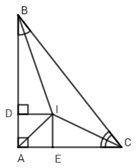
Xét \(\Delta ABC\) có các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I nên I là giao điểm của ba đường phân giác trong \(\Delta ABC\), suy ra AI là đường phân giác của \(\widehat A\) và I cách đều ba cạnh của \(\Delta ABC\)  (tính chất 3 đường phân giác của tam giác). Vậy ta loại đáp án A, B và C.

Vì I là giao điểm của ba đường phân giác trong \(\Delta ABC\) nên \( \Rightarrow DI = IE\) (tính chất 3 đường phân giác của tam giác).

$I$ là giao điểm của các đường phân giác trong tam giác nên I cách đều 3 cạnh của tam giác. Loại đáp án A.

Ta có:\(\Delta ABC\) cân tại $A,I$ là giao điểm của các đường phân giác trong tam giác nên $AI$ vừa là đường trung tuyến đồng thời là đường phân giác của \(\widehat {BAC}\)  . Mà $G$  là trọng tâm của  \(\Delta ABC\) nên $A,G,I$ thẳng hàng. Chọn B.

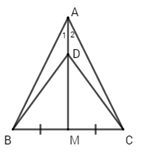
Vì \(\Delta ABC\) cân tại A (gt) và AM là trung tuyến nên AM cũng là đường phân giác của \(\widehat {BAC}\)

\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) (tính chất tia phân giác)

Xét \(\Delta ABD\) và \(\Delta ACD\) có:

\(AB = AC\left( {gt} \right)\)

\(\widehat {{A_1}} = \widehat {{A_2}}\left( {cmt} \right)\)

AD chung

\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right) \Rightarrow BD = DC\) (2 cạnh tương ứng)

\( \Rightarrow \Delta BDC\) cân tại D (dấu hiệu nhận biết tam giác cân)

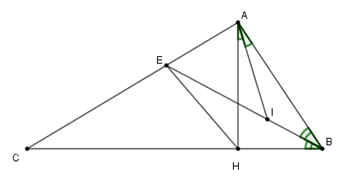
Xét tam giác \(AHB\) vuông ta có \(\widehat {BAH} + \widehat {ABH} = 90^\circ \) mà  \(\widehat {BAH} = 2\widehat C\) và \(\widehat {ABH} = 2.\widehat {IBH}\)

Suy ra \(2\widehat C + 2.\widehat {IBH} = 90^\circ  \Rightarrow 2\left( {\widehat C + \widehat {IBH}} \right) = 90^\circ \) \( \Rightarrow \widehat C + \widehat {EBH} = 45^\circ \) .

Xét tam giác \(BEC\) có \(\widehat {IEA}\) là góc ngoài tại đỉnh \(E\) nên \(\widehat {AEI} = \widehat {ECB} + \widehat {EBC} = 45^\circ \)

Xét tam giác \(AHB\) có  \(\widehat {BAH} + \widehat {HBA} = 90^\circ  \Rightarrow 2.\widehat {IAB} + 2.\widehat {IBA} = 90^\circ \)\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 90^\circ :2\)

\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 45^\circ \)

Xét tam giác \(AIB\) có \(\widehat {AIE}\) là góc ngoài tại đỉnh \(I\) nên \(\widehat {AIE} = \widehat {IAB} + \widehat {IBA} = 45^\circ \)

Xét tam giác \(IAE\) có \(\widehat {AIE} = 45^\circ  = \widehat {AEI}\)  suy ra \(\widehat {EAI} = 180^\circ  - \widehat {AEI} - \widehat {AIE} = 90^\circ \) (tổng ba góc trong tam giác)

Nên tam giác \(IAE\) vuông cân tại \(A.\)

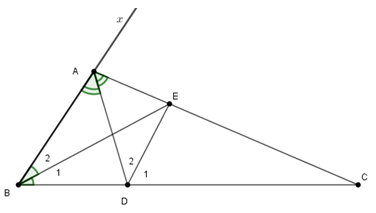
Gọi \(Ax\) là tia đối của tia \(AB.\) Ta có \(\widehat {BAD} = \widehat {DAC} = 60^\circ \) nên \(\widehat {CAx} = 60^\circ .\)

Xét \(\Delta ABD\) có \(AE\) là tia phân giác của góc ngoài đỉnh \(A,\)\(BE\) là tia phân giác của góc \(B\) và chúng cắt nhau tại \(E\) nên \(DE\) là phân giác góc ngoài của góc \(D.\)

Mà \(\widehat {EDC}\) là góc ngoài tại đỉnh \(D\) của tam giác \(BED\) nên \(\widehat {{B_1}} + \widehat {BED} = \widehat {EDC}\)

Do đó \(\widehat {BED} = \widehat {{D_1}} - \widehat {{B_1}} = \dfrac{{\widehat {ADC} - \widehat {ABC}}}{2} = \dfrac{{\widehat {BAD}}}{2} = 30^\circ \)

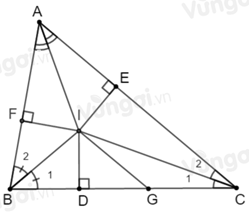
Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)

Tam giác \(ABC\) có các đường phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) cắt nhau tại \(I\) nên \(AI\) là phân giác của \(\widehat {BAC}\) (tính chất ba đường phân giác của tam giác)

Vì \(BI\) là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\) (tính chất tia phân giác)

Xét \(\Delta BFI\) vuông tại \(F\) và \(\Delta BDI\) vuông tại \(D\) có:

 \(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)

\(BI\) là cạnh chung

Do đó \(\Delta BFI = \Delta BDI\) (cạnh huyền – góc nhọn) \( \Rightarrow BF = BD\) (hai cạnh tương ứng)

Chứng minh tương tự ta có: \(AF = AE;CE = CD\).

Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\).

Xét \(\Delta BDI\) vuông tại \(D\) và \(\Delta GDI\) vuông tại \(D\) có:

\(BD = DG\) (theo cách vẽ)

\(DI\) là cạnh chung

Do đó \(\Delta BDI = \Delta GDI\) (hai cạnh góc vuông) \( \Rightarrow IB = IG\) (hai cạnh tương ứng) \( \Rightarrow \Delta IBG\) là tam giác cân tại \(I\)

\( \Rightarrow \widehat {{B_1}} = \widehat {IGB}\) (tính chất tam giác cân) \((1)\)

Ta có: \(\widehat {ABC} = 2\widehat {ACB} \Rightarrow \widehat {ACB} = \dfrac{{\widehat {ABC}}}{2} = \widehat {{B_1}}\) \((2)\)

Từ \((1)\); \((2)\) suy ra: \( \Rightarrow \widehat {IGB} = \widehat {ACB}\) mà hai góc này ở vị trí đồng vị nên \(IG//AC\) (dấu hiệu nhận biết hai đường thẳng song song)

Khi đó \(\widehat {{C_2}} = \widehat {GIC}\) (hai góc so le trong)

Mặt khác: \(\widehat {{C_2}} = \widehat {{C_1}}\) (do \(CI\) là tia phân giác của \(\widehat {ACB}\))

\( \Rightarrow \widehat {{C_1}} = \widehat {GIC} \Rightarrow \Delta GIC\) cân tại \(G\) \( \Rightarrow IG = GC\) (định nghĩa tam giác cân)

Ta có: \(AC = AE + CE\)

     \(\begin{array}{l} = AF + CD\\ = AF + DG + GC\\ = AF + BD + IG\\ = AF + BF + IB\\ = AB + IB\end{array}\)

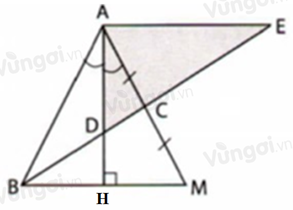
Kéo dài \(AC\) lấy điểm \(M\) sao cho: \(CM = AC\), kéo dài \(AD\) cắt \(BM\) tại \(H\)

Vì \(AD\) là phân giác của \(\widehat {BAM}\) nên \(\widehat {BAH} = \widehat {HAM} = \dfrac{{\widehat {BAM}}}{2}\) (tính chất tia phân giác)

Xét \(\Delta ABM\) có: \(BC\) là đường trung tuyến ứng với cạnh \(AM\), \(BD = 2DC\) (gt)

Do đó \(D\) là trọng tâm của \(\Delta ABM\)

Suy ra \(AD\) là đường trung tuyến của \(\Delta ABM\)

Xét \(\Delta ABM\) có: \(AD\) là đường trung tuyến đồng thời là đường phân giác

Do đó \(\Delta ABM\) cân tại \(A\) \( \Rightarrow \widehat {ABM} = \widehat {AMB}\) (tính chất tam giác cân)

Trong \(\Delta ABM\) có: \(\widehat {BAM} + \widehat {ABM} + \widehat {AMB} = {180^0}\) ( định lý tổng ba góc của tam giác)

\( \Rightarrow \widehat {BAM} + 2\widehat {ABM} = {180^0} \Rightarrow \dfrac{{\widehat {BAM}}}{2} + \widehat {ABM} = {90^0}\) hay \(\widehat {BAH} + \widehat {ABH} = {90^0}\)

Xét \(\Delta ABH\) có:

\(\widehat {BAH} + \widehat {ABH} + \widehat {AHB} = {180^0}\) (định lý tổng ba góc của tam giác)

\( \Rightarrow \widehat {AHB} = {180^0} - (\widehat {BAH} + \widehat {ABH}) = {180^0} - {90^0} = {90^0}\)

\( \Rightarrow AH \bot BM\) hay \(AD \bot BM\)

Xét \(\Delta ACE\) và \(\Delta MCB\) có:

\(AC = CM\)

\(BC = CE\,(gt)\)

\(\widehat {ACE} = \widehat {MCB}\) (hai góc đối đỉnh)

\( \Rightarrow \Delta ACE = \Delta MCB\,(c.g.c)\) \( \Rightarrow \widehat {AEC} = \widehat {MBC}\) (hai góc tương ứng)

Mà \(\widehat {AEC};\widehat {MBC}\) ở vị trí so le trong

\( \Rightarrow AE//BM\) (dấu hiệu nhận biết hai đường thẳng song song)

Mà \(AD \bot BM \Rightarrow AD \bot AE\) (quan hệ giữa tính vuông góc với tính song song)

Do đó \(\Delta ADE\) vuông tại \(A\).