Chọn câu đúng. Cho tam giác ABC vuông tại B thì theo định lý Pytago ta có:
Áp dụng định lí Py-ta-go cho tam giác ABC vuông tại B ta có: AC2=AB2+BC2.
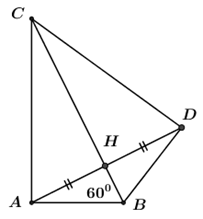
Tính số đo của góc BDC.

+ Ta có AH vuông góc với BC tại H và điểm D thuộc tia đối của tia HA nên tam giác AHC vuông tại A, tam giác DHC vuông tại H.
Xét hai tam giác vuông AHC và DHC ta có:
AH=HD (gt)
HC là cạnh chung
Vậy ΔAHC=ΔDHC (hai cạnh góc vuông)
+) Ta có ΔAHC=ΔDHC⇒^ACH=^DCH=30o(2 góc tương ứng) và AC=DC (2 cạnh tương ứng)
Xét hai tam giác ABC và DBC ta có:
BC là cạnh chung
^ACB=^DCB=30o
AC=CD
Vậy ΔABC=ΔDBC(c.g.c)⇒^BAC=^BDC=90o(2 góc tương ứng)
Vậy ^BDC=90o
So sánh AB và AC, BH và HC
+) Tam giác ABC vuông tại A nên ta có:
ˆB+ˆC=90o⇒ˆC=90o−ˆB=90o−60o=30o
Trong tam giác ABC ta có ˆB>ˆC suy ra AC>AB.
Xét tam giác ABC vuông tại A có:
BH là hình chiếu của AB trên BC; HC là hình chiếu của AC trên BC
Mà AB<AC (cmt)
Suy ra BH<HC.
So sánh AB và AC, BH và HC

+) Tam giác ABC vuông tại A nên ta có:
ˆB+ˆC=90o⇒ˆC=90o−ˆB=90o−60o=30o
Trong tam giác ABC ta có ˆB>ˆC suy ra AC>AB.
Xét tam giác ABC vuông tại A có:
BH là hình chiếu của AB trên BC; HC là hình chiếu của AC trên BC
Mà AB<AC (cmt)
Suy ra BH<HC.
Chọn câu đúng.

+ Đặt BC=a,CA=b,AB=c . Ta có:
AE=AC−−CE=AC−−CDAF=AB−−BF=AB−−BD
Suy ra AE+AF=AC−−CD+AB−−BD=AB+AC−−(BD+CD)
Hay 2.AE=AB+AC−−BC=c+b−−a.
Do đó AE=c+b−a2
Ta có EA1=EA+AA1=EA+BC=c+b−a2+a=c+b+a2
Chứng minh tương tự ta có: FB1=c+b+a2;DC1=c+b+a2
Vậy EA1=FB1=DC1.
Chọn câu đúng.
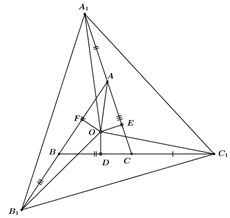
+ Do OD,OE,OF lần lượt vuông góc với BC,AC,AB nên các tam giác AOE,AOF,BOF,BOD,COE,COD là các tam giác vuông.
O là giao điểm các đường phân giác nên suy ra OD=OE=OF.
Xét hai tam giác vuông AOE và AOF ta có:
AO là cạnh chung;
OE=OF
Vậy ΔAOE=ΔAOF(cạnh huyền – cạnh góc vuông)
Suy ra AE=AF (2 cạnh tương ứng)
Chứng minh tương tự ta có: BD=BF,CD=CE.
Chọn câu đúng.

+ Do OD,OE,OF lần lượt vuông góc với BC,AC,AB nên các tam giác AOE,AOF,BOF,BOD,COE,COD là các tam giác vuông.
O là giao điểm các đường phân giác nên suy ra OD=OE=OF.
Xét hai tam giác vuông AOE và AOF ta có:
AO là cạnh chung;
OE=OF
Vậy ΔAOE=ΔAOF(cạnh huyền – cạnh góc vuông)
Suy ra AE=AF (2 cạnh tương ứng)
Chứng minh tương tự ta có: BD=BF,CD=CE.
Chọn đáp án đúng nhất. Tam giác ABC có ˆB=ˆC=60o thì tam giác ABC là tam giác:
Áp dụng định lí tổng ba góc trong tam giác ta có: ˆA+ˆB+ˆC=180o
⇒ˆA=180o−ˆB−ˆC=180o−60o−60o=60o
Tam giác ABC có ˆA=ˆB=ˆC=60o nên tam giác ABC là tam giác đều.
Tam giác cân có góc ở đỉnh là 80o. Số đo góc ở đáy là:
Giả sử tam giác ABC cân tại A có ˆA=80o. Ta sẽ tìm số đo góc B hoặc góc C.
Áp dụng định lí tổng ba góc trong tam giác ta có: ˆA+ˆB+ˆC=180o
⇒ˆB+ˆC=180o−ˆA=180o−80o=100o
Do tam giác ABC cân tại A nên ˆB=ˆC. Từ đó suy ra ˆB=ˆC=ˆB+ˆC2=100o2=50o
Vậy số đo góc ở đáy là 50o.
Cho tam giác ABC có ˆB=80o;ˆC=30o, khi đó ta có:
Áp dụng định lí tổng ba góc trong tam giác ta có: ˆA+ˆB+ˆC=180o
⇒ˆA=180o−ˆB−ˆC=180o−80o−30o=70o
Tam giác ABC có ˆB>ˆA>ˆC nên áp dụng quan hệ giữa cạnh và góc trong tam giác ta suy ra AC>BC>AB
Chọn đáp án đúng. Cho tam giác ABC có đường cao AH . Biết B nằm giữa H và C. Ta có:
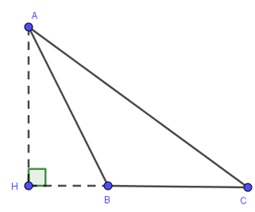
Vì ^ABC là góc ngoài tại đỉnh B của tam giác AHB nên ^ABC=^AHB+^BAH⇒^ABC>^AHB
Hay ˆB>90∘ nên ^ABC là góc tù và là góc lớn nhất trong tam giác ABC⇒AC>AB;AC>BC
Cho tam giác ABC có AB=15cm,BC=8cm. Tính độ dài cạnh AC biết độ dài này (theo đơn vị cm) là một số nguyên tố lớn hơn bình phương của 4.
Theo bất đẳng thức tam giác ta có: AB−BC<AC<AB+BC
⇒15−8<AC<15+8 hay 7<AC<23
Theo đề bài ta có AC là số nguyên tố và AC>42=16
⇒AC=17cm hoặc AC=19cm
+) Nếu AC=17cm thì 15+8>17 (thỏa mãn bất đẳng thức tam giác)
+) Nếu AC=19cm thì 15+8>19 (thỏa mãn bất đẳng thức tam giác)
Vậy độ dài cạnh AC có thể là 17cm hoặc 19cm
Cho tam giác MON, trung tuyến MI, biết MI=12ON và I∈ON. Khẳng định nào sau đây đúng?

Vì MI=ON2⇒MI=IO=IN
Xét tam giác MIO có MI=IO nên tam giác MIO cân tại I⇒^M1=ˆO (tính chất tam giác cân)
Xét tam giác MIN có MI=IN nên tam giác MIN cân tại I⇒^M2=ˆN (tính chất tam giác cân)
Suy ra ^M1+^M2=ˆO+ˆN⇔^OMN=ˆO+ˆN
Xét tam giác MON có ^OMN+ˆN+ˆO=180∘ (định lý tổng ba góc trong tam giác)
Suy ra ^OMN=ˆO+ˆN=180∘2=90∘ nên tam giác MON vuông tại M.
Cho hình vẽ. Biết ^IHK=60∘ Tính ^KHO.
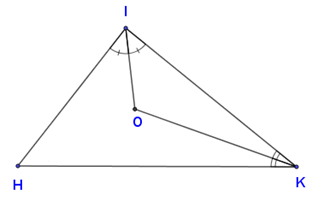
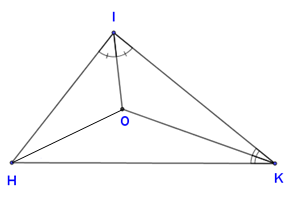
Ta có:^HIO=^KIO(gt)⇒IO là tia phân giác góc KIH (1)
Lại có ^IKO=^HKO(gt)⇒KO là tia phân giác góc IKH (2)
Từ (1) và (2) suy ra O là giao điểm hai tia phân giác
Do đó O thuộc tia phân giác góc H (tính chất ba đường phân giác trong tam giác)
Suy ra ^IHO=^KHO=^IHK2=60∘2=30∘ (tính chất đường phân giác)
Cho tam giác vuông MNP như hình vẽ. Trực tâm tam giác MNP là

Ta thấy MN⊥NP nên MN;NP là các đường cao của tam giác MNP mà hai đường này giao nhau tại N nên N là trực tâm tam giác MNP.
Cho tam giác ABC, biết số đo các góc tỉ lệ với nhau theo tỉ số: ˆA:ˆB:ˆC=2:3:4. Hãy so sánh ba cạnh của tam giác ABC.

Theo bài ra ta có ˆA:ˆB:ˆC=2:3:4⇒ˆC>ˆB>ˆA
Suy ra AB>AC>BC (quan hệ giữa góc và cạnh đối diện trong ΔABC )
Cho tam giác ABC vuông tại A có AB=5cm,AC=12cm. Gọi G là trọng tâm tam giác ABC, khi đó GA+GB+GC bằng: (làm tròn đến 2 chữ số sau dấu phẩy)
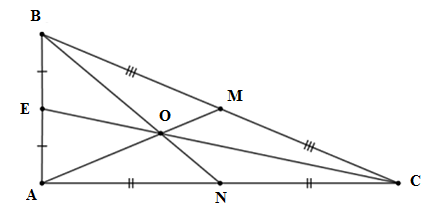
Gọi AM,BN,CE là ba đường trung tuyến của tam giác ABC.
ΔABC vuông tại A nên theo định lí Py-ta-go ta có:
BC2=AB2+AC2⇒BC2=52+122=169⇒BC=13cm
Ta có AM,BN,CE là các đường trung tuyến ứng với các cạnh BC,AC,AB của tam giác vuông ABC
Suy ra M,N,E lần lượt là trung điểm của các cạnh BC,AC,AB.
⇒AN=12AC=12⋅12=6cm;AE=12AB=12⋅5=2,5cm
Áp dụng định lí Py-ta-go với tam giác ABN vuông tại A ta có:
AB2+AN2=BN2⇒52+62=BN2⇒BN2=61⇒BN=√61cm
Áp dụng định lí Py-ta-go với tam giác AEC vuông tại A ta có:
AE2+AC2=CE2⇒2,52+122=CE2⇒CE2=6014⇒CE=√6012cm
Ta có tam giác ABC vuông tại A,AM là đường trung tuyến ứng với cạnh huyền BC nên ta có:
⇒AM=12BC=12⋅13=132cm
Ta có : GA+GB+GC=23AM+23BN+23CE=23(AM+BN+CE) (do G là trọng tâm tam giác ABC )
⇒GA+GB+GC=23(132+√61+√6012)≈17,71cm
Cho ΔABC vuông tại A có AB=4cm,BC=5cm. So sánh các góc của tam giác ABC.
Vì tam giác ABC vuông tại A nên theo định lý Pytago ta có AB2+AC2=BC2⇔AC2=BC2−AB2=52−42=9=32 ⇒AC=3cm
Từ đó ta có AC<AB<BC(3cm<4cm<5cm) suy ra ˆB<ˆC<ˆA (định lý về góc và cạnh đối diện trong tam giác)
Cho tam giác MNP cân ở M, trung tuyến MA, trọng tâm G. Biết MN=13cm,NA=12cm. Khi đó độ dài MG là:
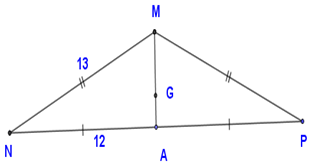
Vì ΔMNP cân tại M có MA là trung tuyến nên MA cũng là đường cao (tính chất các đường trong tam giác cân)
Xét ΔMAN vuông tại A, theo định lý Pytago ta có: MA2+NA2=MN2⇔MA2=MN2−NA2=132−122=25⇒MA=5cm
Vì MA là trung tuyến, G là trọng tâm nên theo tính chất trọng tâm tam giác ta có MG=23MA=23.5=103cm
Cho ΔMNP có ˆM=400, các đường phân giác NH và PK của ˆN và ˆP cắt nhau tại I. Khi đó ^NIP bằng:
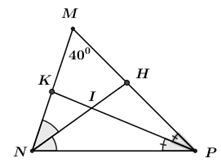
Xét ΔMNP có: ˆM+^MNP+^MPN=1800 (định lý tổng ba góc trong một tam giác)
⇒^MNP+^MPN=1800−ˆM=1800−400=1400(1)
Vì NH là phân giác của ^MNP(gt)⇒^HNP=^MNP2(2) (tính chất tia phân giác)
Vì PK là phân giác của ^MNP(gt)⇒^NPK=^MPN2(3) (tính chất tia phân giác)
Từ (1) (2) và (3) ⇒^INP+^IPN=^MNP2+^MPN2=^MNP+^MPN2=1400:2=700 hay ^INP+^IPN=700(∗)
Xét ΔINP có: ^INP+^IPN+^NIP=1800(∗∗)( định lý tổng ba góc trong một tam giác)
Từ (*) và (**) ⇒^NIP=1800−(^INP+^IPN)=1800−700=1100

