Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: $a$, $2a$, $\dfrac{a}{2}$ thể tích của hình hộp chữ nhật đó là:
Thể tích của hình hộp chữ nhật là \(V = a.2a.\dfrac{a}{2} = {a^3}\) (đvtt)
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ , chọn khẳng định đúng.
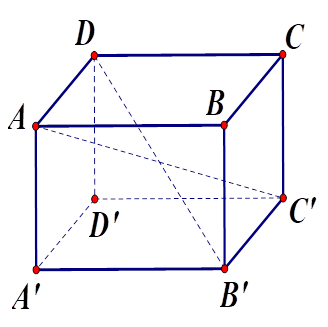
Ta có $AC'$ cắt $DB'$ vì $AD$ // $B'C'$ , $AD = B'C'$ nên $ADC'B'$ là hình bình hành, do đó $AC'$ cắt $DB'$ nên A đúng.
$AC'$ không cắt $BC$ vì chúng không có điểm chung nên B sai.
$AB$ và $CD$ song song nên chúng không cắt nhau nên D sai.
$AC$ và $BD$ cắt nhau nên C sai.
Hãy chọn câu đúng. Cạnh của một hình lập phương bằng $5\,cm$ khi đó thể tích của nó là:
Thể tích hình lập phương cạnh \(5\,cm^3\) là:
\(V = {5^3} = 125\;c{m^3}\)
Các kích thước của hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) là $DC = 6cm$ , $CB = 3cm$ . Hỏi độ dài của \(A'B'\) và $AD$ là bao nhiêu $cm$ ?
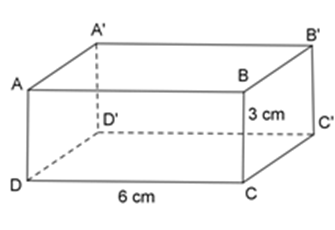
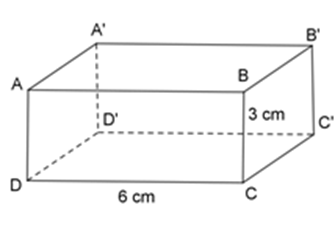
Vì \(ABC{\rm{D}}.A'B'C'D'\) là hình hộp chữ nhật nên $ABCD,$ \(ABB'A'\) là hình chữ nhật.
Xét hình chữ nhật $ABCD$ có: $AD = BC = 3cm,DC = AB = 6cm$
Xét hình chữ nhật \(ABB'A'\) có: \(A'B' = AB = 6\;cm\)
Vậy \(A'B'\) và $AD$ lần lượt dài $6 cm$ và $3 cm.$
Một bể nước dạng hình hộp chữ nhật có kích thước các số đo trong lòng bể là: dài $4$ m, rộng $3$ m, cao $2,5$ m. Biết \(\dfrac{3}{4}\) bể đang chứa nước. Hỏi thể tích phần bể không chứa nước là bao nhiêu?
Vì bể nước có dạng hình hộp chữ nhật nên ta tính được thể tích bể nước là: \(V = 4.3.2,5 = 30\;{m^3}\)
Vì \(\dfrac{3}{4}\)bể đang chứa nước nên thể tích phần bể chứa nước là: Vchứa nước\( = \dfrac{3}{4}V = \dfrac{3}{4}30 = 22,5\;{m^3}\)
Vậy thể tích phần bể không chứa nước là: Vkhông chứa nước = V \( - \) Vchứa nước\( = 30 - 22,5 = 7,5\;{m^3}\)
Hình lập phương $A$ có cạnh bằng \(\dfrac{2}{3}\) cạnh hình lập phương $B$ . Hỏi thể tích hình lập phương $A$ bằng bao nhiêu phần thể tích hình lập phương $B$ .
Gọi chiều dài một cạnh của hình lập phương $A$ là $a$ .
Vì hình lập phương $A$ có cạnh bằng \(\dfrac{2}{3}\) cạnh của hình lập phương $B$ nên chiều dài $1$ cạnh của hình lập phương $B$ là \(\dfrac{3}{2}a\).
Thể tích hình lập phương A là: \({V_A} = {a^3}\)
Thể tích hình lập phương B là: \({V_B} = {\left( {\dfrac{3}{2}a} \right)^3} = \dfrac{{27}}{8}{a^3}\)
\( \Rightarrow {V_B} = \dfrac{{27}}{8}{V_A} \Rightarrow {V_A} = \dfrac{8}{{27}}{V_B}\)
Vậy thể tích hình lập phương $A$ bằng $\dfrac{8}{{27}}$ thể tích hình lập phương $B$ .
Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài $80c$ m, chiều rộng $50$ cm. Mực nước trong bể cao $35$ cm. Người ta cho vào bể một hòn đá thì thể tích tăng $20000\,\,c{m^3}$ . Hỏi mực nước trong bể lúc này cao bao nhiêu?
Thể tích phần bể chứa nước ban đầu là:
$V = 80.50.35 = 140000\;c{m^3}$
Sau khi cho vào một hòn đá thể tích tăng $20000$ $cm^3$. Vậy thể tích phần bể chứa nước lúc sau là:
${V_1} = V + 20000 = 140000 + 20000 = 160000\;c{m^3}$
Vì chiều dài và chiều rộng bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi.
Gọi chiều cao mực nước lúc sau là $h$ cm. Ta có:
$V = 80.50.h = 160000 $$\Rightarrow h = \dfrac{V}{{80.50}} = \dfrac{{160000}}{{80.50}} = 40\;cm$
Một người thuê sơn mặt trong và mặt ngoài của $1$ cái thùng sắt không nắp dạng hình lập phương có cạnh $0,8$ m. Biết giá tiền mỗi mét vuông là $15000$ đồng. Hỏi người ấy phải trả bao nhiêu tiền?
Thùng sắt (không nắp) có dạng hình lập phương \( \Rightarrow \)Thùng sắt có 5 mặt bằng nhau.
Diện tích một mặt thùng sắt là:
\(S = 0,{8^2} = 0,64\;{m^2}\)
Ta có diện tích mặt trong thùng sắt bằng diện tích mặt ngoài thùng sắt. Vậy diện tích mặt trong và mặt ngoài thùng sắt là:
\({S_{mt}} = {S_{mn}} = 5S = 5.0,64 = 3,2\;{m^2}\)
Số tiền người thuê sơn thùng sắt cần trả là:
\(({S_{mt}} + {S_{mn}}).15000 = (3,2 + 3,2).15000 = 6,4.15000 = 96000\) đồng.
Hãy kể tên các mặt của hình hộp chữ nhật $ABCD.A'B'C'D'$. Hãy chọn câu sai
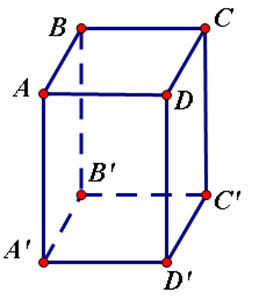
Hình hộp chữ nhật gồm $6$ mặt:
\(\left( {ADD'A'} \right);\,\left( {DCC'D'} \right);\left( {BCC'B'} \right);\,\left( {ABB'A'} \right);\,\left( {ABCD} \right);\left( {A'B'C'D'} \right)\)
Hãy chọn câu sai. Hình hộp chữ nhật $ABCD.{\rm{ }}A'B'C'D'$ có
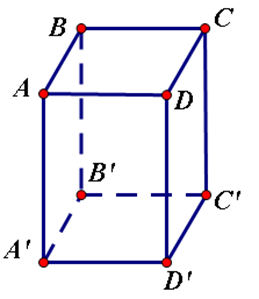
Hình hộp chữ nhật có \(12\) cạnh:
\(\begin{array}{l}AB;BC;CD;DA;A'B';C'D';\\B'C';D'A';AA';BB';CC';DD'\end{array}\)
Nên C sai.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Gọi tên mặt phẳng chứa đường thẳng $A'B$ và $CD'$. Hãy chọn câu đúng.
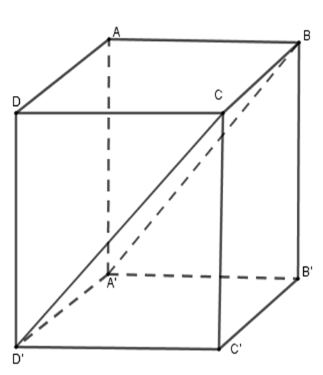
Mặt phẳng chứa đường thẳng \(A'B\) và \(CD'\) là mặt phẳng đi qua bốn điểm \(A',\,B,\,C,\,D'\) hay chính là $mp \left( {A'BCD'} \right).$
Hãy kể tên những cạnh bằng nhau của hình hộp chữ nhật $ABCD.A'B'C'D'$.
Hãy chọn câu sai
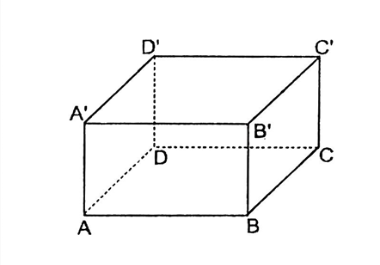
Các cạnh bằng nhau của hình hộp chữ nhật \(AA' = BB' = CC' = DD'\) ; \(AB = DC = A'B' = D'C'\) ;
\(AA' = BB' = CC' = DD'\) .
Nên D sai.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Có bao nhiêu cạnh cắt cạnh $AB$
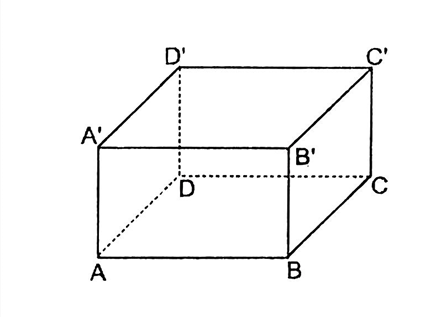
Có bốn cạnh cắt $AB$ là $AD,AA',BC,BB'.$
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Có bao nhiêu cạnh song song với cạnh $AB$
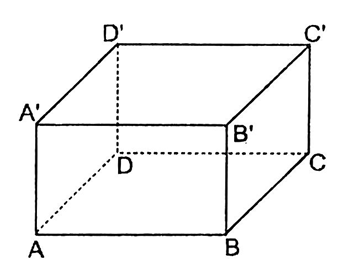
Có ba cạnh song song với $AB$ là $A'B',CD,C'D'$ .
Trong các mặt của một hình hộp chữ nhật, tính số cặp mặt song song với nhau là
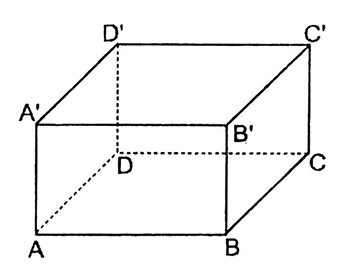
Có $3$ cặp mặt phẳng song song là mp \(\left( {ABB'A'} \right)\) và mp \(\left( {DCC'D'} \right)\) ; mp \(\left( {ABCD} \right)\) và mp \(\left( {A'B'C'D'} \right)\); mp \(\left( {ADD'A'} \right)\) và mp \(\left( {BCC'B'} \right)\)
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Gọi $M,{\rm{ }}N,{\rm{ }}I,{\rm{ }}K$ theo thứ tự là trung điểm $AA',{\rm{ }}BB',{\rm{ }}CC',{\rm{ }}DD'$. Hãy chọn câu sai
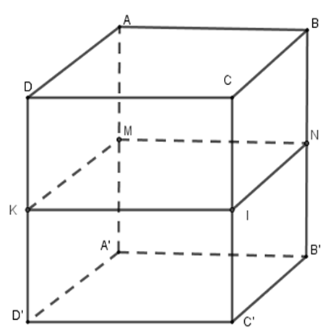
Vì $M,{\rm{ }}N,{\rm{ }}I,{\rm{ }}K$ theo thứ tự là trung điểm $AA',{\rm{ }}BB',{\rm{ }}CC',{\rm{ }}DD'$ nên \(KM = IN;\,KM{\rm{//}}IN\)
Suy ra bốn điểm $M,{\rm{ }}N,{\rm{ }}I,{\rm{ }}K$ cùng thuộc một mặt phẳng.
Lại có \(KM{\rm{//}}AD{\rm{//}}A'D'\) nên mp $\left( {MNIK} \right)$// mp $\left( {ABCD} \right)$ và mp $\left( {MNIK} \right)$// mp $\left( {A'B'C'D'} \right)$
Ta thấy mp \(\left( {MNIK} \right)\) và mp \(\left( {ABB'A'} \right)\) cắt nhau theo đường thẳng \(MN\) nên chúng không song song.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $O$ và $O'$ lần lượt là tâm \(ABCD;\,A'B'C'D'\) . Hai mp $(ACC'A')$ và mp $\left( {BDD'B'} \right)$ cắt nhau theo đường nào?
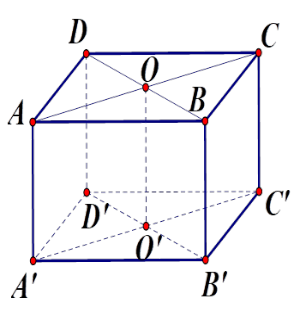
Gọi $O$ là giao điểm của $AC$ và $BD$ . Ta có \(O \in AC\) nên \(O \in {\rm{mp}}\left( {ACC'A'} \right)\), \(O \in BD\) nên \(O \in {\rm{mp}}\left( {BDD'B'} \right)\), do đó $O$ thuộc cả hai mặt phẳng trên. (1)
Gọi \(O'\) là giao điểm của \(A'C'\) và \(B'D'\) .
Chứng minh tương tự, \(O'\) thuộc cả hai mặt phẳng trên. (2)
Từ (1) và (2) suy ra hai mặt phẳng $(ACC'A')$ và mp $\left( {BDD'B'} \right)$ cắt nhau theo đường thẳng \(OO'\) .
Cho hình lập phương $ABCD.A'B'C'D'$. Tính số đo góc \(AB'C\) .
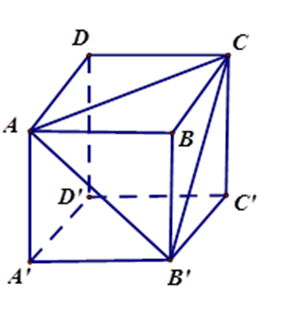
Các tam giác $ABC,ABB',CBB'$ vuông cân nên $AC = AB' = B'C$ .
Tam giác $AB'C$ có ba cạnh bằng nhau nên là tam giác đều, suy ra \(\widehat {AB'C} = {60^0}\) .
Tình độ dài của một chiếc hộp hình lập phương, biết rằng nếu độ dài mỗi cạnh của hộp tang thêm $2\,cm$ thì diện tích phải sơn $6$ mặt bên ngoài của hộp đó tăng thêm $216\,c{m^2}$ .
Diện tích phải sơn một mặt của hình hộp tăng thêm \(216:6 = 36\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Gọi độ dài cạnh của hình lập phương là $x\,\left( {cm} \right)$ , \(x > 0\)
Phương trình \({\left( {x + 2} \right)^2} - {x^2} = 36\)
\( \Leftrightarrow {x^2} + 4x + 4 - {x^2} = 36\)
\(\Leftrightarrow 4x = 32\)
\(\Leftrightarrow x = 8\) (TM )
Độ dài cạnh của chiếc hộp bằng $8cm$ .

