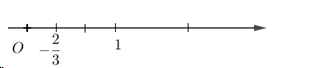
Tập hợp số hữu tỉ được kí hiệu là
Tập hợp các số hữu tỉ được kí hiệu là Q.
Tập hợp các số tự nhiên kí hiệu là N.
Tập hợp số tự nhiên khác 0 kí hiệu là N∗
Chọn câu đúng
Ta có −6∈Z;−6∉N nên D sai.
23∈Q;23∉Z nên B sai.
−92∈Q nên C sai
32∈Q nên A đúng.
Số nào dưới đây là số hữu tỉ dương?
−2−3=23>0;−25<0;−515<0;2−15<0.
Vậy số hữu tỉ dương là −2−3.
Số hữu tỉ là số được viết dưới dạng phân số ab với:
Số hữu tỉ là số được viết dưới dạng phân số ab trong đó a,b∈Z;b≠0.
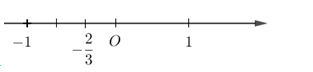
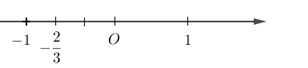
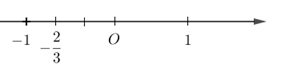
Số −23 được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
Biểu diễn số −23 trên trục số ta được:
Trong các phân số sau, phân số nào không bằng phân số 34?
69=23;912=34;−6−8=34;−3−4=34.
Vậy phân số không bằng phân số 34 là 69.
Cho các câu sau:
(I) Số hữu tỉ dương lớn hơn số hữu tỉ âm
(II) Số hữu tỉ dương lớn hơn số tự nhiên
(III) Số 0 là số hữu tỉ âm
(IV) Số nguyên dương là số hữu tỉ.
Số các câu đúng trong các câu trên là
(I) đúng
(II) sai vì số hữu tỉ dương chưa chắc lớn hơn số tự nhiên. Ví dụ: 54<2 .
(III) sai vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm
(IV) đúng vì mọi số nguyên dương đều là số hữu tỉ với mẫu số là 1.
Vậy có hai câu đúng.
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: −1217;−317;−1617;−117;−1117;−1417;−917.
Vì −1>−3>−9>−11>−12>−14>−16
Nên ta có −117>−317>−917>−1117>−1217>−1417>−1617
Số hữu tỉ lớn nhất trong các số 78;23;34;1819;2728 là:
Phần bù với 1 của các số 78;23;34;1819;2728 lần lượt là 18;13;14;119;128
Mà 28>19>8>4>3 nên 128<119<18<14<13
Suy ra 2728>1819>78>34>23
Số hữu tỉ lớn nhất là: 2728
So sánh hai số x=2−5 và y=−313
Ta có x=2−5=2.(−13)(−5).(−13)=−2665 và y=−313=−3.513.5=−1565
Mà −26<−15⇒−2665<−1565 hay x<y .
So sánh x=20022003 và y=1413
Ta có x=20022003<20032003=1 hay x<1
Và y=1413>1313=1 hay y>1
Từ đó suy ra y>1>x hay y>x .
Biểu diễn các số: 14; 0,25; −25−100; 520 bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
0,25=25100=14;−25−100=14;520=14.
Nên 14=0,25=−25−100=520
Do đó các số 14;0,25;−25−100;520 được biểu diễn cùng một điểm trên trục số.
Trong các phân số 1418;2426;26−28;−2830;7278 có bao nhiêu phân số bằng phân số 1213 ?
1418=79;2426=1213;7278=1213.
Ta có 26−28<0<1213;−2830<0<1213 ; 79=91117<108117=1213
Vậy có 2 phân số bằng phân số 1213 là: 2426;7278.
Cho số hữu tỉ x=a−32. Với giá trị nào của a thì x là số nguyên dương;
Để x=a−32 là số nguyên dương thì (a−3)>0 và (a−3)⋮2
Giả sử a−3=2k(k∈N∗) suy ra a=3+2k(k∈N∗)
Cho số hữu tỉ y=2a−1−3. Với giá trị nào của a thì y không là số dương và cũng không là số âm.
Vì số hữu tỉ 0 không là số dương cũng không là số âm nên để y=2a−1−3 không dương cũng không âm thì
y=0 suy ra 2a−1−3=0 ⇒2a−1=0⇒a=12 .