Chọn câu trả lời đúng trong các câu sau: Trong mặt phẳng,
Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.
Chọn câu đúng.
Tiên đề Ơ-clit: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song song với đường thẳng đó.”
Trong số các câu sau có bao nhiêu câu đúng?
Nếu một đường thẳng cắt hai đường thẳng song song thì:
(I) Hai góc đồng vị bằng nhau;
(II) Hai góc so le ngoài bằng nhau;
(III) Hai góc trong cùng phía bù nhau;
(IV) Hai góc so le trong bằng nhau.
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
+ Hai góc so le trong còn lại bằng nhau, hai góc so le ngoài bằng nhau.
+ Hai góc đồng vị bằng nhau
+ Hai góc trong cùng phía bù nhau
Nên cả (I), (II), (III), (IV) đều đúng.
Cho hình vẽ dưới đây :
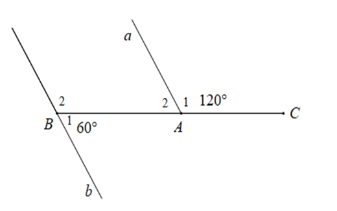
Chọn câu sai.
Vì \(\widehat {{A_1}};\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) \( \Rightarrow 120^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 60^\circ \)
Tương tự vì \(\widehat {{B_1}};\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) \( \Rightarrow 60^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 120^\circ \)
Nhận thấy \(\widehat {{A_2}} = \widehat {{B_2}} = 120^\circ \) mà hai góc ở vị trí đồng vị nên \(a//b.\)
Vậy A sai.
Cho hình vẽ:
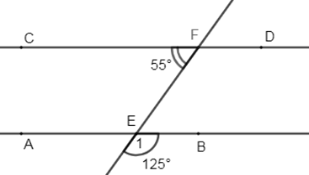
Biết \(\widehat {CF{\rm{E}}} = {55^0},\,\widehat {{E_1}} = {125^0}\) . Khi đó:
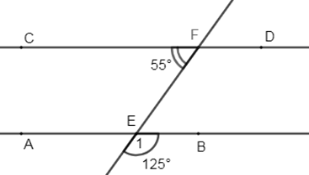
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù (gt)
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \)\(\Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} \)\(= {180^0} - {125^0} = {55^0} \)\(\Rightarrow \widehat {BEF} = \widehat {CFE} = {55^0}\)
Mà \(\widehat {BEF}\) và \(\widehat {CFE}\) là hai góc so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song)
Lại có \(\widehat {{E_1}}=\widehat {{AEF}}\) (hai góc đối đỉnh) nên \(\widehat {{AEF}}=125^0\)
Vậy cả A, B đều đúng.
Cho hình vẽ sau, biết \(x//y\) và \(\widehat {{M_1}} = {55^0}\). Tính \(\widehat {{N_1}}\).
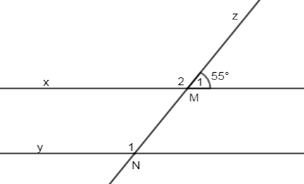
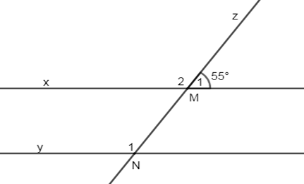
Ta có: \(\widehat {{M_1}} + \widehat {{M_2}} = {180^0} \Rightarrow \widehat {{M_2}} = {180^0} - {55^0} = {125^0}\) (kề bù)
Vì \(x//y\left( {gt} \right) \Rightarrow \widehat {{M_2}} = \widehat {{N_1}} = {125^0}\) (2 góc đồng vị)
Cho hình vẽ sau, biết \(a//b\) và \(\widehat {{A_1}} = {100^0}\). Tính $\widehat {{B_1}},\widehat {{B_2}}$.
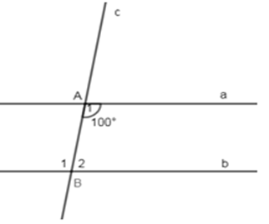
Vì \(a//b\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\, = {100^0}\) (hai góc so le trong)
Lại có: \(\widehat {{A_1}} + \widehat {{B_2}} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {{B_2}} = {180^0} - \widehat {{B_1}} = {180^0} - {100^0} = {80^0}.\)
Cho hình vẽ sau:
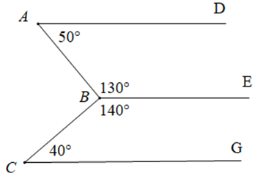
Chọn câu đúng.
Vì \(\widehat A + \widehat {ABE} = 50^\circ + 130^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên $AD//BE.$
Vì \(\widehat {CBE} + \widehat C = 140^\circ + 40^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên \(BE//CG.\)
Vậy cả A, B đều đúng.
Cho hình 21 biết \(a \bot c\) và \(b \bot c\), đồng thời \(2\widehat {{C_4}} = 3\widehat {{D_5}}.\) Tìm số đo \(\widehat {{D_5}}.\)
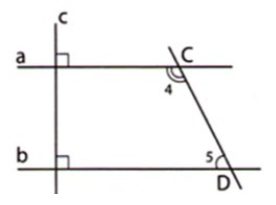
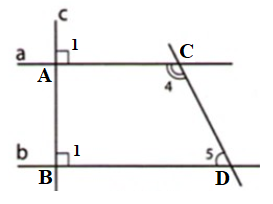
Theo đề bài: \(a \bot c\) và \(b \bot c\) nên \(\widehat {{A_1}} = \,\widehat {{B_1}} = {90^o}\), mà hai góc này ở vị trí đồng vị nên \(a//b.\)
Vì \(a//b\,\,(cmt)\) nên \(\widehat {{C_4}} + \widehat {{D_5}} = {180^o}\) (hai góc trong cùng phía bù nhau) (1)
Lại có: \(2\widehat {{C_4}} = 3\widehat {{D_5}}\) suy ra \(\widehat {{C_4}} = \dfrac{{3\widehat {{D_5}}}}{2}\) (2)
Thay (2) vào (1) ta được:
\(\begin{array}{l}\dfrac{{3\widehat {{D_5}}}}{2} + \widehat {{D_5}} = {180^o}\\ \Rightarrow \dfrac{5}{2}\widehat {{D_5}} = {180^o}\\ \Rightarrow \widehat {{D_5}} = {180^o}:\dfrac{5}{2} = {72^0}\end{array}\)
Vậy \(\widehat {{D_5}} = {72^o}\).

