Tia phân giác của một góc

Nếu  \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên C sai, D đúng.

Tia phân giác của một góc là tia nằm trong góc ấy và chia góc thành hai phần bằng nhau.

Vì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{80}^o}}}{2} = {40^o}\).

Ta có: \(\widehat {xOy}\) là góc bẹt nên \(\widehat {xOy} = {180^o}\).

Vì tia \(On\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOn} = \widehat {nOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{180}^o}}}{2} = {90^o}\).

Vì tia \(On\) là tia phân giác của \(\widehat {mOt}\) nên \(\widehat {mOn} = \widehat {nOt} = \dfrac{{\widehat {mOt}}}{2}\)

\( \Rightarrow \widehat {mOt} = 2.\widehat {mOn} = {2.55^o} = {110^o}\).

Vì tia \(OB\) là tia phân giác của góc \(AOC\) nên \(\widehat {AOB} = \widehat {BOC} = \dfrac{{\widehat {AOC}}}{2}\)

Do đó \(\widehat {AOC} = 2.\widehat {AOB} = {2.45^o} = {90^o}\)

Vậy góc \(AOC\) là góc vuông.

Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) nên ta có: \(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\)  

mà \(\widehat {AOC} = {75^0}\) nên \(\widehat {AOB} = {75^o}\); \(\,\widehat {BOC} = 2.\widehat {AOC} = {2.75^o} = {150^o}\)

Vậy \(\widehat {AOB} = {75^o};\,\widehat {BOC} = {150^o}\).

Theo câu trước ta có: tia \(OA\) là tia phân giác của \(\widehat {BOC}\) nên

\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) hay \(\widehat {BOC} = 2.\widehat {AOC} = {2.54^o} = {108^o}\).

Vì \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau và \(\widehat {AOB} + \widehat {AOC} = {54^o} + {54^o} = {108^0} < {180^o}\) nên tia \(OA\) nằm giữa hai tia \(OB;OC\).

Mặt khác: \(\widehat {AOB} = \widehat {AOC} = {54^0}\) (theo đề bài)

Do đó tia \(OA\) là tia phân giác của \(\widehat {BOC}\).

Vì \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau nên hai tia \(OC;OB\) thuộc cùng một nửa mặt phẳng có bờ chứa tia \(OA\). Lại có \(\widehat {AOB} < \widehat {AOC}\,\left( {\,do\,\,{{68}^o} < {{136}^o}} \right)\) nên tia \(OB\) nằm giữa hai tia \(OA\) và \(OC.\) (1)

Khi đó \(\widehat {AOB} + \widehat {BOC} = \widehat {AOC}\,\) hay \(\widehat {BOC} = \widehat {AOC} - \widehat {AOB} = {136^o} - {68^o} = {68^o}\)

Mà \(\widehat {AOB} = {68^0}\) suy ra \(\widehat {AOB} = \widehat {BOC} = {68^o}\) (2)

Từ (1) và (2) suy ra tia \(OB\) là tia phân giác của góc \(AOC.\)

Vậy A, B, D đúng và C sai. 

Vì tia \(Ot\)  là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{100^\circ }}{2} = 50^\circ \) 

Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \)

mà \(\widehat {xOy} = {112^o}\) suy ra \(\widehat {yOz} = {180^o} - \widehat {xOy} = {180^o} - {112^o} = {68^o}\).

Vì tia \(Ot\) là tia phân giác của \(\widehat {yOz}\) nên \(\widehat {zOt} = \dfrac{1}{2}\widehat {yOz} = \dfrac{1}{2}{.68^o} = {34^o}\)

Ta có: \(\widehat {zOt};\,\widehat {tOx}\) là hai góc kề bù nên \(\widehat {zOt} + \widehat {tOx} = 180^\circ  \Rightarrow \widehat {tOx} = 180^\circ  - \widehat {zOt}\)\( = 180^\circ  - 34^\circ  = 146^\circ .\)

Vậy \(\widehat {tOx} = 146^\circ .\)

Vì tia \(OM\) là tia phân của góc \(BOC\) nên \(\widehat {BOM} = \widehat {COM} = \dfrac{{\widehat {BOC}}}{2}\)

Mà \(\widehat {BOM} = {25^o}\) suy ra \(\widehat {COM} = {25^o}\); \(\widehat {BOC} = 2.\widehat {BOM} = 2.25^\circ  = 50^\circ \)

Vì tia \(OB\) là tia phân giác của \(\widehat {AOC}\) nên \(\widehat {BOC} = \dfrac{{\widehat {COA}}}{2}\) hay \(\widehat {COA} = 2.\widehat {BOC} = 2.50^\circ  = 100^\circ \).

Ta có: tia \(OM\) và tia \(OA\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(OC\) và \(\widehat {COM} < \widehat {COA}\,(do\,{25^o} < {100^o})\) nên tia \(OM\) nằm giữa hai tia \(OA\) và \(OC\).

Do đó \(\widehat {COM} + \widehat {MOA} = \widehat {COA} \Rightarrow \widehat {MOA} = \widehat {COA} - \widehat {COM} = {100^o} - {25^o} = {75^o}\).

+ Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 130^\circ \) nên \(\widehat {yOz} = 180^\circ  - \widehat {xOy} = 180^\circ  - 130^\circ  = 50^\circ \)

+ Vì tia \(Om\) nằm trong góc \(\widehat {yOz}\) nên tia \(Om\) nằm giữa hai tia \(Oy;Oz\) (1)

Khi đó \(\widehat {yOm} + \widehat {mOz} = \widehat {yOz}\) suy ra \(\widehat {mOz} = \widehat {yOz} - \widehat {yOm}\)

Theo câu trước ta có: \(\widehat {yOm} = 25^\circ \) nên \(\widehat {mOz} = 50^\circ  - 25^\circ  = 25^\circ \)

Do đó \(\widehat {mOz} = \widehat {yOm} = 25^\circ \) (2)

Từ (1) và (2) suy ra tia \(Om\) là tia phân giác của \(\widehat {yOz}\).

Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {tOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{130^\circ }}{2} = 65^\circ \).

Ta có: tia \(Oy\) và tia \(Om\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Ot\) và \(\widehat {tOy} < \widehat {tOm}\,(do\,{65^o} < {90^o})\) nên tia \(Oy\) nằm giữa hai tia \(Om;Ot\).

Do đó \(\widehat {tOy} + \widehat {yOm} = \widehat {tOm}\) hay \(\widehat {yOm} = \widehat {tOm} - \widehat {tOy} = 90^\circ  - 65^\circ  = 25^\circ \).

Vậy \(\widehat {yOm} = 25^\circ \).

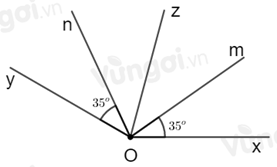
Theo câu trước ta có: \(\widehat {xOz} = 75^\circ \).

Vì tia \(Om\) và tia \(Oz\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\) và \(\widehat {xOm} < \widehat {xOz}\,\left( {35^\circ  < 75^\circ } \right)\)  nên

tia \(Om\) nằm giữa hai tia \(Oz\) và \(Ox\).

Do đó \(\widehat {xOm} + \widehat {mOz} = \widehat {xOz} \Rightarrow \widehat {mOz} = \widehat {xOz} - \widehat {xOm} = 75^\circ  - 35^\circ  = 40^\circ \)

Theo câu trước ta có: \(\widehat {nOz} = 40^\circ \) suy ra \(\widehat {mOz} = \widehat {nOz} = 40^\circ \) (1)

Vì \(On\) nằm giữa hai tia \(Oy;Oz\) (theo câu trước) và tia \(Om\) nằm giữa hai tia \(Ox;Oz\) (cmt) nên tia \(Oz\) nằm giữa hai tia \(Om;On\) (2)

Từ (1) và (2) suy ra tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).

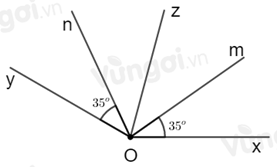
Vì tia \(Oz\) là tia phân giác của góc \(xOy\) nên \(\widehat {xOz} = \widehat {yOz} = \dfrac{1}{2}\widehat {xOy} = \dfrac{1}{2}.150^\circ  = 75^\circ \)

Ta có: tia \(On\) và tia \(Oz\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Oy\) và \(\widehat {yOn} < \widehat {yOz}\,\left( {35^\circ  < 75^\circ } \right)\) nên

tia \(On\) nằm giữa hai tia \(Oy;Oz\).

Do đó \(\widehat {yOn} + \widehat {nOz} = \widehat {yOz}\) \( \Rightarrow \widehat {nOz} = \widehat {yOz} - \widehat {yOn} = 75^\circ  - 35^\circ  = 40^\circ \).

Giả sử tia \(On\) là tia phân giác của góc \(yOm\). Khi đó ta có hình vẽ sau:

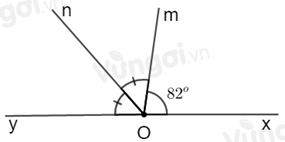
Vì \(\widehat {xOm};\widehat {yOm}\) là hai góc kề bù nên \(\widehat {xOm} + \widehat {yOm} = 180^\circ  \Rightarrow \widehat {yOm} = 180^\circ  - \widehat {xOm}\) \( = 180^\circ  - 82^\circ  = 98^\circ \).

Vì tia \(On\) là tia phân giác của góc \(yOm\) nên \(\widehat {yOn} = \dfrac{{\widehat {yOm}}}{2} = \dfrac{{{{98}^o}}}{2} = {49^o}\)

Vậy \(a = 49 \cdot \).

Vì \(\widehat {AOB};\,\widehat {BOC}\) là hai góc kề bù nên \(\widehat {AOC} = 180^\circ \) hay \(OA;OC\) là hai tia đối nhau.

Suy ra hai góc \(\widehat {MOC};\widehat {MOA}\) là hai góc kề bù nên \(\widehat {MOA} + \widehat {MOC} = 180^\circ   \,\,(1)\)

Theo đề bài ta có: \(5\widehat {COM} = 7\widehat {AOM} \Rightarrow \widehat {COM} = \dfrac{7}{5}\widehat {AOM}\) thay vào \((1)\) ta được:

\(\widehat {MOA} + \dfrac{7}{5}.\widehat {MOA} = 180^\circ  \Rightarrow \dfrac{{12}}{5}.\widehat {MOA} = 180^\circ \) suy ra \(\widehat {MOA} = {75^o}\)

Vì \(OM\) là tia phân giác của góc \(BOA\) nên \(\widehat {BOA} = 2.\widehat {MOA} = 2.75^\circ  = 150^\circ \)

Lại có: \(\widehat {AOB};\,\widehat {BOC}\) là hai góc kề bù nên \(\widehat {AOB} + \,\widehat {BOC} = 180^\circ \) suy ra \(\widehat {BOC} = 180^\circ  - \widehat {AOB} = 180^\circ  - 150^\circ  = 30^\circ \)

Vậy \(\widehat {BOC} = 30^\circ \).

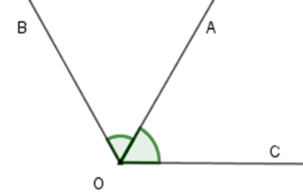
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) (theo câu trước) nên

\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) hay \(\widehat {BOC} = 2.\widehat {AOC} = 2.65^\circ  = 130^\circ \).