Cho góc bẹt \(xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) vẽ các tia \(Om;On\) sao cho \(\widehat {yOn} = a^\circ \,\left( {a < 180} \right)\) và \(\widehat {xOm} = 82^\circ .\) Với giá trị nào của \(a\) thì tia \(On\) là tia phân giác của \(\widehat {yOm}\).
Trả lời bởi giáo viên
Giả sử tia \(On\) là tia phân giác của góc \(yOm\). Khi đó ta có hình vẽ sau:
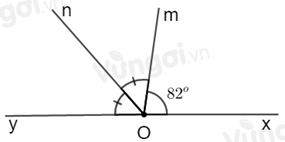
Vì \(\widehat {xOm};\widehat {yOm}\) là hai góc kề bù nên \(\widehat {xOm} + \widehat {yOm} = 180^\circ \Rightarrow \widehat {yOm} = 180^\circ - \widehat {xOm}\) \( = 180^\circ - 82^\circ = 98^\circ \).
Vì tia \(On\) là tia phân giác của góc \(yOm\) nên \(\widehat {yOn} = \dfrac{{\widehat {yOm}}}{2} = \dfrac{{{{98}^o}}}{2} = {49^o}\)
Vậy \(a = 49 \cdot \).
Hướng dẫn giải:
+ Tính \(\widehat {yOm}\)
+ Sử dụng điều kiện tia \(On\) là tia phân giác của \(\widehat {yOm}\) để tìm ra giá trị của a.

