Trả lời bởi giáo viên
Đáp án đúng: a
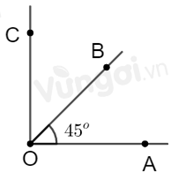
Vì tia OB là tia phân giác của góc AOC nên ^AOB=^BOC=^AOC2
Do đó ^AOC=2.^AOB=2.45o=90o
Vậy góc AOC là góc vuông.
Hướng dẫn giải:
Sử dụng:
+ Nếu tia Ot là tia phân giác của ^xOy thì ^xOt=^yOt=^xOy2
+ Kiến thức về các loại góc: Góc vuông là góc có số đo bằng 90o; Góc có số đo lớn hơn 0o và nhỏ hơn 90o là góc nhọn; Góc tù là góc có số đo lớn hơn 90o và nhỏ hơn 180o; Số đo của góc bẹt là 180o.

