Tia \(Om\) có phải là tia phân giác của \(\widehat {yOz}\) không? Vì sao?
+ Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \)
+ Vì tia \(Om\) nằm trong góc \(\widehat {yOz}\) nên tia \(Om\) nằm giữa hai tia \(Oy;Oz\) (1)
Do đó \(\widehat {yOm} + \widehat {mOz} = \widehat {yOz}\) suy ra \(\widehat {mOz} = \widehat {yOz} - \widehat {yOm} = 60^\circ - 30^\circ = 30^\circ \)
Hay \(\widehat {mOz} = \widehat {yOm} = 30^\circ \) (2)
Từ (1) và (2) suy ra tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Chọn câu đúng.
Trên nửa mặt phẳng bờ $Oy$, vì \(\widehat {xOz} = 55^\circ \) (theo câu trước) nên \(\widehat {xOm} < \widehat {xOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(Om\) nằm giữa hai tia \(Ox;Oz\)
Do đó \(\widehat {xOm} + \widehat {mOz} = \widehat {xOz} \Rightarrow \widehat {mOz} = 55^\circ - 30^\circ = 25^\circ \)
Suy ra \(\widehat {mOz} = \widehat {nOz} = 25^\circ \) (1)
Vì \(On\) nằm giữa hai tia \(Oy;Oz\) (theo câu trước) và tia \(Om\)nằm giữa hai tia \(Ox;Oz\) (cmt) nên tia \(Oz\)nằm giữa hai tia \(Om;On\) (2)
Từ (1) và (2) suy ra tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Chọn câu đúng.
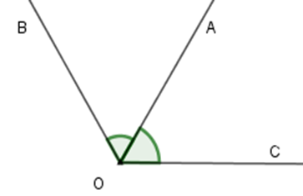
Vì \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau nên tia \(OA\) nằm giữa hai tia \(OB;OC\) mà \(\widehat {AOB} = \widehat {AOC} = {65^0}\) nên tia Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Tính \(\widehat {yOm}\).

Vì $Ot$ là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {tOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{120^\circ }}{2} = 60^\circ \).
Lại có tia \(Ot\) nằm trong góc \(xOy\) và tia \(Om\) nằm trong góc \(yOz\) mà hai góc \(\widehat {xOy};\,\widehat {yOz}\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Om;Ot\). Do đó \(\widehat {tOy} + \widehat {yOm} = \widehat {tOm}\) hay \(\widehat {yOm} = 90^\circ - \widehat {tOy} = 90^\circ - 60^\circ = 30^\circ \).
Vậy \(\widehat {yOm} = 30^\circ \).
Tính góc \(zOn\).
Vì tia \(Oz\) là tia phân giác của góc \(xOy\) nên \(\widehat {xOz} = \widehat {yOz} = \dfrac{1}{2}\widehat {yOx} = \dfrac{1}{2}.110^\circ = 55^\circ \)
Trên nửa mặt phẳng bờ $Oy$ có \(\widehat {yOn} < \widehat {yOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(On\) nằm giữa hai tia \(Oy;Oz\).
Do đó \(\widehat {yOn} + \widehat {nOz} = \widehat {zOy}\) \( \Rightarrow \widehat {zOn} = \widehat {zOy} - \widehat {yOn} = 55^\circ - 30^\circ = 25^\circ \).
Cho \(\widehat {xOy}\) là góc vuông có tia On là phân giác, số đo của \(\widehat {xOn}\) là:
Vì \(On\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOn} = \widehat {nOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Cho tia \(On\) là tia phân giác của \(\widehat {mOt}\). Biết \(\widehat {mOn} = {70^0}\), số đo của \(\widehat {mOt}\) là:
Vì tia \(On\) là tia phân giác của \(\widehat {mOt}\) nên \(\widehat {mOn} = \widehat {nOt} = \dfrac{{\widehat {mOt}}}{2}\)
\( \Rightarrow \widehat {mOt} = 2.\widehat {mOn} = 2.70^\circ = 140^\circ \).
Cho \(\widehat {AOB} = 90^\circ \) và tia \(OB\) là tia phân giác của góc \(AOC.\) Khi đó góc \(AOC\) là
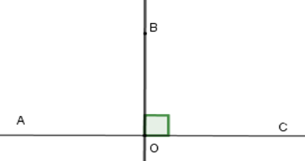
Vì tia \(OB\) là tia phân giác của góc \(AOC\) nên \(\widehat {AOB} = \widehat {BOC} = \dfrac{{\widehat {AOC}}}{2}\)
Do đó \(\widehat {AOC} = 2.\widehat {AOB} = 2.90^\circ = 180^\circ \)
Nên góc \(AOC\) là góc bẹt.
Cho \(\widehat {AOC} = {60^0}\). Vẽ tia \(OB\) sao cho \(OA\) là tia phân giác của \(\widehat {BOC}\). Tính số đo của \(\widehat {AOB}\) và \(\widehat {BOC}\).
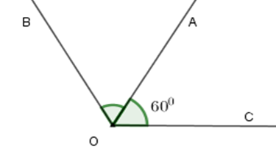
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) nên ta có
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) nên \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 2.\widehat {AOC} = 2.60^\circ = 120^\circ \)
Vậy \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \).
Cho \(\widehat {AOB} = {110^0}\) và \(\widehat {AOC} = {55^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau. Chọn câu sai.
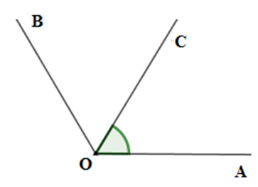
Vì \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau nên hai tia \(OC;OB\) thuộc cùng nửa mặt phẳng bờ là đường thẳng chứa tia \(OA\). Lại có \(\widehat {AOC} < \widehat {AOB}\,\left( {55^\circ < 110^\circ } \right)\) nên tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\) (1)
Từ đó \(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\,\) hay \(\widehat {COB} = \widehat {AOB} - \widehat {AOC} = 110^\circ - 55^\circ = 55^\circ \)
Suy ra \(\widehat {AOC} = \widehat {BOC} = 55^\circ \) (2)
Từ (1) và (2) suy ra tia \(OC\) là tia phân giác góc \(AOB.\)
Vậy A, B, D đúng và C sai.
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 120^\circ \) và tia \(Ot\) là tia phân giác của \(\widehat {yOz}.\) Tính số đo góc \(xOt.\)
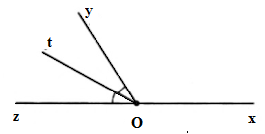
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \).
Lại có tia \(Ot\) là tia phân giác của \(\widehat {yOz}\) nên \(\widehat {zOt} = \dfrac{1}{2}\widehat {yOz} = \dfrac{1}{2}.60^\circ = 30^\circ \)
Lại có \(\widehat {zOt};\,\widehat {tOx}\) là hai góc kề bù nên \(\widehat {zOt} + \widehat {tOx} = 180^\circ \Rightarrow \widehat {tOx} = 180^\circ - \widehat {zOt}\)\( = 180^\circ - 30^\circ = 150^\circ .\)
Vậy \(\widehat {tOx} = 150^\circ .\)
Cho góc \(AOB\) và tia phân giác \(OC\) của góc đó. Vẽ tia phân giác \(OM\) của góc \(BOC.\) Biết \(\widehat {BOM} = 35^\circ .\) Tính số đo góc \(AOB.\)
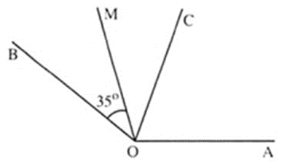
Vì tia \(OM\) là tia phân của góc \(BOC\)
nên \(\widehat {BOC} = 2.\widehat {BOM} = 2.35^\circ = 70^\circ \)
Lại có tia \(OC\) là tia phân giác của \(\widehat {AOB}\) nên \(\widehat {AOB} = 2.\widehat {BOC} = 2.70^\circ = 140^\circ \). Vậy \(\widehat {AOB} = 140^\circ \).
Cho góc bẹt \(xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) vẽ các tia \(Om;On\) sao cho \(\widehat {xOm} = a^\circ \,\left( {a < 180} \right)\) và \(\widehat {yOn} = 70^\circ .\) Với giá trị nào của \(a\) thì tia \(On\) là tia phân giác của \(\widehat {yOm}\).
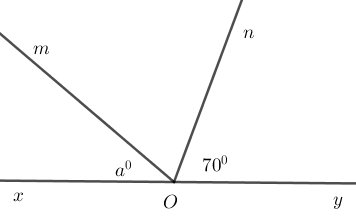
Giả sử tia \(On\) là tia phân giác của góc \(yOm\) thì \(\widehat {mOy} = 2.\widehat {yOn} = 2.70^\circ = 140^\circ \).
Mà hai góc \(\widehat {xOm};\widehat {yOm}\) là hai góc kề bù nên \(\widehat {xOm} + \widehat {yOm} = 180^\circ \)\( \Rightarrow \widehat {xOm} = 180^\circ - \widehat {yOm}\) \( = 180^\circ - 140^\circ = 40^\circ \).
Vậy \(a = 40 ^\circ\).
Cho \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau. Biết \(\widehat {AOB} = \widehat {AOC} = {65^0}\),
Chọn câu đúng.

Vì \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau nên tia \(OA\) nằm giữa hai tia \(OB;OC\) mà \(\widehat {AOB} = \widehat {AOC} = {65^0}\) nên tia Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Cho \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau. Biết \(\widehat {AOB} = \widehat {AOC} = {65^0}\),
Số đo góc \(BOC\) là
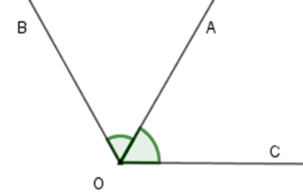
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) (theo câu trước) nên
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) hay \(\widehat {BOC} = 2.\widehat {AOC} = 2.65^\circ = 130^\circ \).
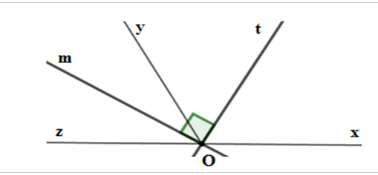
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\) sao cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\), vẽ tia Om trong góc \(\widehat {yOz}\) sao cho \(\widehat {tOm} = {90^0}\).
Tính \(\widehat {yOm}\).

Vì $Ot$ là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {tOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{120^\circ }}{2} = 60^\circ \).
Lại có tia \(Ot\) nằm trong góc \(xOy\) và tia \(Om\) nằm trong góc \(yOz\) mà hai góc \(\widehat {xOy};\,\widehat {yOz}\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Om;Ot\). Do đó \(\widehat {tOy} + \widehat {yOm} = \widehat {tOm}\) hay \(\widehat {yOm} = 90^\circ - \widehat {tOy} = 90^\circ - 60^\circ = 30^\circ \).
Vậy \(\widehat {yOm} = 30^\circ \).
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\) sao cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\), vẽ tia Om trong góc \(\widehat {yOz}\) sao cho \(\widehat {tOm} = {90^0}\).
Tia \(Om\) có phải là tia phân giác của \(\widehat {yOz}\) không? Vì sao?

+ Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \)
+ Vì tia \(Om\) nằm trong góc \(\widehat {yOz}\) nên tia \(Om\) nằm giữa hai tia \(Oy;Oz\) (1)
Do đó \(\widehat {yOm} + \widehat {mOz} = \widehat {yOz}\) suy ra \(\widehat {mOz} = \widehat {yOz} - \widehat {yOm} = 60^\circ - 30^\circ = 30^\circ \)
Hay \(\widehat {mOz} = \widehat {yOm} = 30^\circ \) (2)
Từ (1) và (2) suy ra tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
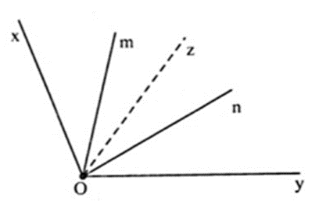
Cho góc \(xOy\) bằng \(110^\circ \) có tia \(Oz\) là tia phân giác. Vẽ các tia \(Om;On\) nằm trong góc \(xOy\) sao cho \(\widehat {xOm} = \widehat {yOn} = 30^\circ \).
Tính góc \(zOn\).

Vì tia \(Oz\) là tia phân giác của góc \(xOy\) nên \(\widehat {xOz} = \widehat {yOz} = \dfrac{1}{2}\widehat {yOx} = \dfrac{1}{2}.110^\circ = 55^\circ \)
Trên nửa mặt phẳng bờ $Oy$ có \(\widehat {yOn} < \widehat {yOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(On\) nằm giữa hai tia \(Oy;Oz\).
Do đó \(\widehat {yOn} + \widehat {nOz} = \widehat {zOy}\) \( \Rightarrow \widehat {zOn} = \widehat {zOy} - \widehat {yOn} = 55^\circ - 30^\circ = 25^\circ \).
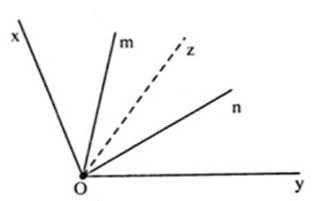
Cho góc \(xOy\) bằng \(110^\circ \) có tia \(Oz\) là tia phân giác. Vẽ các tia \(Om;On\) nằm trong góc \(xOy\) sao cho \(\widehat {xOm} = \widehat {yOn} = 30^\circ \).
Chọn câu đúng.

Trên nửa mặt phẳng bờ $Oy$, vì \(\widehat {xOz} = 55^\circ \) (theo câu trước) nên \(\widehat {xOm} < \widehat {xOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(Om\) nằm giữa hai tia \(Ox;Oz\)
Do đó \(\widehat {xOm} + \widehat {mOz} = \widehat {xOz} \Rightarrow \widehat {mOz} = 55^\circ - 30^\circ = 25^\circ \)
Suy ra \(\widehat {mOz} = \widehat {nOz} = 25^\circ \) (1)
Vì \(On\) nằm giữa hai tia \(Oy;Oz\) (theo câu trước) và tia \(Om\)nằm giữa hai tia \(Ox;Oz\) (cmt) nên tia \(Oz\)nằm giữa hai tia \(Om;On\) (2)
Từ (1) và (2) suy ra tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Cho hai góc kề bù \(\widehat {xOy};\,\widehat {xOz}\). Vẽ tia \(Ot\) là phân giác \(\widehat {xOy}\) và tia \(Ot'\) là phân giác \(\widehat {xOz}\). Tính \(\widehat {tOt'}\).
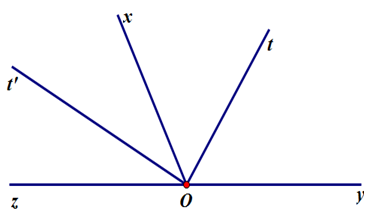
Vì tia \(Ot\) là phân giác \(\widehat {xOy}\) nên \(\widehat {yOt} = \widehat {xOt} = \dfrac{1}{2}\widehat {xOy}\) suy ra \(\widehat {xOy} = 2.\widehat {tOx}\) (1)
Và tia \(Ot'\) là phân giác \(\widehat {yOz}\) nên \(\widehat {zOt'} = \widehat {xOt'} = \dfrac{1}{2}\widehat {xOz}\) suy ra \(\widehat {xOz} = 2.\widehat {t'Ox}\) (2)
Mà \(\widehat {xOy};\,\widehat {xOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOz} = 180^\circ \) (3)
Từ (1) (2) (3) suy ra \(2.\widehat {tOx} + 2.\widehat {t'Ox} = 180^\circ \) suy ra \(2.\left( {\widehat {tOx} + \widehat {t'Ox}} \right) = 180^\circ \Rightarrow \widehat {tOx} + \widehat {t'Ox} = 90^\circ \) (4)
Lại có tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) và tia \(Ot'\) nằm giữa hai tia \(Ox;Oz\) nên tia \(Ox\) nằm giữa hai tia \(Ot;Ot'.\)
Do đó \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'}\) (5)
Từ (4) (5) suy ra \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'} = 90^\circ \).

