Cho hai tia \(Oy,Oz\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\), biết \(\widehat {xOy} = \alpha;\,\widehat {xOz} = \beta \,\left( {\alpha > \beta } \right).\) Tính \(\widehat {xOm}\) biết \(Om\) là phân giác góc \(yOz.\)
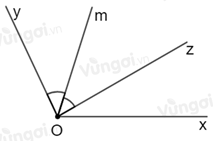
Ta có: hai tia \(Oy,Oz\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\) và \(\widehat {xOz} < \widehat {xOy}\,\left( {\beta < \alpha } \right)\) nên
tia \(Oz\) nằm giữa hai tia \(Oy,Ox\).
Do đó \(\widehat {xOz} + \widehat {zOy} = \widehat {xOy} \Rightarrow \widehat {zOy} = \widehat {xOy} - \widehat {xOz} = \alpha - \beta \)
Vì tia \(Om\) là tia phân giác của góc \(yOz\) nên \(\widehat {yOm} = \widehat {mOz} = \dfrac{{\widehat {yOz}}}{2} = \dfrac{{\alpha - \beta }}{2}\)
Ta có: hai tia \(Om,Ox\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Oy\) và \(\widehat {yOm} < \widehat {yOx}\,\,(do\,\dfrac{{\alpha - \beta }}{2} < \alpha )\) nên tia \(Om\) nằm giữa hai tia \(Oy,Ox\).
Do đó \(\widehat {xOm} + \widehat {mOy} = \widehat {xOy} \Rightarrow \widehat {xOm} = \widehat {xOy} - \widehat {mOy} = \alpha - \dfrac{{\alpha - \beta }}{2} = \dfrac{{\alpha + \beta }}{2}\).

