Câu hỏi:
2 năm trước
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $O$ và $O'$ lần lượt là tâm \(ABCD;\,A'B'C'D'\) . Hai mp $(ACC'A')$ và mp $\left( {BDD'B'} \right)$ cắt nhau theo đường nào?
Trả lời bởi giáo viên
Đáp án đúng: a
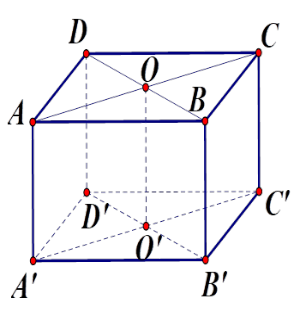
Gọi $O$ là giao điểm của $AC$ và $BD$ . Ta có \(O \in AC\) nên \(O \in {\rm{mp}}\left( {ACC'A'} \right)\), \(O \in BD\) nên \(O \in {\rm{mp}}\left( {BDD'B'} \right)\), do đó $O$ thuộc cả hai mặt phẳng trên. (1)
Gọi \(O'\) là giao điểm của \(A'C'\) và \(B'D'\) .
Chứng minh tương tự, \(O'\) thuộc cả hai mặt phẳng trên. (2)
Từ (1) và (2) suy ra hai mặt phẳng $(ACC'A')$ và mp $\left( {BDD'B'} \right)$ cắt nhau theo đường thẳng \(OO'\) .
Hướng dẫn giải:
Tìm đoạn thẳng thuộc cả hai mặt phẳng.