Phân số \(\dfrac{2}{-13}\) có số đối là:
Phân số đối của phân số \(\dfrac{2}{-13}\) là \(\dfrac{2}{13}\)
Số \(\dfrac{1}{-2}\) có số đối là:
Số đối của \(\dfrac{1}{-2}\) là \(\dfrac{1}{2}\)
Trong các phân số sau, phân số nào biểu diễn số hữu tỉ -0,35
Ta có:
\( - 0,35 = \frac{{ - 35}}{{100}} = \frac{{( - 35):5}}{{100:5}} = \frac{{ - 7}}{{20}}\)
Biểu diễn các số: \( - 0,4;\dfrac{8}{{20}};\dfrac{{12}}{{ - 20}};\dfrac{{ - 3}}{8}; - 0,375\) bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
Ta có:
\(\begin{array}{l} - 0,4 = \dfrac{{ - 4}}{{10}} = \dfrac{{ - 4:2}}{{10:2}} = \dfrac{{ - 2}}{5};\\\dfrac{8}{{20}} = \dfrac{{8:4}}{{20:4}} = \dfrac{2}{5};\\\dfrac{{12}}{{ - 20}} = \dfrac{{12:( - 4)}}{{( - 20):( - 4)}} = \dfrac{{ - 3}}{5};\\\dfrac{{ - 3}}{8};\\ - 0,375 = \dfrac{{ - 375}}{{1000}} = \dfrac{{( - 375):125}}{{1000:125}} = \dfrac{{ - 3}}{8}\end{array}\)
Vậy các số trên biểu diễn 4 số hữu tỉ khác nhau nên được biểu diễn bởi 3 điểm khác nhau trên trục số
Chọn câu đúng
Ta có \( - 6 \in \mathbb{Z};-6\notin\mathbb N \) nên D sai.
\(\dfrac{2}{3} \in \mathbb{Q};\,\dfrac{2}{3} \notin \mathbb{Z}\) nên B sai.
\( - \dfrac{9}{2} \in \mathbb{Q}\) nên C sai
\(\dfrac{3}{2} \in \mathbb{Q}\) nên A đúng.
Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\frac{5}{{ - 20}};\frac{{ - 5}}{{17}};\frac{1}{{ - 3}}\) theo thứ tự giảm dần:
Vì 20 > 17 nên \(\frac{5}{{20}} < \frac{5}{{17}}\), do đó \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}}\)
Vì \(\frac{5}{{17}} < \frac{5}{{15}} \Rightarrow \frac{{ - 5}}{{17}} > \frac{{ - 5}}{{15}} = \frac{1}{{ - 3}}\)
Vì \(\frac{7}{{20}} > \frac{7}{{21}} \Rightarrow \frac{{ - 7}}{{20}} < \frac{{ - 7}}{{21}} = \frac{1}{{ - 3}}\)
Do đó, \(\frac{5}{{ - 20}} > \frac{{ - 5}}{{17}} > \frac{1}{{ - 3}} > \frac{{ - 7}}{{20}}\)
Số nào dưới đây là số hữu tỉ dương?
\(\begin{array}{l}\dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3} > 0\,;\\\dfrac{{ - 2}}{5}\, < 0\,;\,\dfrac{{ - 5}}{{15}} < 0\,\,;\,\dfrac{2}{{ - 15}} < 0.\end{array}\)
Vậy số hữu tỉ dương là \(\dfrac{{ - 2}}{{ - 3}}.\)
Cho \(x = \frac{a}{{2{a^2} + 1}}\)
Với giá trị nào của a thì x là số hữu tỉ dương?
Ta có:
a2 \( \ge \)0, với mọi a nên 2a2 + 1 \( \ge \)1 > 0, với mọi a
Như vậy, để \(x = \frac{a}{{2{a^2} + 1}}\) > 0 thì a > 0
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) với:
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) trong đó \(a,b \in Z\,;b \ne 0.\)
Có mấy giá trị x nguyên thỏa mãn: \(\dfrac{{12}}{{ - 21}} > \dfrac{x}{7} > \dfrac{{ - 11}}{{14}}\)
Ta có: $\dfrac{{12}}{{ - 21}} > \dfrac{x}{7} > \dfrac{{ - 11}}{{14}}$
$\Leftrightarrow \dfrac{{ - 4}}{7} > \dfrac{x}{7} > \dfrac{{ - 11}}{{14}}$ (Rút gọn $\dfrac{{12}}{{ -21}}=\dfrac{{ - 4}}{7} $)
$ \Leftrightarrow \dfrac{{ - 8}}{{14}} > \dfrac{{2x}}{{14}} > \dfrac{{ - 11}}{{14}}$ (Quy đồng mẫu để được mẫu của 3 phân số đều là 14)
\(\begin{array}{l} \Rightarrow - 8 > 2x > - 11\\ \Leftrightarrow - 4 > x > - \dfrac{{11}}{2}\end{array}\)
\( \Leftrightarrow - 4 > x > - 5,5\)
Mà x nguyên nên \(x \in \{ - 5\} \)
Vậy có 1 giá trị x thỏa mãn
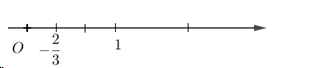
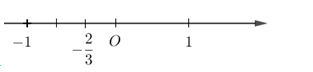
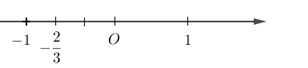
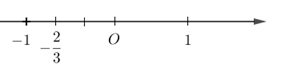
Số \( - \dfrac{2}{3}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
Biểu diễn số \( - \dfrac{2}{3}\) trên trục số ta được:
Thành tích chạy thi 100 m của 4 bạn An, Bình, Chi, Duy lần lượt là: 21,54 giây; \(\frac{1}{3}\)phút; \(\frac{{108}}{5}\) giây; \(20\frac{3}{8}\) giây.
Hỏi bạn nào chạy nhanh nhất?
Ta có: \(\frac{1}{3}\)phút = \(\frac{1}{3}\) . 60 = 20 giây
\(\frac{{108}}{5}\) giây = 21,6 giây
\(20\frac{3}{8}\) giây = 20,375 giây
Vì 20 < 20,375 < 21,54 < 21,6 nên Bình chạy nhanh nhất
Trong các phân số sau, phân số nào không bằng phân số $\dfrac{3}{4}$?
\(\dfrac{6}{9} = \dfrac{2}{3}\,;\,\dfrac{9}{{12}} = \dfrac{3}{4}\,;\,\dfrac{{ - 6}}{{ - 8}} = \dfrac{3}{4}\,;\,\dfrac{{ - 3}}{{ - 4}} = \dfrac{3}{4}.\)
Vậy phân số không bằng phân số $\dfrac{3}{4}$ là \(\dfrac{6}{9}.\)
Cho số hữu tỉ \(x = \frac{7}{{a + 2}}\)
Tìm tổng của các số nguyên a sao cho x là một số nguyên
Để x là số nguyên thì \(7 \vdots (n + 2) \Leftrightarrow n + 2 \in \) Ư (7) = {1; -1; 7; -7}
Ta có bảng sau:
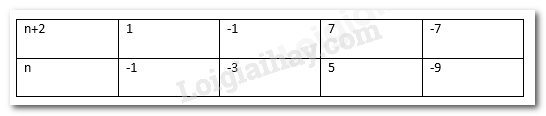
Tổng của các giá trị n đó là: (-1) + (-3) + 5 + (-9) = -8
Vậy có 4 giá trị n thỏa mãn điều kiện.
Cho các câu sau:
(I) Số hữu tỉ dương lớn hơn số hữu tỉ âm
(II) Số hữu tỉ dương lớn hơn số tự nhiên
(III) Số $0$ là số hữu tỉ âm
(IV) Số nguyên dương là số hữu tỉ.
Số các câu đúng trong các câu trên là
(I) đúng
(II) sai vì số hữu tỉ dương chưa chắc lớn hơn số tự nhiên. Ví dụ: \(\dfrac{5}{4} < 2\) .
(III) sai vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm
(IV) đúng vì mọi số nguyên dương đều là số hữu tỉ với mẫu số là \(1\).
Vậy có hai câu đúng.
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: \(\dfrac{{ - 12}}{{17}};\dfrac{{ - 3}}{{17}};\dfrac{{ - 16}}{{17}};\dfrac{{ - 1}}{{17}};\dfrac{{ - 11}}{{17}};\dfrac{{ - 14}}{{17}};\dfrac{{ - 9}}{{17}}.\)
Vì \( - 1 > - 3 > - 9 > - 11 > - 12 > - 14 > - 16\)
Nên ta có \(\dfrac{{ - 1}}{{17}} > \dfrac{{ - 3}}{{17}} > \dfrac{{ - 9}}{{17}} > \dfrac{{ - 11}}{{17}} > \dfrac{{ - 12}}{{17}} > \dfrac{{ - 14}}{{17}} > \dfrac{{ - 16}}{{17}}\)
Số hữu tỉ lớn nhất trong các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) là:
Phần bù với \(1\) của các số \(\dfrac{7}{8};\dfrac{2}{3};\dfrac{3}{4};\dfrac{{18}}{{19}};\dfrac{{27}}{{28}}\) lần lượt là \(\dfrac{1}{8};\,\dfrac{1}{3};\dfrac{1}{4};\dfrac{1}{{19}};\dfrac{1}{{28}}\)
Mà \(28 > 19 > 8 > 4 > 3\) nên \(\dfrac{1}{{28}} < \dfrac{1}{{19}} < \dfrac{1}{8} < \dfrac{1}{4} < \dfrac{1}{3}\)
Suy ra \(\dfrac{{27}}{{28}} > \dfrac{{18}}{{19}} > \dfrac{7}{8} > \dfrac{3}{4} > \dfrac{2}{3}\)
Số hữu tỉ lớn nhất là: \(\dfrac{{27}}{{28}}\)
So sánh hai số \(x = \dfrac{2}{{ - 5}}\) và \(y = \dfrac{{ - 3}}{{13}}\)
Ta có \(x = \dfrac{2}{{ - 5}} = \dfrac{{2.\left( { - 13} \right)}}{{\left( { - 5} \right).\left( { - 13} \right)}} = \dfrac{{ - 26}}{{65}}\) và $y = \dfrac{{ - 3}}{{13}} = \dfrac{{ - 3.5}}{{13.5}} = \dfrac{{ - 15}}{{65}}$
Mà \( - 26 < - 15 \Rightarrow \dfrac{{ - 26}}{{65}} < \dfrac{{ - 15}}{{65}}\) hay \(x < y\) .
So sánh \(x = \dfrac{{2002}}{{2003}}\) và \(y = \dfrac{{14}}{{13}}\)
Ta có \(x = \dfrac{{2002}}{{2003}} < \dfrac{{2003}}{{2003}} = 1\) hay \(x < 1\)
Và \(y = \dfrac{{14}}{{13}} > \dfrac{{13}}{{13}} = 1\) hay \(y > 1\)
Từ đó suy ra \(y > 1 > x\) hay \(y > x\) .
Biểu diễn các số: $\dfrac{1}{4}$; $0,25$; $\dfrac{{ - \,25}}{{ - 100}}$; $\dfrac{5}{{20}}$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
$0,25 = \dfrac{{25}}{{100}} = \dfrac{1}{4};\dfrac{{ - 25}}{{ - 100}} = \dfrac{1}{4};\dfrac{5}{{20}} = \dfrac{1}{4}.$
Nên \(\dfrac{1}{4} = 0,25 = \dfrac{{ - 25}}{{ - 100}} = \dfrac{5}{{20}}\)
Do đó các số \(\dfrac{1}{4};0,25\,;\,\dfrac{{ - 25}}{{ - 100}}\,;\,\dfrac{5}{{20}}\) được biểu diễn cùng một điểm trên trục số.