Cho tam giác ABC bất kì và điểm D nằm trên cạnh BC.
Khẳng định sai là:
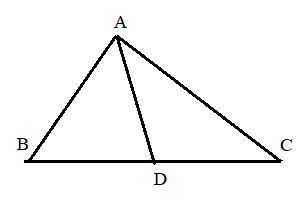
Áp dụng định lí tổng số đo 3 góc trong 3 tam giác ABD, ACD và ABC, ta được:
^BAD+^ABD+^ADB=180∘
^CAD+^ADC+^ACB=180∘
^BAC+^ACD+^ABD=180∘
Vậy A,C,D đúng
Cho tam giác ABC có ˆA=86∘;ˆB=62∘. Số đo góc C là:
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
ˆA+ˆB+ˆC=180∘⇒86∘+62∘+ˆC=180∘⇒ˆC=180∘−86∘−62∘=32∘
Cho tam giác ABC vuông tại A. Khi đó
Vì tam giác ABC vuông tại A nên ˆB+ˆC=90∘.
Cho hình sau. Tính số đo x:
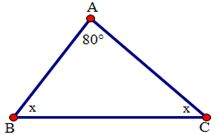
Áp dụng tính chất tổng ba góc trong tam giác ABC, ta có:
ˆA+ˆB+ˆC=1800⇒ˆB+ˆC=1800−ˆA=1800−800=1000.
Hay x+x=1000⇒2x=1000⇒x=500
Cho tam giác ABC có ˆA=960,ˆC=500. Số đo góc B là:
Xét tam giác ABC có :ˆA+ˆB+ˆC=1800⇒ˆB=1800−(ˆA+ˆC)=1800−(960+500)=340.
Cho tam giác ABC có ˆA=500,ˆB=700. Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
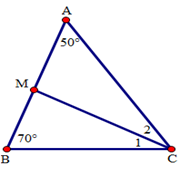
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
ˆA+ˆB+ˆC=1800⇒ˆC=1800−(ˆA+ˆB)=1800−(500+700)=600.
Do CM là tia phân giác của góc ACB nên ^C1=^C2=ˆC2=6002=300.
Áp dụng định lí tổng ba góc trong tam giác BMC có:
ˆB+^BMC+ˆC1=1800⇒^BMC=1800−(ˆB+^C1)=1800−(700+300)=800
Cho hình vẽ sau. Tính số đo x.
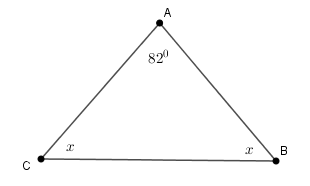
Xét tam giác ABC có :ˆA+ˆB+ˆC=1800⇒ˆB+ˆC=1800−ˆA=1800−820=980.
Hay x+x=980⇒2x=980⇒x=490
Tam giác ABC có ˆA=800,ˆB−ˆC=500. Số đo góc B và góc C lần lượt là:
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
ˆA+ˆB+ˆC=180∘⇒ˆB+ˆC=180∘−80∘=100∘
Ta có:
ˆC=(100∘−50∘):2=25∘;ˆB=ˆC+50∘=25∘+50∘=75∘
Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc .
Giả sử tam giác ABC có ba góc bằng nhau ˆA=ˆB=ˆC
Lại có ˆA+ˆB+ˆC=1800⇒ˆA+ˆA+ˆA=180∘⇒3ˆA=180∘⇒ˆA=180∘:3⇒ˆA=60∘.
Vậy ˆA=ˆB=ˆC=60∘.
Cho hình vẽ sau. Tính số đo góc x:
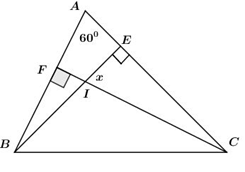
Áp dụng tính chất tổng ba góc trong tam giác ACF có :ˆA+^ACF+^AFC=1800⇔600+^ACF+900=1800
⇒^ACF=1800−600−900=300.
Áp dụng tính chất tổng ba góc trong ΔIEC ta có: ^IEC+^ECI+^EIC=1800⇔300+x+900=1800
⇒x=1800−300−900=600.
Cho hình sau. Tính số đo x.
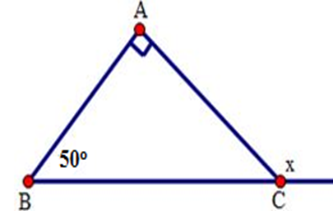
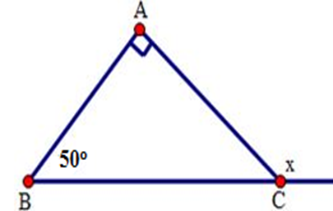
Ta có x là số đo góc ngoài tại đỉnh C của tam giác ABC nên
x=ˆA+ˆB=500+900=1400.
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
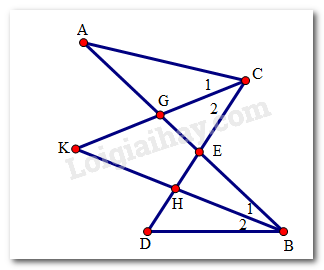
Gọi G là giao điểm của CK và AE, H là giao điểm của BK và DE.
Xét tam giác KGB và tam giác AGC và theo tính chất góc ngoài của tam giác ta có:{ˆK+^B1=^AGKˆA+^C1=^AGK⇒ˆK+^B1=ˆA+^C1 (1)
Xét tam giác KHC và tam giác DHB và theo tính chất góc ngoài của tam giác ta có:{ˆK+^C2=^EHBˆD+^B2=^EHB⇒ˆK+^C2=ˆD+^B2 (2)
Do ^B1=^B2 (BK là tia phân giác của góc DBA);
^C1=^C2 ( CK là tia phân giác của góc ACD).
Nên cộng (1) với (2) ta được 2ˆK=ˆA+ˆD, do đó ˆK=ˆA+ˆD2 hay ^BKC=^BAC+^BDC2
Cho tam giác ABC biết rằng số đo các góc ˆA;ˆB;ˆC tỉ lệ với 2;3;4. Tính ˆB.
Theo tính chất tổng 3 góc của tam giác ta có: ˆA+ˆB+ˆC=1800.
Theo đề bài ta có: ˆA:ˆB:ˆC=2:3:4⇒ˆA2=ˆB3=ˆC4.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
ˆA2=ˆB3=ˆC4=ˆA+ˆB+ˆC2+3+4=18009=200.⇒{ˆA=200.2=400ˆB=200.3=600ˆC=200.4=800.
Vậy các góc của tam giác ABC là: ˆA=400;ˆB=600;ˆC=800.
Tam giác ABC có ˆB+ˆC=ˆA và ˆC=2ˆB. Tia phân giác của góc C cắt AB ở D. Tính ^ADC
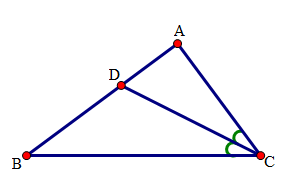
Xét tam giác ABC có ˆA+ˆB+ˆC=1800 mà ˆB+ˆC=ˆA, do đó 2ˆA=1800⇒ˆA=900.
Trong tam giác ABC do ˆA=900 nên ˆB+ˆC=90∘. Mà ˆC=2ˆB do đó 3ˆB=900⇒ˆB=300nên ˆC=600
Do CD là tia phân giác của góc ACD nên ^ACD=^DCB=ˆC:2=60∘:2=30∘
Xét tam giác ADC có: ˆA+^ADC+^ACD=1800⇒^ADC=1800−(ˆA+^ACD)=1800−(300+90∘)=60∘
Tam giác ABC có ˆA=1000,ˆB−ˆC=400. Số đo góc B và góc C lần lượt là:
Xét tam giác ABC có :ˆA+ˆB+ˆC=1800⇒ˆB+ˆC=1800−1000=800(1)
Theo đề bài ta có:ˆB−ˆC=400 (2)
Từ (1) ta có: ˆC=800−ˆB.
Thế vào (2) ta được: ˆB−(800−ˆB)=400⇔2.ˆB=400+800⇔ˆB=12002=600.
⇒ˆC=800−600=200.
Khẳng định nào sau đây là sai?
Các khẳng định A,B,D đúng.
Khẳng định C sai vì: Góc lớn nhất trong tam giác nhọn là một góc nhọn, góc lớn nhất trong tam giác vuông là góc vuông.
Cho tam giác ABC có ˆA=500,ˆB=700. Tia phân giác của góc C cắt cạnh AB tại M. Tính ^AMC và ^BMC.
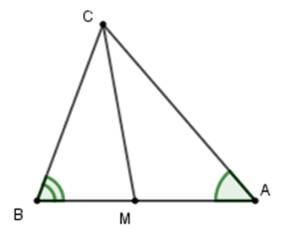
Xét tam giác ABC có ˆA+ˆB+^BCA=180∘(định lý tổng ba góc trong tam giác) mà ˆA=500,ˆB=700. Suy ra ^BCA=180∘−50∘−70∘=60∘.
Vì CM là tia phân giác của góc BCA nên ^BCM=^ACM=^BCA2=60∘2=30∘
Ta có ^AMC là góc ngoài tại đỉnh M của tam giác BCM nên ta có
^AMC=ˆB+^BCM=70∘+30∘=100∘
Lại có ^AMC+^BMC=180∘ (hai góc kề bù) suy ra ^BMC=180∘−^AMC=80∘.
Vậy ^AMC=100∘;^BMC=80∘.
Cho hình sau. Tính số đo x:
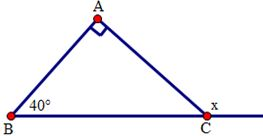
Ta có góc cần tính là góc ngoài tại đỉnh C của tam giác ABC nên:
x=ˆA+ˆB=90∘+40∘=130∘
Cho tam giác ABC có ˆB=800,3ˆA=2ˆC.Tính ˆA và ˆC?
Xét tam giác ABC có ˆB=800. Theo định lý về tổng ba góc trong tam giác ta có
ˆA+ˆB+ˆC=180∘⇒ˆA+ˆC=180∘−ˆB⇒ˆA+ˆC=100∘.
Lại có 3ˆA=2ˆC⇒ˆA2=ˆC3
Áp dụng tính chất dãy tỉ số bằng nhau ta được
ˆA2=ˆC3=ˆA+ˆC2+3=100∘5=20∘
Suy ra ˆA=40∘;ˆC=60∘.
Cho hình vẽ sau. Tính số đo góc x?
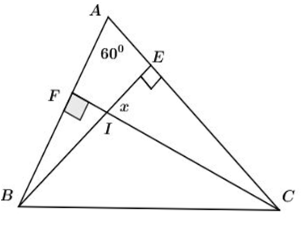
Xét tam giác ACF có :ˆA+^ACF+^AFC=1800⇔600+^ACF+900=1800
⇒^ACF=1800−600−900=300.
Xét ΔIEC ta có: ^IEC+^ECI+^EIC=1800⇔300+x+900=1800
⇒x=1800−300−900=600.

