Tổng các góc trong một tam giác

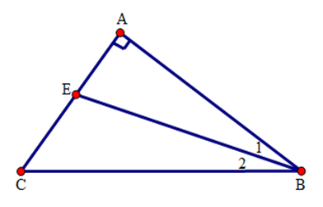
Góc $BEC$  là góc ngoài ở đỉnh $E$  của tam giác $AEC$ nên \(\widehat {BEC} = \widehat A + \widehat {ABE} = {90^ \circ } + \widehat {ABE} > {90^ \circ }\)

Vậy góc $BEC$ là góc tù nên \(\widehat {BEC} > \widehat {EBA}\) và \(\widehat {BEC} > \widehat {ECB}.\)

Vậy A, C, D đúng, B sai.

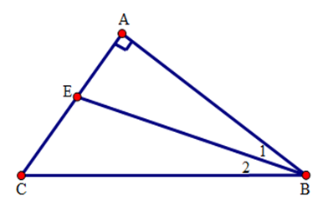
Theo giả thiết \(\widehat C - \widehat B = {26^0}\).

Mặt khác do tam giác $ABC$  vuông tại $A$  nên \(\widehat B + \widehat C = {90^ \circ }\)

Từ đó ta có \(\widehat C = \dfrac{{90^\circ  + 26^\circ }}{2} = {58^0} \Rightarrow \widehat B = {32^0}\).

Do $BE$  là tia phân giác của góc $ABC$  nên \(\widehat {{B_1}} = \widehat {{B_2}} = {16^0}\)

Sử dụng tinh chất góc ngoài của tam giác ta tìm được \(\widehat {AEB} = \widehat C + \widehat {{B_2}} = {58^0} + 16^\circ  = 74^\circ .\)

Và \(\widehat {BEC} = \widehat A + \widehat {{B_1}} = 106^\circ .\)

Vậy \(\widehat {AEB} = 74^\circ ;\,\widehat {BEC} = 106^\circ .\)

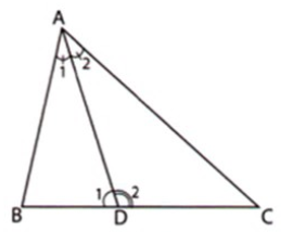
Ta có: \(\widehat {{D_2}}\) là góc ngoài tại đỉnh \(D\) của tam giác \(ABD\) nên \(\widehat {{D_2}} = \widehat {{A_1}} + \widehat B\,\,\,\,\,(1)\)

Ta có: \(\widehat {{D_1}}\) là góc ngoài tại đỉnh \(D\) của tam giác \(ADC\) nên \(\widehat {{D_1}} = \widehat {{A_2}} + \widehat C\,\,\,\,\,\,(2)\)

Từ (1) và (2) ta có:

\(\widehat {{D_2}} - \widehat {{D_1}} = \widehat {{A_1}} - \widehat {{A_2}} + \widehat B - \widehat C = \left( {\widehat {{A_1}} - \widehat {{A_2}}} \right) + \left( {\widehat B - \widehat C} \right)\)

Vì \(AD\) là tia phân giác \(\widehat A\) nên \(\widehat {{A_1}} = \widehat {{A_2}}\) và \(\widehat B - \widehat C = {20^0}\,\,(gt)\) suy ra \(\widehat {{D_2}} - \widehat {{D_1}} = {20^o}\,\,\,\,\,\,(3)\)

Mặt khác \(\widehat {{D_1}}\) và \(\widehat {{D_2}}\) là hai góc kề bù nên \(\widehat {{D_1}} + \widehat {{D_2}} = {180^o}\,\,\,\,\,(4)\)

Từ (3) và (4) suy ra \(\widehat {{D_2}} = \left( {{{20}^o} + {{180}^o}} \right):2 = {100^o};\,\,\widehat {{D_1}} = {180^o} - {100^o} = {80^o}.\)

Vậy \(\widehat {{D_1}} = {80^o};\,\widehat {{D_2}} = {100^o}.\)