Góc ở vị trí đặc biệt. Tia phân giác của một góc
Sách kết nối tri thức với cuộc sống
Cho Ot là tia phân giác của ^xOy. Biết ^xOy=1000, số đo của ^xOt là:
Vì tia Ot là tia phân giác của ^xOy thì ^xOt=^yOt=^xOy2=100∘2=50∘
Hai đường thẳng zz’ và tt’ cắt nhau tại A. Góc đối đỉnh với ^zAt′ là:
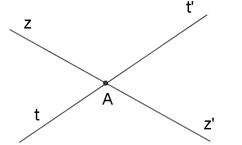
Vì hai đường thẳng zz′ và tt′ cắt nhau tại A nên Az′ là tia đối của tia Az,At′ là tia đối của tia At. Vậy góc đối đỉnh với ^zAt′ là ^z′At.
Cho ^xOy là góc vuông có tia On là phân giác, số đo của ^xOn là:
Vì On là tia phân giác của ^xOy nên ^xOn=^nOy=^xOy2=90∘2=45∘
Cho hai đường thẳng xx′ và yy′ cắt nhau tại O sao cho ^xOy=135∘ . Chọn câu đúng:
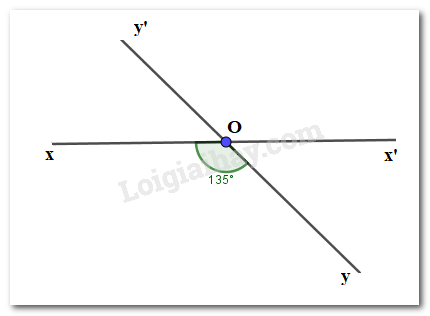
Vì hai đường thẳng xx′ và yy′ cắt nhau tại O nên Ox′ là tia đối của tia Ox;Oy′ là tia đối của tia Oy.
Suy ra ^xOy và ^x′Oy′ ; ^x′Oy và ^xOy′ là hai cặp góc đối đỉnh.
Do đó ^x′Oy′=^xOy=135∘ và ^x′Oy=^xOy′
Lại có ^xOy và ^x′Oy là hai góc kề bù nên
^xOy+^x′Oy=180∘
⇒45∘+^x′Oy=180∘⇒^x′Oy=180∘−135∘=45∘⇒45∘+^x′Oy=180∘⇒^x′Oy=180∘−135∘=45∘
Vậy ^x′Oy′=^xOy=135∘ và ^x′Oy=^xOy′=45∘.
Cho tia On là tia phân giác của ^mOt. Biết ^mOn=700, số đo của ^mOt là:
Vì tia On là tia phân giác của ^mOt nên ^mOn=^nOt=^mOt2
⇒^mOt=2.^mOn=2.70∘=140∘.
Cho góc xBy đối đỉnh với góc x′By′ và ^xBy=60∘ . Tính số đo góc x′By′.
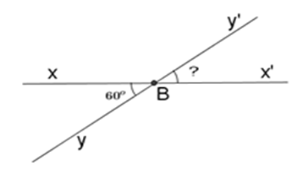
Vẽ ^x′By′ là góc đối đỉnh với ^xBy. Khi đó:
^x′By′=^xBy=60o (tính chất hai góc đối đỉnh)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mc). Biết ^aMc=5.^bMc. Tính số đo ^aMc ?
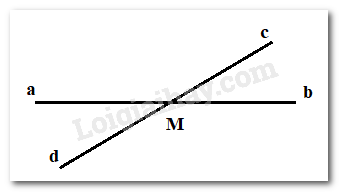
Ta có : ^aMc+^bMc=180∘ ( 2 góc kề bù)
Mà ^aMc=5.^bMc
⇒5.^bMc+^bMc=180∘⇒6.^bMc=180∘⇒^bMc=180∘:6=30∘⇒^aMc=5.30∘=150∘
⇒5.^bMc+^bMc=180∘⇒6.^bMc=180∘⇒^bMc=180∘:6=30∘⇒^aMc=5.30∘=150∘
Cho ^AOB=90∘ và tia OB là tia phân giác của góc AOC. Khi đó góc AOC là
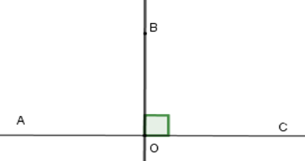
Vì tia OB là tia phân giác của góc AOC nên ^AOB=^BOC=^AOC2
Do đó ^AOC=2.^AOB=2.90∘=180∘
Nên góc AOC là góc bẹt.
Cho ^ABC=56o. Vẽ ^ABC′ kề bù với ^ABC; ^C′BA′ kề bù với ^ABC′. Tính số đo ^C′BA′.
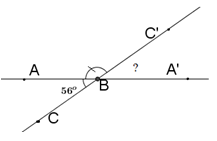
Vì góc ABC′ kề bù với góc ABC nên BC′ là tia đối của tia BC.
Vì góc C′BA′ kề bù với góc ABC′ nên BA′ là tia đối của tia BA.
Do đó, góc C′BA′ và góc ABC đối đỉnh.
⇒^C′BA′=^ABC=56o
Cho ^AOC=600. Vẽ tia OB sao cho OA là tia phân giác của ^BOC. Tính số đo của ^AOB và ^BOC.
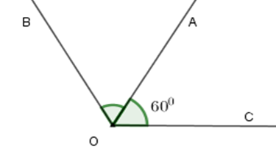
Vì tia OA là tia phân giác của ^BOC nên ta có
^AOB=^AOC=^BOC2 nên ^AOB=60∘;^BOC=2.^AOC=2.60∘=120∘
Vậy ^AOB=60∘;^BOC=120∘.
Cho cặp góc đối đỉnh ^tOz và ^t′Oz′ (Oz và Oz′ là hai tia đối nhau). Biết ^tOz′=4.^tOz. Tính các góc ^tOz và ^t′Oz′.
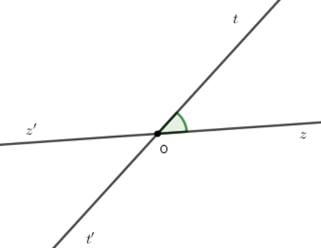
Ta có ^zOt+^tOz′=180∘ (hai góc kề bù) mà ^tOz′=4.^tOz ⇒^zOt+4.^zOt=180∘ ⇒5.^zOt=180∘⇒^zOt=36∘
Vì ^tOz và ^t′Oz′ là hai góc đối đỉnh nên ^zOt=^z′Ot′=36∘.
Vẽ góc xOy có số đo bằng 125o. Vẽ góc x′Oy′ đối đỉnh với góc xOy. Viết tên các góc có số đo bằng 55o.
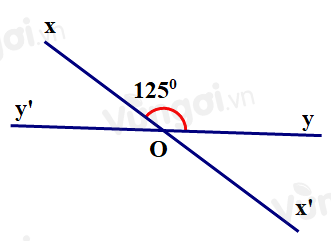
Vì hai đường thẳng xx′ và yy′ cắt nhau tại O nên Ox′ là tia đối của tia Ox;Oy′ là tia đối của tia Oy.
Suy ra ^xOy và ^x′Oy′ ; ^x′Oy và ^xOy′ là hai cặp góc đối đỉnh.
Do đó ^x′Oy′=^xOy=125∘ và ^x′Oy=^xOy′
Lại có ^xOy và ^x′Oy là hai góc ở vị trí kề bù nên
^xOy+^x′Oy=180∘
⇒125∘+^x′Oy=180∘⇒^x′Oy=180∘−125∘=55∘
Hai góc có số đo bằng 55o là : ^xOy′;^x′Oy
Cho ^AOB=1100 và ^AOC=550 sao cho ^AOB và ^AOC không kề nhau. Chọn câu sai.
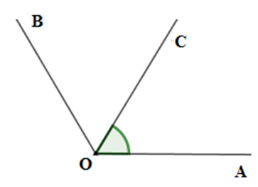
Vì ^AOB và ^AOC không kề nhau nên hai tia OC;OB thuộc cùng nửa mặt phẳng bờ là đường thẳng chứa tia OA. Lại có ^AOC<^AOB(55∘<110∘) nên tia OC nằm giữa hai tia OA và OB. (1)
Từ đó ^AOC+^COB=^AOB hay ^COB=^AOB−^AOC=110∘−55∘=55∘
Suy ra ^AOC=^BOC=55∘ (2)
Từ (1) và (2) suy ra tia OC là tia phân giác góc AOB.
Vậy A, B, D đúng và C sai.
Cho tia Ok là tia phân giác của ^mOn= 70o . Tính ^nOk
Vì Ok là tia phân giác của ^mOn nên ^mOk=^nOk=12.^mOn=12.70∘=35∘
Cho ^xOy và ^yOz là hai góc kề bù. Biết ^xOy=120∘ và tia Ot là tia phân giác của ^yOz. Tính số đo góc xOt.
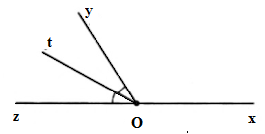
Vì ^xOy và ^yOz là hai góc kề bù nên ^xOy+^yOz=180∘ mà ^xOy=120∘ nên ^yOz=180∘−120∘=60∘.
Lại có tia Ot là tia phân giác của ^yOz nên ^zOt=12^yOz=12.60∘=30∘
Lại có ^zOt;^tOx là hai góc kề bù nên ^zOt+^tOx=180∘⇒^tOx=180∘−^zOt=180∘−30∘=150∘.
Vậy ^tOx=150∘.
Hai đường thẳng MN và PQ cắt nhau tại O, tạo thành ^MOP=50∘ . Cho tia OK là tia phân giác của ^PON. Chọn khẳng định sai.
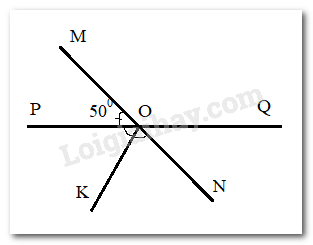
Ta có : ^QON=^MOP=50∘ ( 2 góc đối đỉnh)
^MOQ+^QON=180o ( 2 góc kề bù)
^MOP+^PON=180∘ ( 2 góc kề bù)
⇒50∘+^PON=180∘⇒^PON=180∘−50∘=130∘
Vì OK là tia phân giác của ^PON
⇒^POK=^NOK=12.^PON=12.130∘=65∘
Vậy khẳng định A, C, D đúng, B sai
Cho góc AOB và tia phân giác OC của góc đó. Vẽ tia phân giác OM của góc BOC. Biết ^BOM=35∘. Tính số đo góc AOB.
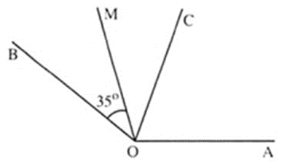
Vì tia OM là tia phân của góc BOC
nên ^BOC=2.^BOM=2.35∘=70∘
Lại có tia OC là tia phân giác của ^AOB nên ^AOB=2.^BOC=2.70∘=140∘. Vậy ^AOB=140∘.
Hai đường thẳng xy và x'y' cắt nhau tại O. Biết \widehat {xOx'} = {70^o}. Ot là tia phân giác của góc xOx’. Ot' là tia đối của tia Ot. Tính số đo góc yOt'.
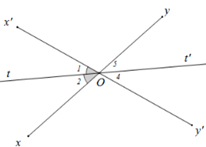
Vì Ot là tia phân giác của góc xOx' nên \widehat {xOt} = \widehat {tOx'} = \frac{1}{2}\widehat {xOx'} = \frac{1}{2}{.70^o} = {35^o}
Vì Oy là tia đối của Ox,Ot' là tia đối của Ot
\Rightarrow \widehat {yOt'} = \widehat {xOt} = {35^o} (tính chất hai góc đối đỉnh).
Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om;On sao cho \widehat {xOm} = a^\circ \,\left( {a < 180} \right) và \widehat {yOn} = 70^\circ . Với giá trị nào của a thì tia On là tia phân giác của \widehat {yOm}.
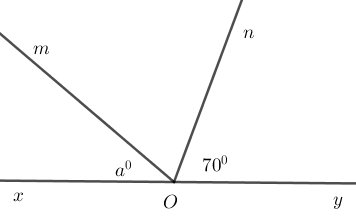
Giả sử tia On là tia phân giác của góc yOm thì \widehat {mOy} = 2.\widehat {yOn} = 2.70^\circ = 140^\circ .
Mà hai góc \widehat {xOm};\widehat {yOm} là hai góc kề bù nên \widehat {xOm} + \widehat {yOm} = 180^\circ \Rightarrow \widehat {xOm} = 180^\circ - \widehat {yOm} = 180^\circ - 140^\circ = 40^\circ .
Vậy a = 40 ^\circ.
Cho \widehat {xOy},\widehat {yOz} là 2 góc kề bù. Góc xOy có số đo là 60o . Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn
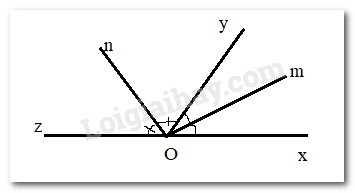
Ta có: \widehat {xOy} + \widehat {yOz} = 180^\circ ( 2 góc kề bù)
\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ
Vì Om là tia phân giác của góc xOy nên \widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ
Vì On là tia phân giác của góc yOz nên \widehat {yOn} = \widehat {nOz} = \frac{1}{2}.\widehat {yOz} = \frac{1}{2}.120^\circ = 60^\circ
Vì Oy nằm giữa 2 tia Om và On nên \widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ

