Câu hỏi:
2 năm trước
Cho \(\widehat {AOB} = {110^0}\) và \(\widehat {AOC} = {55^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau. Chọn câu sai.
Trả lời bởi giáo viên
Đáp án đúng: c
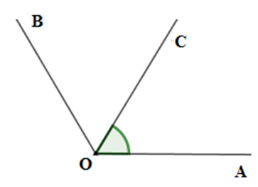
Vì \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau nên hai tia \(OC;OB\) thuộc cùng nửa mặt phẳng bờ là đường thẳng chứa tia \(OA\). Lại có \(\widehat {AOC} < \widehat {AOB}\,\left( {55^\circ < 110^\circ } \right)\) nên tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\) (1)
Từ đó \(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\,\) hay \(\widehat {COB} = \widehat {AOB} - \widehat {AOC} = 110^\circ - 55^\circ = 55^\circ \)
Suy ra \(\widehat {AOC} = \widehat {BOC} = 55^\circ \) (2)
Từ (1) và (2) suy ra tia \(OC\) là tia phân giác góc \(AOB.\)
Vậy A, B, D đúng và C sai.
Hướng dẫn giải:
+ Sử dụng dấu hiệu nhận biết tia nằm giữa hai tia
+ Tính góc \(BOC\)
+ Sử dụng định nghĩa tia phân giác
Câu hỏi khác
- Bài tập trắc nghiệm Góc ở vị trí đặc biệt. Tia phân giác của một góc môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Hai đường thẳng song song và dấu hiệu nhận biết môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Tiên đề Euclid. Tính chất của hai đường thẳng song song môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Định lí và chứng minh định lí môn Toán lớp 7 sách KNTTVCS có lời giải
