Câu hỏi:
2 năm trước
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
Trả lời bởi giáo viên
Đáp án đúng: d
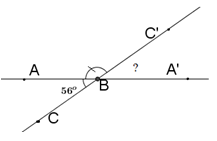
Vì góc \(ABC'\) kề bù với góc \(ABC\) nên \(BC'\) là tia đối của tia \(BC.\)
Vì góc \(C'BA'\) kề bù với góc \(ABC'\) nên \(BA'\) là tia đối của tia \(BA.\)
Do đó, góc \(C'BA'\) và góc \(ABC\) đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Hướng dẫn giải:
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)

