Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(O\), tạo thành \(\widehat {MOP} = 50^\circ \) . Cho tia OK là tia phân giác của \(\widehat {PON}\). Chọn khẳng định sai.
Trả lời bởi giáo viên
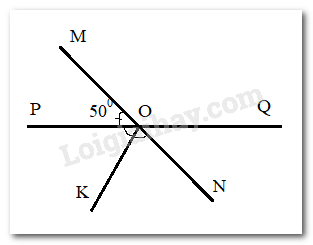
Ta có : \(\widehat {QON} = \widehat {MOP} = 50^\circ \) ( 2 góc đối đỉnh)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\) ( 2 góc kề bù)
\(\widehat {MOP} + \widehat {PON} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 50^\circ + \widehat {PON} = 180^\circ \\ \Rightarrow \widehat {PON} = 180^\circ - 50^\circ = 130^\circ \end{array}\)
Vì OK là tia phân giác của \(\widehat {PON}\)
\( \Rightarrow \widehat {POK} = \widehat {NOK} = \frac{1}{2}.\widehat {PON} = \frac{1}{2}.130^\circ = 65^\circ \)
Vậy khẳng định A, C, D đúng, B sai
Hướng dẫn giải:
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc

