Câu hỏi:
2 năm trước
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {70^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
Trả lời bởi giáo viên
Đáp án đúng: a
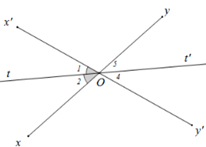
Vì \(Ot\) là tia phân giác của góc \(xOx'\) nên \(\widehat {xOt} = \widehat {tOx'} = \frac{1}{2}\widehat {xOx'} = \frac{1}{2}{.70^o} = {35^o}\)
Vì \(Oy\) là tia đối của \(Ox,Ot'\) là tia đối của \(Ot\)
\( \Rightarrow \widehat {yOt'} = \widehat {xOt} = {35^o}\) (tính chất hai góc đối đỉnh).
Hướng dẫn giải:
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc

