Cho tam giác \(ABC\) cân tại đỉnh \(A\) với \(\widehat A < {90^0}\). Kẻ \(BD \bot AC\) tại \(D.\) Trên cạnh \(AB,\) lấy điểm \(E\) sao cho \(AE = AD.\) Chọn câu sai.
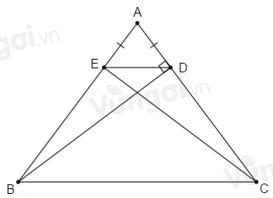
Do tam giác ABC cân tại \(A\) nên \(\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2}\) (1)
Ta thấy \(\Delta ADE\) có: \(AD = AE\,\,(gt)\) nên \(\Delta ADE\) cân tại \(A\).
\( \Rightarrow \widehat {AED} = \dfrac{{{{180}^0} - \widehat A}}{2}\) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat {AED}\). Mặt khác hai góc này ở vị trí đồng vị nên \(DE//BC.\)
Vậy A đúng.
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat A\) chung
\(AD = AE\,(gt)\)
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\( \Rightarrow \Delta ABD = \Delta ACE\,(c.g.c)\)
\( \Rightarrow \widehat {ADB} = \widehat {AEC} = {90^o}\) (hai góc tương ứng).
Do đó \(\Delta ACE\) là tam giác vuông.
Cho tam giác \(ABC\) có \(\widehat A = \widehat B = \widehat C = {60^0}\). Khi đó:
Tam giác \(ABC\) có: \(\widehat A = \widehat B = \widehat C = {60^0}\) nên \(\Delta ABC\) là tam giác đều.
Tam giác đều cũng là một tam giác cân nên \(\Delta ABC\) là tam giác cân tại \(A,\,B,\,C.\)
\(\widehat A = \widehat B = \widehat C = {60^0}\) do đó tam giác \(ABC\) có ba góc đều là góc nhọn nên là tam giác nhọn.
Vậy cả A, B, C đều đúng.
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM > \dfrac{{BC}}{2}\). Chọn câu đúng.
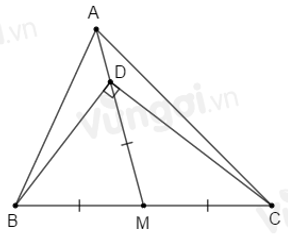
Trên tia \(MA\) lấy điểm \(D\) sao cho: \(MD = \dfrac{{BC}}{2}\), khi đó \(D\) nằm giữa \(A\) và \(M.\)
Ta có: \(\widehat {BDM}\) là góc ngoài đỉnh \(D\) của \(\Delta ABD\) nên \(\widehat {BDM} = \widehat {BAD} + \widehat {ABD}\) suy ra \(\widehat {BDM} > \widehat {BAD}\) (1)
\(\widehat {CDM}\) là góc ngoài đỉnh \(D\) của \(\Delta ACD\) nên \(\widehat {CDM} = \widehat {CAD} + \widehat {ACD}\) suy ra \(\widehat {CDM} > \widehat {CAD}\) (2)
\(\Delta BMD\) có: \(MB = MD\)(theo cách dựng) nên \(\Delta BMD\) cân tại \(M\), suy ra \(\widehat {MBD} = \widehat {BDM}\)
\(\Delta CMD\) có: \(MC = MD\) (theo cách dựng) nên \(\Delta CMD\) cân tại \(M\), suy ra \(\widehat {MCD} = \widehat {CDM}\)
Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta BDC\), ta có:
\(\widehat {CBD} + \widehat {BDC} + \widehat {BCD} = {180^o}\)
\( \Rightarrow \widehat {CBD} + \widehat {BDM} + \widehat {CDM} + \widehat {BCD} = {180^o}\)
\( \Rightarrow 2\widehat {BDM} + 2\widehat {CDM} = {180^o}\)
\( \Rightarrow 2\left( {\widehat {BDM} + \widehat {CDM}} \right) = {180^o}\)
\( \Rightarrow 2\widehat {BDC} = {180^o}\)
\( \Rightarrow \widehat {BDC} = \dfrac{{{{180}^o}}}{2} = {90^o}\) (3)
Từ (1), (2) và (3) ta có:
\(\widehat {BAD} + \widehat {CAD} < \widehat {BDM} + \widehat {CDM}\)
\( \Rightarrow \widehat {BAC} < \widehat {BDC}\)
\( \Rightarrow \widehat {BAC} < {90^o}\).
Tính số đo góc \(\widehat {MAN.}\)
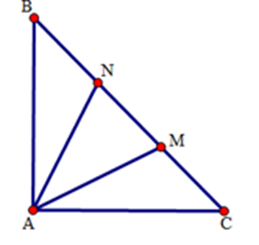
Xét tam giác $AMN,$ ta có:
\(\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) \)\(= {180^0} - {135^0} = {45^0}.\)
Vậy \(\widehat {MAN} = {45^0}.\)
Tam giác \(AMN\) là tam giác gì?
Do tam giác $ABC$ vuông cân ở $A$ nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác $AMB$ có: $BM = BA(gt),$ nên tam giác $AMB$ cân ở $B.$
Do đó $\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2}$$ = \dfrac{{{{180}^0} - {{45}^0}}}{2} = {67^0}30'$
Chứng minh tương tự ta được tam giác $ANC$ cân ở $C$ và \(\widehat {ANC} = {67^0}30'\).
Xét tam giác $AMN$ có: \(\widehat {AMN} = \widehat {ANM} = {67^0}30'\), do đó tam giác $AMN$ cân ở $A.$
Tam giác \(AMN\) là tam giác gì?
Do tam giác $ABC$ vuông cân ở $A$ nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác $AMB$ có: $BM = BA(gt),$ nên tam giác $AMB$ cân ở $B.$
Do đó $\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2}$$ = \dfrac{{{{180}^0} - {{45}^0}}}{2} = {67^0}30'$
Chứng minh tương tự ta được tam giác $ANC$ cân ở $C$ và \(\widehat {ANC} = {67^0}30'\).
Xét tam giác $AMN$ có: \(\widehat {AMN} = \widehat {ANM} = {67^0}30'\), do đó tam giác $AMN$ cân ở $A.$
Tam giác \(ABC\) có \(\widehat A = 45^\circ ;\,\widehat B - \widehat C = 35^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
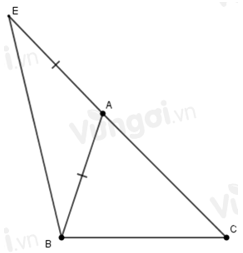
Xét tam giác \(ABC\) có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc của tam giác) và \(\widehat A = 45^\circ ;\,\widehat B - \widehat C = 35^\circ \,\left( {gt} \right)\)
Suy ra \(\widehat B + \widehat C = {180^o} - \widehat A = {180^o} - {45^o} = 135^\circ \)
Suy ra \(\widehat B = \dfrac{{135^\circ + 35^\circ }}{2} = 85^\circ ;\,\widehat C = {135^o} - {85^o} = 50^\circ \)
Xét tam giác \(AEB\) cân tại \(A\) (do \(AB = AE\,\left( {gt} \right)\)) nên \(\widehat {AEB} = \widehat {ABE}\) (tính chất tam giác cân) (1)
Lại có: \(\widehat {BAC}\) là góc ngoài tại đỉnh \(A\)của tam giác \(AEB \Rightarrow \widehat {BAC} = \widehat {AEB} + \widehat {ABE}\) (2)
Từ (1) và (2) suy ra: \(\widehat {ABE} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{45}^o}}}{2} = {22^o}30'\)
Do đó \(\widehat {CBE} = \widehat {CBA} + \widehat {ABE} = 85^\circ + 22^\circ 30' = 107^\circ 30'.\)
Chọn câu đúng.
Tam giác đều là tam giác có ba cạnh bằng nhau. Trong tam giác đều, ba góc bằng nhau và cùng bằng \({60^0}\) (A đúng; D sai).
Tam giác cân là tam giác có hai cạnh bằng nhau (B sai).
Tam giác vuông cân là tam giác cân có góc ở đỉnh bằng \({90^o}\) nên tam giác vuông cân không phải tam giác đều (C sai).
Cho tam giác \(ABC\) có: \(\widehat B = \widehat C = {45^0}.\) Khi đó tam giác \(ABC\) là tam giác gì?
Chọn kết luận đúng nhất:
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\), ta có:
\(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat A = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - \left( {{{45}^o} + {{45}^o}} \right) = {90^o}\)
\(\Delta ABC\) có \(\widehat A = {90^o};\,\widehat B = \widehat C = {45^o}\) nên \(\Delta ABC\) là tam giác vuông cân.
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = 2\alpha.\) Tính góc \(B\) theo \(\alpha.\)
Do tam giác ABC cân tại \(A\) nên \(\widehat B = \widehat C\).
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\), ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)
\( \Rightarrow \widehat B + \widehat C = {180^0} - \widehat A\)
\( \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - 2\alpha }}{2} = {90^o} - \alpha \).
Một tam giác cân có góc ở đỉnh bằng \({46^0}\) thì số đo góc ở đáy là:
Sử dụng cách tính số đo góc ở đáy của tam giác cân ta có:
Số đo góc ở đáy bằng: \(\dfrac{{{{180}^0} - {{46}^0}}}{2} = {67^0}.\)
Một tam giác cân có góc ở đáy bằng \({52^0}\) thì số đo góc ở đỉnh là:
Tổng số đo hai góc ở đáy là: \({52^o}.2 = 104^\circ \)
Vì tổng ba góc của tam giác bằng \(180^\circ \) nên số đo góc ở đỉnh tam giác cân là:
\(180^\circ - 104^\circ = 76^\circ .\)
Trong hình vẽ dưới đây có:
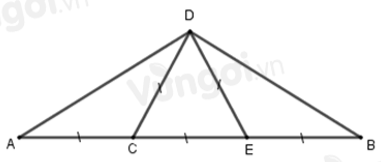
Từ hình vẽ ta có: \(DC = CE = ED = EB = CA\).
Vì \(DC = CE = ED\) nên \(\Delta CDE\) là tam giác đều.
Vì \(DC = CA\) nên \(\Delta ACD\) cân tại \(C.\)
Vì \(ED = EB\) nên \(\Delta BED\) cân tại \(E.\)
\(\Delta CDE\) là tam giác đều nên \(\widehat {DCE} = \widehat {DEC} = {60^o}\).
Ta có: \(CA = EB\)
\( \Rightarrow CA + CE = EB + CE\)
\( \Rightarrow AE = BC\)
Xét \(\Delta ADE\) và \(\Delta BDC\) có:
\(DE = DC\,(gt)\)
\(AE = BC\,(cmt)\)
\(\widehat {DEA} = \widehat {DCB} = {60^o}\)
\( \Rightarrow \Delta ADE = \Delta BDC\,(c.g.c)\)
\( \Rightarrow DA = DB\) (hai cạnh tương ứng).
\(\Delta ADB\) có \(DA = DB\) (cmt) nên \(\Delta ADB\) cân tại \(D\).
Vậy hình vẽ có 1 tam giác đều và 3 tam giác cân.
Tính số đo \(x\) trên hình vẽ sau:
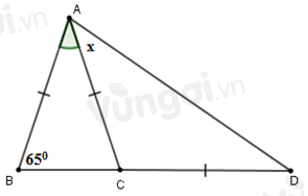
Tam giác \(ABC\) cân tại \(A\) (vì \(AB = AC\) ) nên \(\widehat B = \widehat {ACB} = {65^o}\).
\(\widehat {ACB} + \widehat {ACD} = {180^o}\) (hai góc kề bù)
\( \Rightarrow \widehat {ACD} = {180^o} - \widehat {ACB} = {180^o} - {65^o} = {115^o}.\)
Tam giác \(ACD\) cân tại \(C\) (vì \(CA = CD\)) và \(\widehat {ACD} = {115^o}\) nên \(\widehat {CAD} = \dfrac{{{{180}^o} - \widehat {ACD}}}{2} = \dfrac{{{{180}^o} - {{115}^o}}}{2} = {32^o}30'\)
Vậy \(x = {32^o}30'.\)
Tính số đo góc \(\widehat {MAN.}\)
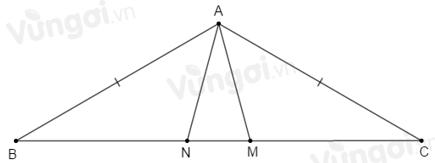
Sử dụng kết quả câu trước \(\Delta AMN\) cân tại \(A\) có: \(\widehat {AMN} = \widehat {ANM} = {75^o}\).
\( \Rightarrow \widehat {MAN} = {180^0} - 2\widehat {AMN} = {180^0} - {2.75^0} = {30^0}\).
Vậy \(\widehat {MAN} = {30^0}.\)
Tam giác \(AMN\) là tam giác gì?
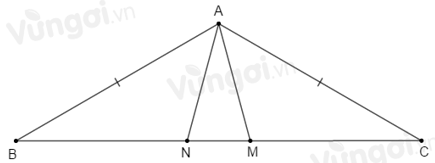
\(\Delta ABC\) cân ở \(A\) nên \(\widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{120}^o}}}{2} = {30^0}\).
Xét \(\Delta AMB\) có: BM = BA(gt) nên \(\Delta AMB\) cân ở \(B.\)
Do đó \(\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^o}\)
Xét \(\Delta ANC\) có: \(CN = CA\) (vì cùng bằng \(AB\)) nên \(\Delta ANC\) cân ở \(C\).
Do đó \(\widehat {ANC} = \dfrac{{{{180}^0} - \widehat C}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^o}\).
Xét \(\Delta AMN\) có: \(\widehat {AMN} = \widehat {ANM} = {75^o}\), do đó \(\Delta AMN\) cân ở \(A.\)
Tam giác \(AMN\) là tam giác gì?

\(\Delta ABC\) cân ở \(A\) nên \(\widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{120}^o}}}{2} = {30^0}\).
Xét \(\Delta AMB\) có: BM = BA(gt) nên \(\Delta AMB\) cân ở \(B.\)
Do đó \(\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^o}\)
Xét \(\Delta ANC\) có: \(CN = CA\) (vì cùng bằng \(AB\)) nên \(\Delta ANC\) cân ở \(C\).
Do đó \(\widehat {ANC} = \dfrac{{{{180}^0} - \widehat C}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^o}\).
Xét \(\Delta AMN\) có: \(\widehat {AMN} = \widehat {ANM} = {75^o}\), do đó \(\Delta AMN\) cân ở \(A.\)
Tam giác \(AMN\) là tam giác gì?
Do tam giác $ABC$ vuông cân ở $A$ nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác $AMB$ có: $BM = BA(gt),$ nên tam giác $AMB$ cân ở $B.$
Do đó $\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2}$$ = \dfrac{{{{180}^0} - {{45}^0}}}{2} = {67^0}30'$
Chứng minh tương tự ta được tam giác $ANC$ cân ở $C$ và \(\widehat {ANC} = {67^0}30'\).
Xét tam giác $AMN$ có: \(\widehat {AMN} = \widehat {ANM} = {67^0}30'\), do đó tam giác $AMN$ cân ở $A.$
Chọn câu sai.
Tam giác đều là tam giác có ba cạnh bằng nhau.
Trong tam giác đều, mỗi góc bằng \({60^0}.\)
Nên A, B đúng.
Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều vì nó chỉ có hai cạnh bên bằng nhau.
Vậy C sai.
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Mỗi góc nhọn của tam giác vuông cân bằng \({45^0}.\)

