Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

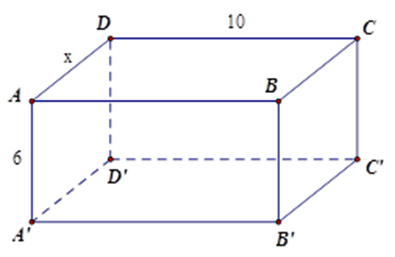
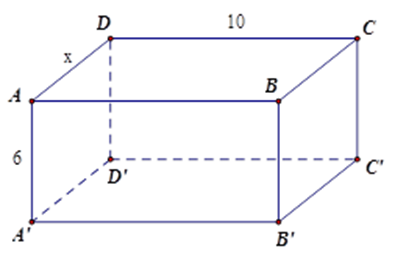
Đặt $AD = x$ .

Diện tích xung quanh bằng:

$2\left( {10 + x} \right).6\left( {c{m^2}} \right)$

Tổng diện tích hai đáy bằng  $2.10x\left( {c{m^2}} \right)$

Ta có $2\left( {10 + x} \right).6{\rm{ }} = {\rm{ }}2.10x \Leftrightarrow 60 + 6x = 10x \Leftrightarrow x = 15$

Kích thước còn lại của đáy bằng $15cm$ .

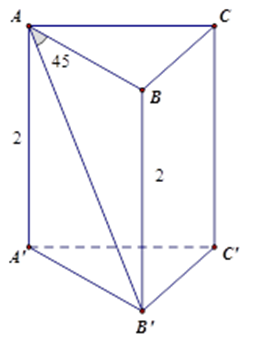
Tam giác vuông $ABB'$  có \(\widehat {BAB'} = {45^0}\) nên là tam giác vuông cân tại \(B\) nên $AB = BB' = 2cm$ .

Vì tam giác \(ABC\) đều nên chu vi đáy bằng $3AB = 3.2 = 6cm$

Diện tích xung quanh bằng $6.2 = 12\left( {c{m^2}} \right).$

Gọi $a$  và $b$  là các kích thước của đáy.

Ta có $V = 6ab$ nên $V$  lớn nhất \( \Leftrightarrow \) $ab$  lớn nhất

\({S_{xq}} = 120\) nên \(2\left( {a + b} \right).6 = 120\) hay \(a + b = 10\).

Ta có: \(ab = a\left( {10 - a} \right) =  - {a^2} + 10a =  - {\left( {a - 5} \right)^2} + 25 \le 25\).

Suy ra \(V = 6ab \le 6.25 = 150\).

Thể tích lớn nhất bằng \(150\) \({\rm{c}}{{\rm{m}}^3}\) khi \(a = b = 5\), tức là các cạnh đáy bằng $5$ cm.

Vì đáy là tam giác vuông nên diện tích đáy \(S = \dfrac{{8.10}}{2} = 40\,cm\) .

Thể tích lăng trụ đứng là \(V = S.h = 40.20 = 800\,c{m^3}\) .

Công thức tính thể tích hình lăng trụ đứng là: $V = S.h$

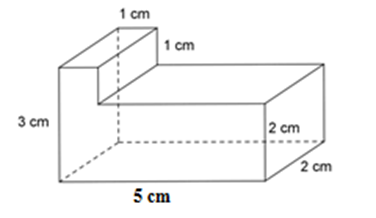
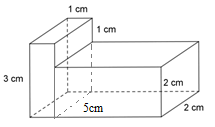
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là

\(3cm,\;\;1cm,\;\;2cm;\)  hình hộp chữ nhật thứ hai có kích thước là \(2cm,\;\;4cm,\;\;2cm.\)

Thể tích hình hộp chữ nhật thứ nhất là:   \({V_1} = 3.1.2 = 6\;c{m^3}\)

Thể tích hình hộp chữ nhật thứ hai là:  \({V_2} = 2.4.2 = 16\;c{m^3}\)

Thể tích hình lăng trụ đứng là:  \(V = {V_1} + {V_2} = 6 + 16 = 22\;c{m^3}\)

Diện tích xung quanh \({S_{xq}} = 2.(8 + 3).2 = 44\;c{m^2}\)

Thể tích của hình lăng trụ đứng là:\(V = 8.3.2 = 48\;c{m^3}\)