Chứng minh định lý là
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Trong các câu sau, câu nào cho một định lí
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
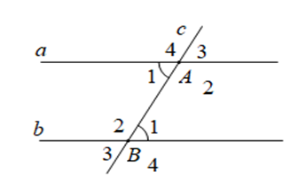
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
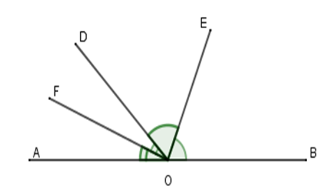
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} + \widehat {{B_2}} = 180^\circ \) (tham khảo hình vẽ) là của định lý nào dưới đây?
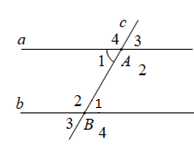
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Phát biểu định lý sau bằng lời:
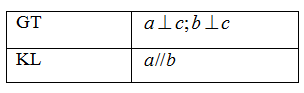
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Định lý sau được phát biểu thành lời là:
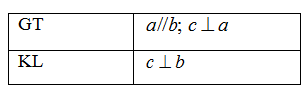
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn câu đúng.
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra

